金融物理學
出自 MBA智库百科(https://wiki.mbalib.com/)
金融物理學(Financial Physics)
目錄 |
什麼是金融物理學[1]
金融物理學是用統計物理、理論物理、複雜系統理論、非線性科學、應用數學等的概念、理論和方法研究金融市場,通過自組織而涌現的巨集觀規律及其複雜性的一門新興交叉學科。簡而言之,金融物理學家將金融市場看作一個複雜系統,其中的各種數據(如個股價格、指數、房價等)看作是物理實驗數據,力圖尋找和闡釋其中的物理規律。
金融物理學的主要研究內容[1]
金融物理學的主要研究內容包括四個方面,其中的大部分內容在本書的後續章節會進行深入介紹。需要指出的是,中國科學技術大學的李平等人也給出了一個十分類似的分類(李平、汪秉巨集、全巨集俊:《金融物理的若幹問題與研究進展(I):價格的統計分析與價格漲落的隨機過程模擬》,《物理》,2004,33(1):28~33)。
第一,金融市場變數(包括收益率、波動率等)的統計規律,特別是金融市場中涌現的具有普適性的標度律,其中最基本的性質是關於收益率的尖峰胖尾分佈。
第二,證券的相關性、極端事件、金融風險管理和投資組合等。分形市場假說研究相關變數(特別是收益率)的長期記憶性,或自相關性,認為價格演化中存在自相似結構。多重分形理論和方法也被廣泛應用於金融市場時間序列的分析。
第三,巨集觀市場的建模和預測,包括用隨機過程對收益率建模和對數周期性冪律模型等。對數周期性冪律模型是基於交易者之間的相互模仿,這些局部相互作用可形成正反饋,從而導致泡沫和反泡沫的產生,因此可用於金融泡沫和反泡沫的建模和預測。對數周期性冪律模型可分為兩大類,即維爾斯特拉斯族模型和朗道族模型。
第四,金融市場的微觀模型,主要包括基本面投資者和雜訊交易者博弈、逾滲模型(Percolation Models)、伊辛模型(Ising Models)、少數者博弈模型(Minority Games)等,以及由此而衍生出來的各種模型。通過對微觀模型的模擬研究,可以深入瞭解金融市場的微觀結構和價格形成機制。
金融物理學的研究專題[2]
一、概率分佈
概率分佈是金融市場變數的最本質也是最重要的統計性質,特別是收益率的概率分佈,在各種資產定價模型中處於核心地位。鑒於概率密度函數、特征函數和矩函數之間的等價變換關係,金融變數高階矩可能呈現的標度不變性和多重分形特性,反映了其概率分佈的標度不變性。
1900年,Bachelier首次應用布朗運動來描述股票價格演化。20世紀前半葉,一些學者對布朗運動模型進行了理論和實證研究,但是由於計算能力的限制,所得結論的統計意義並不顯著。1959年,Osborne發表論文指出,1955~1956年在紐約證交所交易的上千隻股票的月度收益率和年度收益率以及道瓊斯指數在1916-56年期間的月度收益率都服從高斯分佈,他還用更多的數據來驗證布朗運動模型。Fama將之稱為Bachelier-Osbome模型。
1963年,Mandelbrot創造性地應用帕雷托定律描述投機市場價格收益率的尾分佈,隨後指出平穩帕雷托分佈可以比高斯分佈更好地刻劃棉花價格波動的概率分佈,徹底顛覆了布朗運動模型,並引起了經濟學界的極大關註。1995年,Mantegna和Stanley將截尾列維分佈用於S&P 500指數高頻數據的建模,發現收益率在6個方差範圍內可以用列維分佈很好擬合。可以說,Mantegna和Stanley發表於1995年的這一開創性工作,正式拉開了金融物理學研究的大幕,吸引了大批物理學家加入到相關研究中來。
1998年,Gopikrishnan等人分析了美國股市的個股和指數的收益率(時間間隔從5分鐘至120分鐘),發現其尾分佈具有冪律形式,正尾指數略大於負尾指數,其值都接近-3,被稱為負三次方定律。近幾年來,很多論文報道了各種不同金融市場中的不同變數服從負三次方定律或冪律尾分佈,然而令人擔憂的是,其中有些結論是基於很窄的無標度區,是不可靠的。事實上,對有些情形採用拉伸指數分佈更為合適。
收益率分佈的“尖峰胖尾”形態可從不同時間間隔時的概率密度演化的角度來體現。描述概率密度在不同尺度下的演化規律的方法很多,比如湍流研究中的變分理論,它假設收益率的概率密度是給定方差收益率的概率密度的線性疊加,即
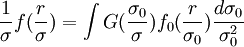
式中f是方差為σ標準化收益率r / σ的概率密度,f0是方差為σ0標準化收益率r / σ0的概率密度,G為σ的概率密度函數。這一概率密度演化模型和有限方差從屬模型和混合正態模型在有相通處,在描述金融市場收益率演化和間歇性方面十分成功。
二、相關性與分形市場假說
有效市場假說是金融市場研究的一個重要概念,其核心思想是,任何時刻證券的價格都完全並正確地反映了所有可獲取的信息。換言之,市場的價格波動,取決於投資者的對未來收益率的預期。市場有效性的基本假設是證券存在一個客觀的均衡價值,其價格已反映所有已知的信息,並且總是趨於均衡價值。這一假設意味著市場中的投資者是理性的經濟人,其買賣的理性決策行為將使證券的價格趨向其內在價值,而價格趨向均衡的速度依賴於信息的可利用性和市場的競爭性。
在弱式有效市場中,價格的變化無法通過歷史收益率進行預測,即價格變動是隨機的,因此對弱式有效市場的檢驗主要側重於檢驗收益率時間序列是否存在自相關性,或長期記憶性,其中最常用的是隨機游走模型。技術交易者的一個基本理念是,歷史總是不斷重覆的,價格時間序列中存在各種各樣的價格模式,只要識別出這些模式,就可能戰勝市場獲取超額利潤。而在弱式有效的市場中,價格波動不具記憶性。隨機游走模型可追溯到1900年Bachelier的工作,1933年Cowles三世開始了早期實證研究,而Samuelson在1967年的論文則明確指出價格波動是隨機的。
1970年,Mandelbrot提出用R/S分析研究證券收益率,認為價格時間序列具有長程相關性u引心1。1991年,Lo給出了修正R/S分析,用於對R/S分析的結果進行統計檢驗,並指出許多霍斯特指數大於0.5的價格時間序列的長期記憶性並不顯著,此後的實證研究大多支持Lo的結論。1999年,Teverovsky等人指出,Lo的修正R/S分析傾向於過度拒絕長期記憶性,然而這一研究並未受到研究者的應有重視。
三、多重分形特性
最早用多重分形理論分析金融時問序列的學者可能是Ghashghme等人,他們將外匯市場與湍流類比,發現美元和德國馬克外匯價格波動的矩函數具有非線性的標度律,而其他關於匯市多重分形特性的實證研究也得到了廣泛關註。多重分形特性在其他金融時間序列中也有大量報道,如黃金價格、商品價格、股票個股價格、股市指數等。在大量實證研究報道金融市場價格序列的多重分形特性的同時,也出現了不少多重分形模型用來描述這個特性。
然而,大部分文獻只熱衷於報道實證研究的結果,卻忽略了更本質的內容,即產生多重分形特性的原因。研究表明,即使是一個不具多重分形特性的分形模型,也可能產生所謂的多重分形性質舊引。
因而這些實證得到的多重分形特性,更確切的表述應該是“經驗多重分形特性”。時間序列中的經驗多重分形特性有兩個可能的來源,一是波動性中存在的長程相關性,二是收益率的胖尾分佈曙利。對很多金融時間序列,經驗多重分形特性源於胖尾分佈的零假設無法拒絕口引,這一結論已經為一些研究所證實,而部分金融時間序列的多重分形譜具有很窄的奇異性分佈,進一步為之提供了佐證。這些問題指出,需要用更堅實有效的方法更深入地研究金融市場中的多重分形特性。
四、金融市場的微觀模型
為了理解金融市場交易者行為對形成市場巨集觀規律影響,可以構建並研究各種不同的微觀模型。模型市場的基本元素是經紀人,市場運行的規則既可以是基於經紀人的局部相關作用,也可以是受全局因素影響,或者是兩者的疊加,這些模型能夠產生部分程式化性質。對於部分程式化規律可能存在爭議,但對微觀模型而言,如果得到的價格時間序列具有與實際時間序列相同的程式化規律,則可認為該微觀模型在某些方面抓住了實際市場的屬性。基於經紀人的微觀模型主要包括四類:
第一類,基本面交易者和雜訊交易者博弈。根據交易定價策略的不同,金融市場中的交易者大致可以分為兩類,一部分交易者屬於基本面分析學派,認為資產股票的實際價格在偏離基礎價格後必然將回覆到基礎價格,而另一部分交易者則信奉技術分析,屬於技術分析交易者或圖形交易者,他們通過對價格走勢和模式的分析來確定投資策略。在微觀市場模型的研究中,雜訊交易者通常用來指稱技術分析者,在所構建的模型市場中,基本面交易者和雜訊交易者相互轉化,從而形成市場價格。1997年Bak等人提出的擴散反應模型晗鯽和1999年提出的Lux-Marchesi模型即屬於此類。
第二類,逾滲模型。這類模型最早由Cont和Bouchaud提出(CB模型),認為羊群行為是收益率胖尾分佈的微觀機理。該模型不考慮外界因素對交易者的影響,交易者之間通過局部相互影響,產生一個個簇,每個簇內的交易者採取相同的交易策略。Stauffer發現,CB模型屬於高維逾滲模型,是靜態的。Eguiluz和Zimmermann提出的EZ模型,是CB模型的一個動態推廣,通過信息傳播和羊群效應產生與CB模型一致的冪律尾分佈,拋棄了CB模型需要在臨界點附近演化的人為規定。EZ模型及其部分衍生模型可寫出演化方程並求解。
第三類,自旋模型。其中,伊辛模型中的經紀人具有買和賣兩種狀態,而帕茲模型則包含買、賣和觀望三種狀態。
第四類,少數者博弈模型。在各種微觀模型,最引人註目並被廣泛研究的模型,當數Challet和Zhang在1997年提出的少數者博弈模型,該模型基於Arthur提出的“酒吧問題”,用來描述適應經紀人對有限資源的競爭,其中的少數者獲勝。
五、金融市場的巨集觀模型
對數周期性冪律模型是基於交易者之間的相互模仿,這些局部相互作用可形成正反饋,從而導致泡沫和反泡沫的產生,因此可用於金融泡沫和反泡沫的建模和預測。對數周期性冪律模型可分為兩大類:維爾斯特拉斯族模型和朗道族模型,前者可以通過重整化群方法導出,而後者則是在臨界點附近的各級朗道展開近似。
對數周期性冪律模型在股市中的應用,最早在1995年由兩個小組獨立提出,併在泡沫湮沒時間預測和反泡沫走勢預測方面取得了不少成功,如日本日經指數反泡沫、英國房地產泡沫、中國股市反泡沫等。
評論(共6條)
感覺很虛 整篇都是中式的吹捧的風格 這麼厲害 怎麼從沒在公共上聽說過
更新新的內容,希望對您有幫助!
該詞條混淆了 Econophysics和financial physics。第1節和第3節講的是Econophysics,第2節和第4節講的是financial physics。而這兩個不是一個概念。前者是將物理學理論應用到金融學領域,解決經濟問題。而後者是通過對金融學本事的物理性質進行研究! 望得到修改!
謝謝指正!確實存在不同。已將經濟物理學獨立出來介紹。
MBA智庫百科是可以自由參與的百科,如有發現錯誤和不足,您也可以參與修改編輯,點擊條目上方的編輯進入即可參與,期待您的加入!~








看了,滿篇文章給人一種大海的感覺!