對數周期性冪律模型

出自 MBA智库百科(https://wiki.mbalib.com/)

對數周期性冪律模型(Log-Periodic Power Law模型;LPPL模型)

　　對數周期性冪律模型是基於交易者之間的相互模仿，這些局部相互作用可形成正反饋，從而導致泡沫和反泡沫的產生，因此可用於金融泡沫和反泡沫的建模和預測。對數周期性冪律模型可分為兩大類:維爾斯特拉斯族模型和朗道族模型，前者可以通過重整化群方法導出，而後者則是在臨界點附近的各級朗道展開近似。

　　對數周期性冪律模型在股市中的應用，最早在1995年由兩個小組獨立提出，併在泡沫湮沒時間預測和反泡沫走勢預測方面取得了不少成功，如口木口經指數反泡沫、英國房地產泡沫、中國股市反泡沫等。

　　一是對數周期性振蕩，線上性尺度下，越接近臨界時間，振蕩頻率越快，但在對數尺度下，振蕩頻率為常數;

　　二是冪律增長，或稱超指數增長，即價格的增長率不是常數，而是單調遞增。

　　1.不斷變化樣本數據起始點tstart與終止點tend，從而形成樣本數據系列（tstart，tend）。對於每一個樣本系列，我們可得到LPPL模型參數的估計值（A，B，C，tc，m,ω,φ）。為了確保每一系列樣本點以及估計的數量足夠多，我們每隔=5個交易日變換一次tstart及tend，同時確保tend與tstart的間隔不低於100個交易日。

　　2.給出tc的置信區間（20，80），從而判斷泡沫破裂的可能時間點。

　　3.畫出10條均方差最小的模擬路徑，即我們認為未來最有可能發生的路徑。

　　LPPL模型中共有7個參數需要估計，即（A，B，C，tc，m,ω,φ），其中4個非線性參數（tc，m,ω,φ），三個線性參數（A，B，C）。為了降低參數擬合的數量，同時也為了確保參數估計的穩定性，我們可以將線性參數表示成非線性參數估計值的表達式，從而只需估計非線性參數即可。我們可以將LPPL模型簡化為

　　ln p(t)=A+Bf(t)+Cg(t)

　　則線性參數（A，B，C）可以通過如下方程來求解：

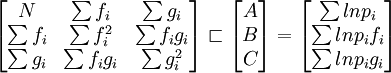
　　至於非線性參數的估計，我們只需利用非線性最優化求解即可。