漏斗實驗

出自 MBA智库百科(https://wiki.mbalib.com/)

漏斗實驗(Funnel Experiment)

　　在戴明博士四日談中，以漏斗實驗來解釋管理與干預問題。管理人員常因缺乏對系統變異的統計思考方式而對系統進行干預，造成問題越變越離譜。譬如，廠內的管理階層在品質會議中要求不良率最高的單位提出改善計劃或業務會議中要求營業額退步的營業員提出對策。以前國中的導師每周對學生評分排名，對退步的學生給與嚴厲的指責警告(現在應該還是一樣)。但是以長期來看不良率依然有高有低；營業額每月仍是有好有壞；學生的排名每周還是有進有退，這些數據的變異很多是系統的正常變異，也就是所謂共同原因的變異。但是，管理人員對這些變異進行干預，採取矯正措施，使得系統越變越複雜。例如，製程管理人員隱藏不良品使不良率好看；營業人員虛報營業額使得帳面上好看；學生到補習班先練習考試題目使得排名進步。以上這些現象在我們所處的工作或生活環境中屢見不鮮，我們應該先瞭解系統的變異是來自特殊原因或是共同原因，再採取適當的行動。

　　所謂漏斗實驗，就是假想我們有一漏斗，裝在桌上約半公尺高的架上，桌上有個靶。假設我們把一顆彈珠放入漏斗，不論我們放下的方式如何，彈珠就會以隨機的方式滾下漏斗，然後由漏斗底部掉下到靶上，再用鉛筆在落點做個記號。我們利用一些簡單的規則來使漏斗瞄準目標，這些規則相當於我們在使用設備、流程或系統中作的一些決策規則。

　　漏斗實驗的四種規則：

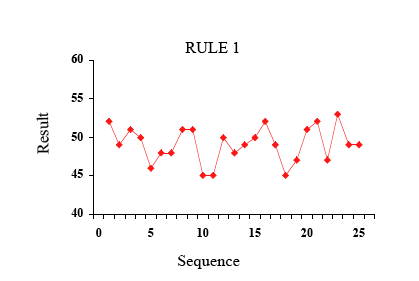
　　規則一：每次都不調整漏斗位置(結果：彈珠落點隨機分佈在目標值兩側)

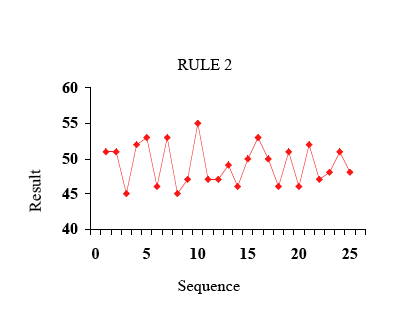
　　規則二：根據上一次落點，調整漏斗位置(結果：彈珠落點範圍較規則一大了約41%)

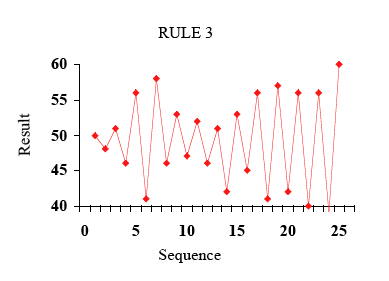
　　規則三：調整前先歸回目標值(結果：彈珠落點由兩側大幅散開)

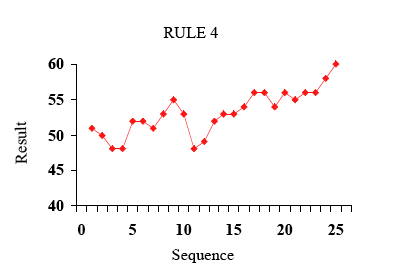
　　規則四：瞄準上一次的落點(結果：彈珠落點呈隨機漫步到天邊)

　　將四個規則模擬的結果繪在同張圖上，可以一目瞭然地比較四種規則的結果。

　　實驗材料：一個漏斗、一粒可以很容易通過漏斗的彈珠、一張桌子，最好鋪上桌布。

　　第一次實驗：規則為漏斗位置不變。首先在桌布上標出一點作為目標，開始實驗。將漏斗口瞄準目標點。保持這種狀態，將彈珠由漏斗口落下50次，在彈珠每次落下的靜止位置作標記。要求是將彈珠落到準確的一點上。

　　實驗的結果是得到近似圓形的點集，範圍遠遠超出我們的預期。儘管漏斗口一直都是對準目標點，但是彈珠有時很靠近目標點，下一次卻大大偏離目標點。

　　第二次實驗：規則為反向調正漏斗位置。在每次彈珠落下後，調整漏斗的位置，讓下一次的結果靠近目標點。即根據每次彈珠落下的靜止位置與目標位置的差距，調整漏斗的位置，以彌補前次的誤差。比如彈珠停在目標點西南30釐米處，就將漏斗由現在位置往東北移30釐米。

　　結果比第一次固定漏斗位置的結果糟糕。落點所形成的圖形，其直徑的變異度比依第一次直徑的差異度大一倍。因此，依據第二次所形成的圖形，面積比依據第一次所得的結果大41%。

　　第三次實驗：規則為調正漏斗位置前先回歸原位。允許每次彈珠落下後調整漏斗位置，但以目標點作為移 動的參考點。先讓漏斗回歸原位，然後按照落點與目標點的差距，把漏斗從原位調整到與目標點等距但相反方向的地方，以消除前次偏誤。 這次實驗的結果更糟。彈珠的落點變得更不穩定，幅度越來越大，偶爾有幾次是幅度漸減，其後幅度又變大。

　　第四次實驗：規則為瞄準上次落點。在每次彈珠落下之後，就將漏斗移到該靜止點之上。 結果是落點向一個方向擴散，距離目標點越來越遠。

　　通過上述四個實驗，可以得出以下結論：

　　第一

　　第一次實驗中的規則是所有規則中最有效果的。但人們對第一次規則不滿，所以又進行了第二、三、四次改變規則的實驗。規則改變的思路是消除落點誤差，但結果會越來越差。現實管理中，用儀器測量零件，根據零件的誤差進行反向調整，就相當於規則二；根據上月的預算執行差異調整本月預算，就相當於規則三(防止核擴散、貿易壁壘、藥物干預，都屬於這一規則)；由老員工來訓練新員工，就相當於規則四(每生產一個產品都用上一個成品為樣本也屬於這一規則)。漏斗實驗告訴管理者，對於系統誤差的干預，只會增大下次的誤差。比如，我們根據財務資料做出調整決定，所看到的資料就相當於上次的彈珠落點。正確的做法是，保持第一次實驗的規則，改善系統。例如，這一漏斗系統可以做出兩種改善：第一，降低漏斗的高度。效果很好，落點形成的近似圓形半徑縮小。這樣做無需增加成本。第二，改用比較粗糙的桌布。這樣，彈珠滾動的距離就會縮短。成本只需一個桌布的價格。

　　第二

　　漏斗實驗強調的是管理人員必須利用統計的思考方式，以分辨製程系統的變異是共同原因造成或特殊原因造成。一有特殊原因，能夠立即發現而採取矯正措施。若製程系統祗有共同原因且變異太大，管理人員就須針對系統的關鍵因素，作基本上的改變，以有效改善系統。

　　第三

　　傳統的SPC手法就是有計畫的在製程系統收集數據，以簡單的管製圖分析驗證製程系統的變異是否有特殊原因存在或偵測是否有特殊原因存在。若有特殊原因存在，則須局部對策，發掘特殊原因，消除特殊原因，防止再發。並且持續監控製程系統，使製程系統保持穩定且可預測。

　　第四

　　當製程系統在統計的管制狀態下時，也就是製程系統保持穩定且可預測。此時評估製程系統的製程能力，才真正能估計其符合規格的能力，亦可為製程系統持續改善的依據。品質管理發展至今，SPC的變異理論已經普遍在業界推廣應用，只是很多人在用而不自知。譬如，ISO品質管理系統的建立、維護及稽核；品管圈活動步驟；福特汽車8D的改善程式；SIX SIGMA的活動程式。

　　規則一：一般可視為正確的管理方式，先對系統的變異進行解析，以分辨變異是來自特殊原因或共同原因。若有特殊原因，則進行局部對策，消除原因防止再發；若祇是系統的共同原因，則須由管理當局進行系統改善。

　　製程管制系統的目的是要經濟有效地管制產品或製程品質。也就是說，當製程系統只有共同原因時，不要過度去調整或干預製程；當製程系統有特殊原因出現時，不要忽略局部對策的機會。製程管制系統的功能是要使製程系統在統計的管制狀態下，使其變異只源自於系統的共同原因。以此來監控當特殊原因出現時能被察覺而給予局部對策，對產品或製程品質有不良影響的消除之，對產品或製程品質有益處的保留之。當製程系統在管制狀態下時，即穩定且可預測，進行製程系統的改善，才有實質的效益。

　　規則二：一般可視為系統在共同原因的變異下，對系統缺乏認識的作業及管理人員對系統進行干預，而使系統產生結構性的變化。除非系統本身被一些可預測的因素影向，規則二可以應用來調整系統使之變異減少。例如，冷氣機的自動調溫系統，隨著室溫的改變來調整冷風的量，使得室溫在設定的溫度上。MacGregor 曾撰文解釋在系統平均的變動可預測之下，規則二會較規則一的變異小。因此，解釋規則二時必須假設系統在共同原因的變異下。下列幾個實例說明之：

　　(1)自動化製程控制常以上一次製程測定的結果來調整製程；

　　(2)作業員以上一個工件的測定結果來調整補償與目標值的差距；

　　(3)老師以學生考試的分數差目標值幾分來決定處罰的輕重，使得程度差的學生自暴自棄；

　　(4)作菜時習慣先嘗嘗鹹淡，再加水或加鹽來中和鹹淡，使得每次作的菜鹹淡不一。

　　規則三：如規則二的補償式調整，惟調整時回到目標值再調整其差值。在系統祗有共同原因時，其變異較規則二的調整方法更大而且上下交替大幅變動。下列幾個實例說明之：

　　(1)自動化製程控制常以上一次製程測定的結果來調整製程，但以原設定補償性調整；

　　(2)作業員以上一個工件的測定結果來調整與目標值的差距，但以原設定補償性調整；

　　(3)業務員當月業績低於目標10萬元，下個月業績必須達到目標再加10萬。

　　(4)統獨意識形態，依民意或選票，反向調整施政。

　　(5)賭博輸錢或股票投資失利，加倍賭資或投資，希望把錢贏回來。

　　(6)公家機關本期預算沒用完，下期多用一點補回來，不發白不發。

　　規則四：這是最常見的干預模式，幾乎所有產業、政府及學術機構都可見到。下列幾個實例可以說明之：

　　(1)作業員以上一次的生產結果為標準，依樣畫葫蘆，而忘記原始的標準；

　　(2)工程變更時祗以上一版本為變更依據，而不追溯原始設計；

　　(3)教育訓練時老鳥帶新鳥或學長管學弟，造成訓練的結果與原意愈差愈遠；

　　(4)編製預算依上一期的結果乘上一個百分比為準，結果預算愈編愈大；

　　(5主持人給第一位表演者一個題目，表演給第二位表演者看，再由第二位表演給下一位看，依此類推，再由最後再一位表演者說出主持人給的題目是什麼，通常是牛頭不對馬嘴。

　　(6)語言的演化，例如，臺灣的閩南話或客家話與大陸、新馬閩南語或客家話有所差異。

• 紅珠實驗