漏斗实验

出自 MBA智库百科(https://wiki.mbalib.com/)

漏斗实验(Funnel Experiment)

　　在戴明博士四日谈中，以漏斗实验来解释管理与干预问题。管理人员常因缺乏对系统变异的统计思考方式而对系统进行干预，造成问题越变越离谱。譬如，厂内的管理阶层在品质会议中要求不良率最高的单位提出改善计划或业务会议中要求营业额退步的营业员提出对策。以前国中的导师每周对学生评分排名，对退步的学生给与严厉的指责警告(现在应该还是一样)。但是以长期来看不良率依然有高有低；营业额每月仍是有好有坏；学生的排名每周还是有进有退，这些数据的变异很多是系统的正常变异，也就是所谓共同原因的变异。但是，管理人员对这些变异进行干预，采取矫正措施，使得系统越变越复杂。例如，制程管理人员隐藏不良品使不良率好看；营业人员虚报营业额使得帐面上好看；学生到补习班先练习考试题目使得排名进步。以上这些现象在我们所处的工作或生活环境中屡见不鲜，我们应该先了解系统的变异是来自特殊原因或是共同原因，再采取适当的行动。

　　所谓漏斗实验，就是假想我们有一漏斗，装在桌上约半公尺高的架上，桌上有个靶。假设我们把一颗弹珠放入漏斗，不论我们放下的方式如何，弹珠就会以随机的方式滚下漏斗，然后由漏斗底部掉下到靶上，再用铅笔在落点做个记号。我们利用一些简单的规则来使漏斗瞄准目标，这些规则相当于我们在使用设备、流程或系统中作的一些决策规则。

　　漏斗实验的四种规则：

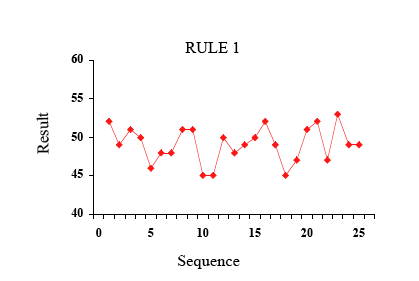
　　规则一：每次都不调整漏斗位置(结果：弹珠落点随机分布在目标值两侧)

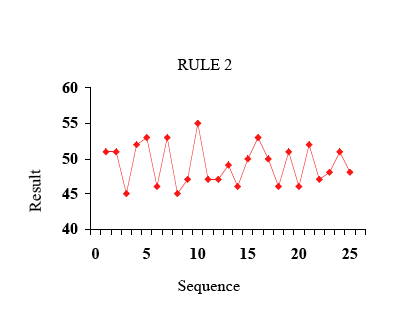
　　规则二：根据上一次落点，调整漏斗位置(结果：弹珠落点范围较规则一大了约41%)

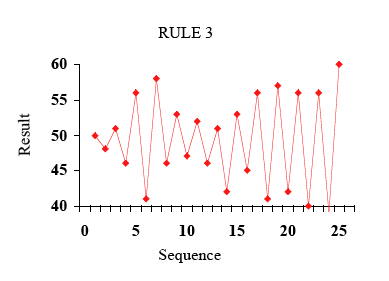
　　规则三：调整前先归回目标值(结果：弹珠落点由两侧大幅散开)

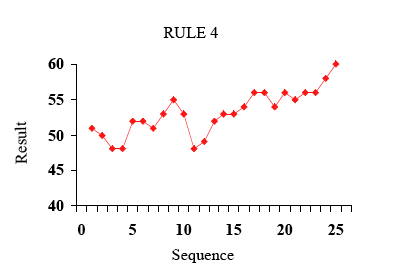
　　规则四：瞄准上一次的落点(结果：弹珠落点呈随机漫步到天边)

　　将四个规则仿真的结果绘在同张图上，可以一目了然地比较四种规则的结果。

　　实验材料：一个漏斗、一粒可以很容易通过漏斗的弹珠、一张桌子，最好铺上桌布。

　　第一次实验：规则为漏斗位置不变。首先在桌布上标出一点作为目标，开始实验。将漏斗口瞄准目标点。保持这种状态，将弹珠由漏斗口落下50次，在弹珠每次落下的静止位置作标记。要求是将弹珠落到准确的一点上。

　　实验的结果是得到近似圆形的点集，范围远远超出我们的预期。尽管漏斗口一直都是对准目标点，但是弹珠有时很靠近目标点，下一次却大大偏离目标点。

　　第二次实验：规则为反向调正漏斗位置。在每次弹珠落下后，调整漏斗的位置，让下一次的结果靠近目标点。即根据每次弹珠落下的静止位置与目标位置的差距，调整漏斗的位置，以弥补前次的误差。比如弹珠停在目标点西南30厘米处，就将漏斗由现在位置往东北移30厘米。

　　结果比第一次固定漏斗位置的结果糟糕。落点所形成的图形，其直径的变异度比依第一次直径的差异度大一倍。因此，依据第二次所形成的图形，面积比依据第一次所得的结果大41%。

　　第三次实验：规则为调正漏斗位置前先回归原位。允许每次弹珠落下后调整漏斗位置，但以目标点作为移 动的参考点。先让漏斗回归原位，然后按照落点与目标点的差距，把漏斗从原位调整到与目标点等距但相反方向的地方，以消除前次偏误。 这次实验的结果更糟。弹珠的落点变得更不稳定，幅度越来越大，偶尔有几次是幅度渐减，其后幅度又变大。

　　第四次实验：规则为瞄准上次落点。在每次弹珠落下之后，就将漏斗移到该静止点之上。 结果是落点向一个方向扩散，距离目标点越来越远。

　　通过上述四个实验，可以得出以下结论：

　　第一

　　第一次实验中的规则是所有规则中最有效果的。但人们对第一次规则不满，所以又进行了第二、三、四次改变规则的实验。规则改变的思路是消除落点误差，但结果会越来越差。现实管理中，用仪器测量零件，根据零件的误差进行反向调整，就相当于规则二；根据上月的预算执行差异调整本月预算，就相当于规则三(防止核扩散、贸易壁垒、药物干预，都属于这一规则)；由老员工来训练新员工，就相当于规则四(每生产一个产品都用上一个成品为样本也属于这一规则)。漏斗实验告诉管理者，对于系统误差的干预，只会增大下次的误差。比如，我们根据财务资料做出调整决定，所看到的资料就相当于上次的弹珠落点。正确的做法是，保持第一次实验的规则，改善系统。例如，这一漏斗系统可以做出两种改善：第一，降低漏斗的高度。效果很好，落点形成的近似圆形半径缩小。这样做无需增加成本。第二，改用比较粗糙的桌布。这样，弹珠滚动的距离就会缩短。成本只需一个桌布的价格。

　　第二

　　漏斗实验强调的是管理人员必须利用统计的思考方式，以分辨制程系统的变异是共同原因造成或特殊原因造成。一有特殊原因，能够立即发现而采取矫正措施。若制程系统祗有共同原因且变异太大，管理人员就须针对系统的关键因素，作基本上的改变，以有效改善系统。

　　第三

　　传统的SPC手法就是有计画的在制程系统收集数据，以简单的管制图分析验证制程系统的变异是否有特殊原因存在或侦测是否有特殊原因存在。若有特殊原因存在，则须局部对策，发掘特殊原因，消除特殊原因，防止再发。并且持续监控制程系统，使制程系统保持稳定且可预测。

　　第四

　　当制程系统在统计的管制状态下时，也就是制程系统保持稳定且可预测。此时评估制程系统的制程能力，才真正能估计其符合规格的能力，亦可为制程系统持续改善的依据。品质管理发展至今，SPC的变异理论已经普遍在业界推广应用，只是很多人在用而不自知。譬如，ISO品质管理系统的建立、维护及稽核；品管圈活动步骤；福特汽车8D的改善程序；SIX SIGMA的活动程序。

　　规则一：一般可视为正确的管理方式，先对系统的变异进行解析，以分辨变异是来自特殊原因或共同原因。若有特殊原因，则进行局部对策，消除原因防止再发；若祇是系统的共同原因，则须由管理当局进行系统改善。

　　制程管制系统的目的是要经济有效地管制产品或制程品质。也就是说，当制程系统只有共同原因时，不要过度去调整或干预制程；当制程系统有特殊原因出现时，不要忽略局部对策的机会。制程管制系统的功能是要使制程系统在统计的管制状态下，使其变异只源自于系统的共同原因。以此来监控当特殊原因出现时能被察觉而给予局部对策，对产品或制程品质有不良影响的消除之，对产品或制程品质有益处的保留之。当制程系统在管制状态下时，即稳定且可预测，进行制程系统的改善，才有实质的效益。

　　规则二：一般可视为系统在共同原因的变异下，对系统缺乏认识的作业及管理人员对系统进行干预，而使系统产生结构性的变化。除非系统本身被一些可预测的因素影向，规则二可以应用来调整系统使之变异减少。例如，冷气机的自动调温系统，随着室温的改变来调整冷风的量，使得室温在设定的温度上。MacGregor 曾撰文解释在系统平均的变动可预测之下，规则二会较规则一的变异小。因此，解释规则二时必须假设系统在共同原因的变异下。下列几个实例说明之：

　　(1)自动化制程控制常以上一次制程测定的结果来调整制程；

　　(2)作业员以上一个工件的测定结果来调整补偿与目标值的差距；

　　(3)老师以学生考试的分数差目标值几分来决定处罚的轻重，使得程度差的学生自暴自弃；

　　(4)作菜时习惯先尝尝咸淡，再加水或加盐来中和咸淡，使得每次作的菜咸淡不一。

　　规则三：如规则二的补偿式调整，惟调整时回到目标值再调整其差值。在系统祗有共同原因时，其变异较规则二的调整方法更大而且上下交替大幅变动。下列几个实例说明之：

　　(1)自动化制程控制常以上一次制程测定的结果来调整制程，但以原设定补偿性调整；

　　(2)作业员以上一个工件的测定结果来调整与目标值的差距，但以原设定补偿性调整；

　　(3)业务员当月业绩低于目标10万元，下个月业绩必须达到目标再加10万。

　　(4)统独意识形态，依民意或选票，反向调整施政。

　　(5)赌博输钱或股票投资失利，加倍赌资或投资，希望把钱赢回来。

　　(6)公家机关本期预算没用完，下期多用一点补回来，不发白不发。

　　规则四：这是最常见的干预模式，几乎所有产业、政府及学术机构都可见到。下列几个实例可以说明之：

　　(1)作业员以上一次的生产结果为标准，依样画葫芦，而忘记原始的标准；

　　(2)工程变更时祗以上一版本为变更依据，而不追溯原始设计；

　　(3)教育训练时老鸟带新鸟或学长管学弟，造成训练的结果与原意愈差愈远；

　　(4)编制预算依上一期的结果乘上一个百分比为准，结果预算愈编愈大；

　　(5主持人给第一位表演者一个题目，表演给第二位表演者看，再由第二位表演给下一位看，依此类推，再由最后再一位表演者说出主持人给的题目是什么，通常是牛头不对马嘴。

　　(6)语言的演化，例如，台湾的闽南话或客家话与大陆、新马闽南语或客家话有所差异。

• 红珠实验