休哈特控制图

出自 MBA智库百科(https://wiki.mbalib.com/)

控制图(Control Chart)

　　休哈特控制图是由美国的贝尔电话实验所的休哈特(W.A.Shewhart)博士在1924年首先提出管制图使用后，管制图就一直成为科学管理的一个重要工具，特别在质量管理方面成了一个不可或缺的管理工具。它是一种有控制界限的图，用来区分引起质量波动的原因是偶然的还是系统的，可以提供系统原因存在的信息，从而判断生产过程是否处于受控状态。控制图按其用途可分为两类，一类是供分析用的控制图，用控制图分析生产过程中有关质量特性值的变化情况，看工序是否处于稳定受控状；再一类是供管理用的控制图，主要用于发现生产过程是否出现了异常情况，以预防产生不合格品。

　　控制图画在平面直角坐标系中，横坐标表示检测时间，纵坐标表示测得的目标特征值。按控制对象（目标特征值）的变化情况，控制图又分为两种：一种是稳值控制图，一种是变值控制图。

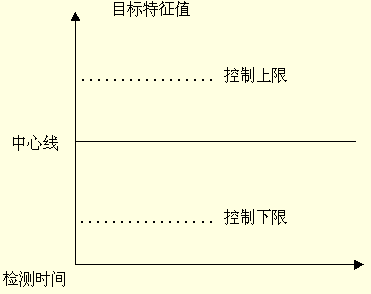
　　1、稳值控制图。稳值控制图一般用于对产品质量或目标值恒定不变的目标实施状态进行控制，如下图所示，图中中心线表示计划目标值，虚线表示控制上下限。

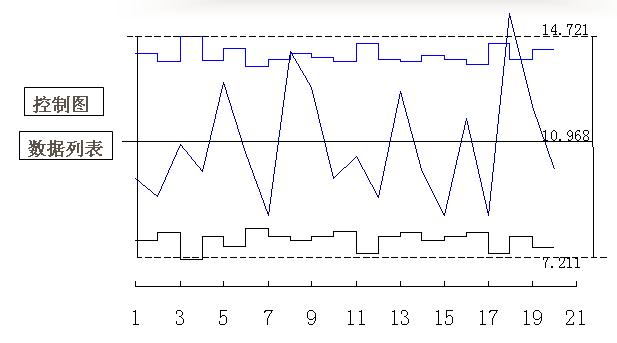
　　2、变值控制图。变值控制图用于对目标值随时间变化的目标实施状态进行控制。从计划线与实际线的对比，可看出目标实施状态，对于超出计划线的情况，查清超出的原因，采取措施，将其控制在计划线以下。

　　控制图是对过程质量加以测定、记录从而进行控制的一种科学方法。图上有中心线、上只存在偶然波动时，产品质量将形成某种典型分布。例如，在车制螺丝的例子中形成正态分布。如果除去偶然波动外还有异常波动，则产品质量的分布必将偏离原来的典型分布。因此，根据典型分布是否偏离就能判断异常因素是否发生，而典型分布的偏离可由控制图检出。在上述车制螺丝的例子中，由于发生了车刀磨损的异常因素，螺丝直径的分布偏离了原来的正态分布而向上移动，于是点子超出上控制界的概率大为增加，从而点子频频出界，表明在异常波动。控制图上的控制界限就是区分偶然波动与异常波动的科学界限，休哈特控制图的实质是区分偶然因素与异常因素两类因素。

　　1．控制图的预防原理

　　控制图是如何贯彻预防原则的呢？这可以由以下两点看出：

　　（1）应用控制图对生产过程不断监控，当异常因素刚一露出苗头，甚至在未造成不合格品之前就能及时被发现，在这种趋势造成不合格品之前就采取措施加以消除，起到预防的作用。

　　（2）在现场，更多的情况是控制图显示异常，表明异常原因已经发生，这时一定要贯彻“查出异因，采取措施，保证消除，不再出现，纳人标准。” 否则，控制图就形同虚设，不如不搞。每贯彻一次（即经过一次这样的循环）就消除一个异常因素，使它不再出现，从而起到预防的作用。

　　2．统计过程控制的实质

　　要精确地获得总体的具体数值，需要收集总体的每一个样品的数值。这对于一个无限总体或一个数量很大的有限总体来说往往是不可能的，或者是不必要的。在实际工作中，一般是从总体中随机地抽取样本，对总体参数进行统计推断。样本中含有总体的各种信息，因此样本是很宝贵的。但是如果不对样本进一步提炼、加工、整理，则总体的各种信息仍分散在样本的每个样品中。为了充分利用样本所含的各种信息，常常把样本加工成它的函数，一般将这个（或若干个）不含未知参数的样本函数称为统计量。

　　过程控制的实质，就是这样一个统计推断过程，所依据的统计量的形式应根据计推断的目的和应用的条件不同而有所不同。从实用和简化计算的角度来看，往往是利用样本的平均值和极差R来进行。

　　值得注意的是，利用样本的平均值及极差R推断总体的μ和σ时，由于总体构成的不均匀性以及抽样误差的存在，及R的变化同μ及σ的变化并不完全一样，即使在工序处于稳定状态下，μ及σ本身并无异常变化，但从工序中抽取样本的及R也是有所变化的也就是说，及R 都是随机变量，都有其特定的概率分布。它们各自的概率分布与总体分布既有一定的内在联系，又与总体分布不完全相同。在过程控制中，虽然通常依据一次抽样的结果进行一次统计推断，但由此所得出的结论却是建立在大量观测结果所遵循的统计规律的基础上的，是依样本统计量的概率分布来描述总体概率分布过程的。

　　1．计量值控制图

　　常用的计量值控制图有：平均值与极差控制图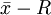（图）中位数与极差控制图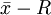（图）等等。其中尤以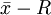图用得最多，它对加工工序有很强的控制能力，是控制产品质量最实用有效的一种工具

　　2．计数值控制图

　　常用计数值控制图由：不合格品数控值图；不合格品率控制图和单位缺陷控制图，缺陷控制图。

　　3．应用控制图需要考虑的问题

　　应用控制图需要考虑以下一些问题：

　　（1）控制图用于何处？原则上讲，对于任何过程，凡需要对质量进行控制管理的场合都可以应用控制图。但这里还要求：对于所确定的控制对象—— 质量指标应能够定量，这样才能应用计量值控制图。如果只有定性的描述而不能够定量，那就只能应用计数值控制图。所控制的过程必须具有重复性，即具有统计规律。对于只有一次性或少数几次的过程显然难于应用控制图进行控制。

　　（2）如何选择控制对象？在使用控制图时应选择能代表过程的主要质量指标作为控制对象。一个过程往往具有各种各样的特性，需要选择能够真正代表过程情况的指标。例如，假定某产品在强度方面有问题，就应该选择强度作为控制对象。在电动机装配车间，如果对于电动机轴的尺寸要求很高，这就需要把机轴直径作为我们的控制对象。

　　（3）怎样选择控制图？选择控制图主要考虑下列几点：首先根据所控制质量指标的数据性质来进行选择；其次，要确定过程中的异常因素是全部加以控制（全控）还是部分加以控制（选控），若为全控应采用休哈特图等；若为选控，应采用选控图。

　　（4）如何分析控制图？如果控制图中点子未出界，同时点子的排列也是随机的，则认为生产过程处于稳态或控制状态。如果控制图中点子出界（或不出界）而点子的排列是非随机的（也称为排列有缺陷），则认为生产过程失控。

　　（5）对于点子出界或违反其他准则的处理。若点子出界或点子的排列是非随机的，则应立即追查原因并采取措施防止它再出现。

　　（6）对于过程而言，控制图起着报警铃的作用，控制图点子出界就好比报警铃响，告诉现在是应该进行查找原因、采取措施、防止再犯的时刻了。一般来说，控制图只起报警铃的作用，而不能告诉这种报警究竟是由什么异常因素造成的。要找出造成异常的原因，除去根据生产和管理方面的技术与经验来解决外，应该强调指出，应用两种质量诊断理论和两种质量多元诊断理论来诊断的方法是十分重要的。

　　（7）控制图的重新制定。控制图是根据稳定状态下的条件5MIE来制定的。如果上述条件变化，如操作人员更换或通过学习操作水平显著提高，设备更新，采用新型原材料或其他原材料，改变工艺参数或采用新工艺，环境改变等，这时，控制图也必须重新加以制定。由于控制图是科学管理生产过程的重要依据，所以经过相当时间的使用后应重新抽取数据，进行计算，加以检验。 　　

　　一、计量值控制图

　　（一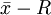）．控制图

　　对于计量数据而言，这是常用最基本的控制图。它的控制对象为长度、重量、纯度、时间和生产量等计量值的场合。但此图只适用于n<10的情况。

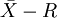　　 控制图的分析

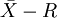　　控制图（以及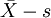控制图）是计量值最常用、最重要的控制图。

　　1. 适用范围广

　　图：若X服从正态分布，则易证也服从正态分布；若X非正态分布，则根据中心极限定理,可证近似服从正态分布。关键是这后一点才使图得以广为应用。

　　R图：通过在计算机上的模拟试验证实：只要X不是非常不对称的，则R的分布无大的变化，故也适用范围广。

　　2. 灵敏度高

　　图：对于偶波，会使标准偏差减少，从而使控制线UCL和LCL的间隔缩小。对于异波，由于一般异波所产生的变异往往是同一个方向的，故求平均值的操作对其无影响，因此，当异常时，描点出界就更加容易了，也即灵敏度高。

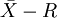　　控制图中，应该先作哪一个？

　　图与R图控制线的公式：

　　图：

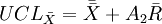
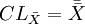
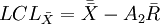
　　R图：

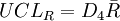
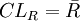
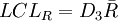
（1）若先 作图，则由于R 图还未判稳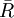，的数据不可用，故不可行。

（2）若先作R图，则由于R图中只有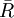一个数据，所以可行。等R图判稳后，再作图。

　　（3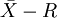）控制图的操作步骤如下：

　　步骤1：确定所控制的质量指标

　　①选择技术上最重要的控制对象

　　②指标之间有因果关系，取作为因的指标为统计量

　　③控制对象要明确，并为大家理解与同意

　　④控制对象要能以数字来表示

　　⑤控制对象要容易测定并对过程容易采取措施

　　⑥直接选择控制对象困难时采用代用特性进行测定

　　⑦同时控制多个对象，应用多元控制图与多元诊断

　　步骤2：取预备数据

　　① 样本组数至少取25组，最好再加上5组成为30组，以便必要时可去掉一些异常数据；

　　② 样本量（或样本大小）通常取为4或5；

　　③ 合理子组原则。

　　步骤3：计算。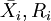

　　步骤4：计算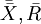

　　步骤5：计算R图控制线、图控制线，并作图。

　　步骤6：将预备数据在R图中打点，判稳。若稳，则进行步骤7；若不稳，则执行“20字方针”后转入步骤2，重新开始。

　　步骤7：将预备数据在图中打点，判稳。若稳，则进行步骤8；若不稳，则执行“20字方针”后转入步骤2，重新开始。

　　步骤8：计算过程能力指数并检验其是否满足技术要求，若过程能力指数满足技术要求，由转入步骤9。

　　步骤9：延长X-R控制图的控制线，作控制用控制图，进行日常管理。

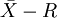　　图示例

　　【例-1】某手表厂为了提高手表的质量，应用排列图分析造成手表不合格品的各种原因，发现“停摆”占第一位。为了解决停摆问题，再次应用排列图分析造成停摆的原因，结果发现主要是由于螺栓脱落造成的。而后者则由螺栓松动造成。为此，厂方决定应用控制图对装配作业中的螺栓扭矩进行过程控制。

　　解：按照下列步骤建立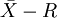图：

　　步骤1：取预备数据，将数据合理分成25组。

　　步骤2：计算各组样本的平均数。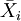

　　步骤3：计算各组样本的极差R_i。

　　步骤4：计算样本总均值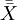与平均样本极差。

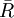　　步骤5：计算R图与图的参数，对状态判断。

　　步骤6：与规范进行比较，计算过程能力。

　　步骤7：延长上述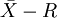图的控制线，对工序进行日常控制。

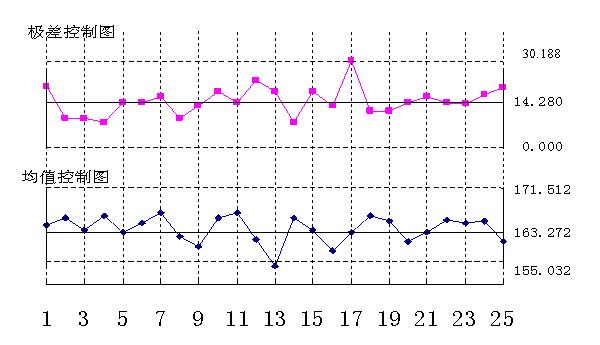
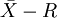　　控制图示例的第一次图

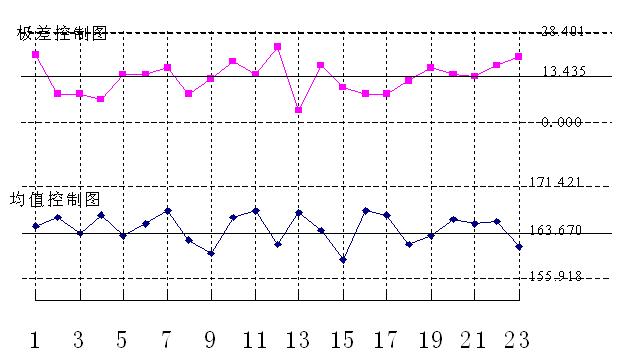
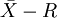　　控制图示例的第二次图

　　(二)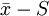．控制图

　　用标准差s控制总体参数σ的变化，当样本大小n>10或12，这时应用极差估计总体标准差的效率降低，需要用S图来代替R图。

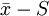　　控制图示例

　　【例-2】对【例-1】选用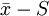图

　　步骤1：依据合理分组原则，取得25组预备数据；

　　步骤2：计算每个子组的平均值和标准差；

　　步骤3：计算所有观测值的总平均值和平均标准差；

　　步骤4：计算s图的控制限，绘制控制图；

　　步骤5：与容差限比较，计算过程能力指数；

　　步骤6：延长统计控制状态下的控制限，进入控制用控制图阶段，实现对过程的日常控制。

　　（三）．M_e − R控制图

　　用中位数图代替均值图。由于中位数的计算觉得，所以多用于现场需要把测定的数据直接记人控制图进行控制的场合，这时为了简便，当然规定奇数个数据。它受异常数据的影响较少。

　　Me－R图示例

　　【例-3】某机器生产点子盘片。规定的厚度为0.007-0.016cm。每隔半小时抽取样本量为5的样本（子组），记录其中心厚度（cm），如下表所示。拟建立一个中位数图以达到控制质量的目的。

云母盘片厚度的控制数据　　单位：0.001

子组号i	厚度					中位数Me	极差Ri
	X1	X2	X3	X4	X5
1	14	8	12	12	8	12	6
2	11	10	13	8	10	10	5
3	11	12	16	14	9	12	7
4	16	12	17	15	13	15	5
5	15	12	14	10	7	12	8
6	13	8	15	15	8	13	7
7	14	12	13	10	16	13	6
8	11	10	8	16	10	10	8
9	14	10	12	9	7	10	7
10	12	10	12	14	10	12	4
11	10	12	8	10	12	10	4
12	10	10	8	8	10	10	2
13	8	12	10	8	10	10	4
14	13	8	11	14	12	12	6
15	7	8	14	13	11	11	7

　　（四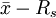）．，控制图

　　为了能够迅速反映现场情况，往往用X图代替图。

　　多用于下列场合：对每一个产品都进行检验，采用自动化检查和测量的场合；取样费时、昂贵的场合以及如化工等过程，样品均匀，多抽样也无太大的意义的场合。由于它不像前三种那样能取得较多的信息，所以它判断过程变化的灵敏都也要差一些。

　　X − R_s图示例

　　【例-4】下表给出了连续10批脱脂奶粉的样本“水分含量百分比”的实验室分析结果。将一个样本的奶粉作为一批的代表，在实验室对其成分特性进行分析测试，如脂肪、水分、酸度、溶解指数、沉积物、细菌及乳清蛋白。希望该过程的产品水分含量控制在4％一下。由于发现单批内的抽样变差可以忽略，因此决定每批只抽取一个观测值，并以连续各批的移动极差作为设置控制限的基础。

　　连续10个脱脂奶粉样本的水分含量百分比

　　（X：%水分含量；R：移动极差）

批号	1	2	3	4	5	6	7	8	9	10
X	2.9	3.2	3.6	4.3	3.8	3.5	3.0	3.1	3.6	3.5
R		0.3	.04	0.7	0.5	0.3	0.5	0.1	0.5	0.1

　　二、计数值控制图

　　1．p控制图

　　用于控制对象为不合格品率或合格率等计数值质量指标的场合。常见的不良率有不合格品率、废品率、交货延迟率、缺勤率、差错率等等。

　　当样本量大小n变化时，则p图的控制界限UCL_p与LCL_p将随样本大小n的变化呈现出凹凸状，不便于判稳或判异。

　　图-1 上下控制界线均呈现凹凸状的p图

　　2．np控制图

　　用于控制对象为不合格品数的场合。由于计算不合格品率需要进行除法，比较麻烦，所以样本大小相同的情况下，用此图比较方便。但当样本大小n变化时，np控制图的三条控制线都呈凹凸状，不但作图难，而且无法判稳、判异。故只有在样本大小相同的情况下，才应用此图。

　　3．c控制图

　　用于控制一部机器，一个部件一定的长度，一定的面积或任一定的单位中所出现的缺陷数目。但当样本量n发生变化时，c图上、中、下控制线将呈凹凸状，不便于判稳或判异。

　　4．U控制图

　　当样品的大小保持不变时可用C控制图，而当样品的大小变化时则应换算为平均每单位的缺陷数后再使用U控制图。但当n发生变化时，u图的二条控制线将呈凹凸状，给作图、判异、判稳造成困难。

　　控制图判断异常的准则有两条：点子出界就判断异常；界内点排列不随机判断异常。

　　1．判断稳态的准则

　　稳态是生产过程追求的目标。那么如何用控制图判断过程是否处于稳态？为此，需要制定判断稳态的准则。

　　判稳准则：在点子随机排列的情况下，符合下列各点之一就认为过程处于稳态：

　　（1）连续25个点子都在控制界限内；

　　（2）连续35个点子至多1个点子落在控制界限外；

　　（3）连续100个点子至多2个点子落在控制界限外。

　　2．判断异常的准则

　　在讨论控制图原理时，已经知道点子出界就判断异常，这是判断异常的最基本的一条准则。为了增加控制图使用者的信心，即使对于在控制界限内的点子也要观察其排列是否随机。若界内点排列非随机，则判断异常。

　　判断异常的准则：符合下列各点之一就认为过程存在异常因素：

　　（1）点子在控制界限外或恰在控制界限上控制界限内的点子排列；

　　（2）链：连续链，连续7个点以上排列在一侧；间断链，大多数点在一侧

　　（3）多数点靠近控制界限（在2-3倍的标准差区域内出现）

　　（4）倾向性与周期性。

　　1.不适应性的现象

　　现代制造模式具有复杂性、非线性、时变性、连续性、不确定性和不完全性等特点。它们使得休哈特控制图难以适应的具体表现为：质量数据采集量不足；有些工序数据不是正态分布；有些工序数据是大量的、海量的，如在线质量控制，由于计算机按时序在线采集数据，会致使工序质量数据量是大量的、海量的；质量控制要面对多过程和多参数；由于计算机集成制造和智能制造环境下的质量参数具有连续性、再现性等特点，致使质量数据相互相关；有的工序质量达到或接近零不合格过程，如时序参数长时间几乎不发生变化或微小变化，致使休哈特控制图在应用中失去判异作用，等等；形成了休哈特控制图不适应性的新环境。

　　2.应用条件和原理上的局限性

　　休哈特控制图是基于数理统计的原理，对生产过程中产生的系统原因进行识别并加以控制，从而达到对产品在生产过程中的质量控制，其应用条件主要有3个：

　　（1）质量特征数据是大批量的(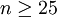,一般)；。

　　（2）质量特征数据是呈正态分布，或者接近正态分布；

　　（3）质量特征变量相互独立。即是判断随机变量X的数学问题；

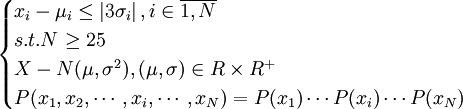
　　实际情况只要与3个应用条件之一发生冲突,就会发生休哈特控制图应用条件的限制。而休哈特控制图本身还存在精度不够的问题，以及休哈特控制图对数据量微小变化的迟钝等，属于休哈特控制图原理上的局限性。

　　3.造成不适应性的原因和解决方案

　　造成休哈特控制图的各种不适应性，其本质原因是应用条件的限制和原理上的局限性，前者导致了无法建立休哈特控制图，后者仅仅运用休哈特控制图已经达不到质量控制的目的；而客观原因是采集数据与大批量制造模式相比发生了变化。解决不适应性问题的出路有两个：一是化解本质原因，即改变休哈特控制图的局限性，将原休哈特控制图改造成为柔性动态的系统，由于以往休哈特控制图的斐然成绩，人们不习惯此改变；二是改变客观原因，即调整或改造质量数据的变化，经过变换之后能够适应休哈特控制图的应用条件，这是可行的解决方法。同时，质量数据不仅是休哈特控制图和其它质量控制方法的必要条件，还蕴涵着不同制造模式的特点。为此，需要分析各种制造模式与质量数据的关系，整理出规律，便于正确运用休哈特控制图，达到质量控制的目的。

• QC旧七大手法：控制图(SPC)、直方图、散布图、因果图、柏拉图、检查表、层别法。
• QC新七大手法：关系图法、KJ法、系统图法、矩阵图法、矩阵数据分析法、PDPC法、箭形图解法。