頻數分佈

出自 MBA智库百科(https://wiki.mbalib.com/)

頻數分佈（Frequency Distribution）

　　頻數也稱“次數”，對總數據按某種標準進行分組，統計出各個組內含個體的個數。我們把各個類別及其相應的頻數全部列出來就是“頻數分佈”或稱“次數分佈”。

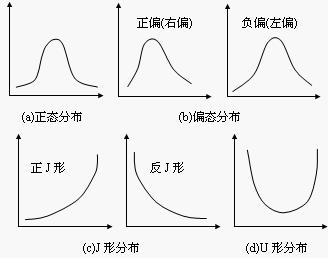
　　在日常生活和經濟管理中，常見的頻數分佈曲線主要有正態分佈（對稱分佈）、偏態分佈（skewed distribution）、J形分佈、U形分佈等幾種類型，如下圖所示：

　　正態分佈是一種對稱的鐘形分佈，有很多現象服從這種分佈，如農作物的單位面積產量、零件的公差、纖維強度等都服從正態分佈，如圖（a）。J形分佈有正J形和反J形兩種，如經濟學中供給曲線，隨著價格的提高供給量以更快的速度增加，呈現為正J形；而需求曲線則表現為隨著價格的提高需求量以較快的速度減少，呈現為反J形。U形分佈的特征是兩端的頻數分佈多，中間的頻數分佈少，比如，人和動物的死亡率分佈就近似服從U形分佈，因為人口中嬰幼兒和老年人的死亡率較高，而中青年的死亡率則較低；產品的故障率也有類似的分佈。

　　頻數分佈的兩個特征：集中趨勢（central tendency）和離散趨勢（tendency of dispersion）。

　　1、集中趨勢

　　大部分觀察值向某一數值集中的趨勢稱為集中趨勢，常用平均數指標來表示，各觀察值之間大小參差不齊。

　　2、離散趨勢

　　頻數由中央位置向兩側逐漸減少，稱離散趨勢，是個體差異所致，可用一系列的變異指標來反映。

　　①將原始資料按其數值大小重新排列

　　只有把得到的原始資料按其數值大小重新排列順序，才能看出變數分佈的集中趨勢和特點，為確定全距、組距和組數作准備。

　　②確定全距

　　全距是變數值中最大值和最小值的差數。確定全距，主要是確定變數值的變動範圍和變動幅度。如果是變動幅度不大的離散變數，即可編製單項式變數數列，如果是變數幅度較大的離散變數或者是連續變數，就要編製組距式變數數列。

　　③確定組距和組數

　　前面已經介紹過組距數列有等距和不等距之分，應視研究對象的特點和研究目的而定。

　　組距的大小和組數的多少，是互為條件和互相制約的。當全距一定時，組距大，組數就少；組距小，組數就多。在實際應用中，組距應是整數，最好是５或１０的整倍數。在確定組距時，必須考慮原始資料的分佈狀況和集中程度，註意組距的同質性，尤其是對帶有根本性的質量界限，絕不能混淆，否則就失去分組的意義。

　　在等距分組條件下，存在以下關係：

　　組數=全距/組距

　　④確定組限

　　組限要根據變數的性質來確定。如果變數值相對集中，無特大或特小的極端數值時，則採用閉口式，使最小組和最大組也都有下限和上限；反之，如果變數值相對比較分散，則採用開口式，使最小組只有上限（用“××以下”表示），最大組只有下限（用“××以上”表示）。如果是離散型變數，可根據具體情況採用不重疊組限或重疊組限的表示方法，而連續型變數則只能用重疊組限來表示。

　　在採用閉口式時，應做到最小組的下限低於最小變數值，最大組的上限高於最大變數值，但不要過於懸殊。

　　⑤編製變數數列

　　經過統計分組，明確了全距、組距、組數和組限及組限表示方法以後，就可以把變數值歸類排列，最後把各組單位數經綜合後填入相應的各組次數欄中。