標誌變動度

出自 MBA智库百科(https://wiki.mbalib.com/)

　　標誌變動度是綜合反映總體各單位標誌值變異程度的指標。簡稱變異指標。它顯示總體中變數數值分佈的離散趨勢，是說明總體特征的另一個重要指標，與平均數的作用相輔相成。

　　標誌變動度可用來反映平均數代表現象一般水平的代表性程度，標誌變動度愈小，則平均數的代表性愈大。它可以說明現象的穩定性和均衡性。它和平均指標結合應用還可以比較不同總體標誌值的相對差異程度。常用標誌變動度指標有全距、四分位差、平均差、標準差等。

　　全距 　

　　全距也稱極差，是最簡單的變異指標。總體各單位標誌值中最大值和最小值的差距V。它最簡明地說明標誌值的變動範圍。

　　V。=Xmax − Xmin

　　四分位差　

　　總體數量標誌值數列中各四分位數離差的平均數。將數列分成四等分，中間形成三個分割點，居於第一分割點的標誌值Q1稱為第一四分位數，居於第二分割點的標誌值Q2即中位數，稱為第二四分位數，居於第三分割點的標誌值Q3稱為第三四分位數。四分位差的算式為： 　　

　　四分位差==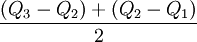

　　四分位差能夠避免次數分配數列中兩端極端數值的影響，中間部分數列分配愈集中，標誌值的差異愈小，四分位差也愈小。

　　平均差　

　　總體各單位標誌值與平均數離差絕對值的平均數。它表示總體各標誌值與平均數的平均差異程度。求平均差所以用離差的絕對值，是因為任何數列各標誌值與算術平均數的正負離差之和都等於0，而取絕對值可以不考慮離差的正負號，只考慮離差數大小。以A D表示平均差，其算式為：

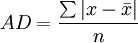
　　式中x代表標誌值，塣代表平均數，n代表總體單位數。

　　平均差受總體各單位所有標誌值的影響，所以更能綜合反映總體標誌的變異程度，平均差愈小表示標誌變異愈小，分佈愈集中。

　　不同總體的平均差計量不同，單位不同，不能直接對比。為了顯示平均離差的相對程度，便於不同總體的比較，可以計算平均差繫數VAD，它是將平均差除以平均數求得。其計算公式為：

　　標準差　

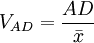
　　總體各單位標誌值與平均數離差平方的平均數的平方根，又稱均方差。它反映標誌值與平均數離差的平均水平，是測定標誌變動度最常用的指標。求標準差所以將離差加以平方，是因為可以消除離差的正負號，並將離差程度強化，最後把所得結果開方是為了恢複原來的計量單位。以σ 表示標準差，其計算公式如下： 　　

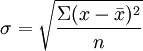
　　 為便於不同總體的對比，可以計算標準差繫數V_σ，以測定標誌值的相對變異程度。其計算公式是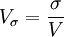：。