标志变动度

出自 MBA智库百科(https://wiki.mbalib.com/)

　　标志变动度是综合反映总体各单位标志值变异程度的指标。简称变异指标。它显示总体中变量数值分布的离散趋势，是说明总体特征的另一个重要指标，与平均数的作用相辅相成。

　　标志变动度可用来反映平均数代表现象一般水平的代表性程度，标志变动度愈小，则平均数的代表性愈大。它可以说明现象的稳定性和均衡性。它和平均指标结合应用还可以比较不同总体标志值的相对差异程度。常用标志变动度指标有全距、四分位差、平均差、标准差等。

　　全距 　

　　全距也称极差，是最简单的变异指标。总体各单位标志值中最大值和最小值的差距V。它最简明地说明标志值的变动范围。

　　V。=Xmax − Xmin

　　四分位差　

　　总体数量标志值数列中各四分位数离差的平均数。将数列分成四等分，中间形成三个分割点，居于第一分割点的标志值Q1称为第一四分位数，居于第二分割点的标志值Q2即中位数，称为第二四分位数，居于第三分割点的标志值Q3称为第三四分位数。四分位差的算式为： 　　

　　四分位差==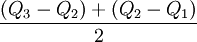

　　四分位差能够避免次数分配数列中两端极端数值的影响，中间部分数列分配愈集中，标志值的差异愈小，四分位差也愈小。

　　平均差　

　　总体各单位标志值与平均数离差绝对值的平均数。它表示总体各标志值与平均数的平均差异程度。求平均差所以用离差的绝对值，是因为任何数列各标志值与算术平均数的正负离差之和都等于0，而取绝对值可以不考虑离差的正负号，只考虑离差数大小。以A D表示平均差，其算式为：

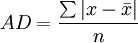
　　式中x代表标志值，塣代表平均数，n代表总体单位数。

　　平均差受总体各单位所有标志值的影响，所以更能综合反映总体标志的变异程度，平均差愈小表示标志变异愈小，分布愈集中。

　　不同总体的平均差计量不同，单位不同，不能直接对比。为了显示平均离差的相对程度，便于不同总体的比较，可以计算平均差系数VAD，它是将平均差除以平均数求得。其计算公式为：

　　标准差　

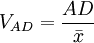
　　总体各单位标志值与平均数离差平方的平均数的平方根，又称均方差。它反映标志值与平均数离差的平均水平，是测定标志变动度最常用的指标。求标准差所以将离差加以平方，是因为可以消除离差的正负号，并将离差程度强化，最后把所得结果开方是为了恢复原来的计量单位。以σ 表示标准差，其计算公式如下： 　　

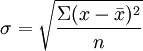
　　 为便于不同总体的对比，可以计算标准差系数V_σ，以测定标志值的相对变异程度。其计算公式是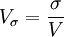：。