四分位差
出自 MBA智库百科(https://wiki.mbalib.com/)
四分位差(Quartile Deviation)
目录 |
什么是四分位差[1]
四分位差又称内距、也称四分间距(inter-quartile range),是指将各个变量值按大小顺序排列,然后将此数列分成四等份,所得第三个四分位上的值与第一个四分位上的值的差。
四分位差的公式[1]
四分位差用公式表示:
Q = Q3 − Q1
其中:Q1的位置=(n+1)/4
Q3的位置=3(n+1)/4
四分位差若图所示:
四分位差的特点[2]
四分位差反映了中间50%数据的离散程度。其数值越小,说明中间的数据越集中;数值越大,说明中间的数据越分散。与极差(最大值与最小值之差)相比,四分位差不受极值的影响。此外,由于中位数处于数据的中间位置,因此四分位差的大小在一定程度上也说明了中位数对一组数据的代表程度。
四分位差的适用范围[2]
四分位差主要用于测度顺序数据的离散程度。当然,对于数值型数据也可以计算四分位差,但不适合于分类数据。
四分位差的计算方法[3]
如果所给的数据资料不同,四分位差的具体计算方法也不同:
- 1.未分组数据
首先对数据进行排序,求出Ql、Q3所在的位置;其次根据位置确定其对应的标志值即Ql、Q3;最后计算二者差额的一半,即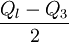 就是四分位差。
就是四分位差。
Ql的位置=
Q3的位置=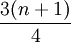
- 2.单项式数列
先计算各组的累计次数,然后确定分位点位置。
Ql的位置=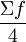
Q3的位置=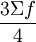
对于上面的两种情况,若(n+1)或Σf恰好为4的倍数,则计算出来的四分位数的位置就是整数,这时,各个位置上的变量值就是相应的四分位数;若(n+1)或Σf不是4的倍数,则按上面公式计算出来的四分位数的位次就可能带有小数,这时可根据插值法来计算上下四分位数。再按公式计算出四分位差。
假设样本容量为50时, =12.75,
=12.75,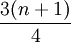 =38.25,则按插值法可得:
=38.25,则按插值法可得:
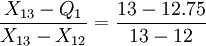
整理得:Q1=0.25X12+0.75X13
同样可得:Q3=0.75X38+0.25X39
- 3.组距式数列
先计算上、下四分位的值,然后再计算四分位差。此时计算四分位数的基本原理与中位数相类似。计算公式如下:
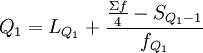 ×
×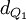
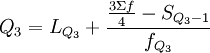 ×
×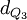
式中,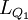 ,
,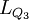 ,分别代表下四分位和上四分位数所在组的下限;
,分别代表下四分位和上四分位数所在组的下限;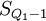 ,
,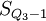 分别代表下四分位和上四分位数所在组以下的累计次数;
分别代表下四分位和上四分位数所在组以下的累计次数;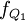 ,
,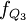 分别代表下四分位和上四分位数所在组的次数。
分别代表下四分位和上四分位数所在组的次数。
四分位差的计算案例[4]
例1:由7人组成的旅游小团队年龄分别为:17、19、22、24、25、28、34,求其年龄的四分位差。计算步骤为:
①计算Q1,与Q3的位置。
Q1的位置=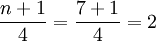
Q3的位置=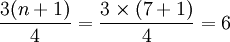
即Q1与Q3的位置分别为第2位和第6位。
②确定Q1与Q3的数值。
Q1=19(岁)
Q3=28(岁)
即第2位和第6位对应年龄分别为19岁和28岁。
③计算四分位差。
Q.D.=Q3 − Q1=28-19=9(岁)
④含义。说明该旅游小团队有50%的人年龄集中在19~28岁之间,最大差异为9岁。
例2:由8人组成的旅游小团队年龄分别为:17、19、22、24、25、28、34、38,求其年龄的四分位差。计算步骤为:
①计算Q1与Q3的位置。
Q1的位置=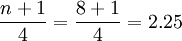
Q3的位置=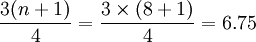
即Q1与Q3的位置分别为第2.25位和第6.75位。
②确定Q1与Q3的数值。由于Q1与Q3的位置带有小数,所以Q1与Q3的数值要按照小数点后数值的比例在相临的两个数值之间进行分摊。即:
Ql=0.75x2+0.25x3=0.75×19+0.25×22=19.75(岁)
Q3=O.25x6+O.75x7=0.25×28+0.75×34=32.5(岁)
③计算四分位差。
Q.D.=Q3-Q1=32.5—19.75=12.75(岁)
④含义。说明该旅游小团队有50%的人年龄集中在19.75岁至32.5岁之间,最大差异为12.75岁。
(2)分组资料计算的四分位差。
例3:根据某车间工人日产量分组资料,如表1所示,计算四分位差。
| 按日产量分组(个) | 工人数f(人) | 向上累计工人数F(人) |
| 5~10 | 12 | 12 |
| 10~15 | 46 | 58 |
| 15~20 | 36 | 94 |
| 20~25 | 6 | 100 |
| 合计 | 100 | —— |
计算步骤为:
①确定Q1与Q3的位置。
Q1的位置=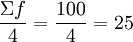
根据向上累计工人数可知Q1在第2组即10~15内。
Q3的位置=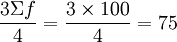
根据向上累计工人数可知,Q3在第3组即15~20内。
②计算Q1与Q3的数值。
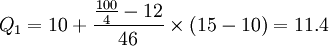 (个)
(个)
 (个)
(个)
③计算四分位差。
Q.D.=Q3-Ql=17.4-11.4=6(个)
④含义。计算结果表明,有50%(一半)工人的日产量分布在11.4~17.4之间,且最大差异为6个。
四分位差的优点表现为不受两端各25%数值的影响,能对开口组数列的差异程度进行测度,可以衡量中位数代表性高低。缺点为不能反映所有标志值的差异程度。








公式上写Q1的位置是n+1/4,Q3的位置是3(n+1)/4。为什么举例里面就都不加1了呢? 不懂。