失效率

出自 MBA智库百科(https://wiki.mbalib.com/)

失效率（Failure rate）

　　所謂失效率是指工作到某一時刻尚未失效的產品，在該時刻後，單位時間內發生失效的概率。一般記為λ,它也是時間t的函數,故也記為λ(t),稱為失效率函數,有時也稱為故障率函數或風險函數。在極值理論中，失效率稱為“強度函數”；在經濟學中，稱它的倒數為“密爾（Mill）率”；在人壽保險事故中，稱它為“死亡率強度”。

　　按上述定義,失效率是在時刻t尚未失效產品在t + Δt的單位時間內發生失效的條件概率.即

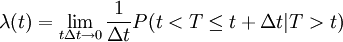
　　它反映t時刻失效的速率,也稱為瞬時失效率。

　　為了理解失效率函數的概念，現對它作一個更直觀的剖析。設在t=0時有N個產品投試，到時刻t已有n(t)個產品失效，尚有N-n(t)個產品在工作。再過Δt時間，即到t + Δt時刻，有Δn(t) = n(t + Δt) − n(t)個產品失效。那麼，產品在時刻t前未失效而在時間(t,t + Δt)內失效率為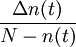。而在時刻t前未失效、在時刻t後的單位時間內發生失效的頻率亦即失效率的估計值。

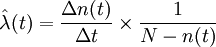　　現在來倒出失效率的數學表達式。按定義, 失效率是在時刻t尚未失效產品在t + Δt的單位時間內發生失效的條件概率，即

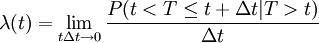
　　由條件概率公式的性質和時間的包含關係，可知

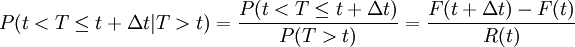
　　於是:

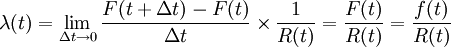
　　這就是失效率的數學表達式。

　　失效率的觀測值是在某時刻後單位時間內失效的產品數與工作到該時刻尚未失效的產品數之比。

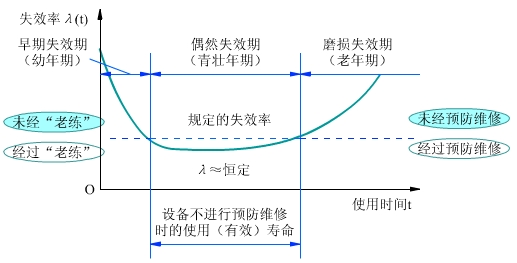
　　如果我們以失效率(單位時間內發生失效的比率)來描述產品失效的發展過程，那麼，在不進行預防性維修的情況下，設備、元件的失效率λ與其工作(使用)時間t之間具有如圖1所示的典型失效率曲線。因為這種曲線的形狀與浴盆相似，故稱為“浴盆曲線”。

　　　　　　　　圖1-典型失效率曲線-浴盆曲線

　　按照“失效率曲線”的形狀，即按照產品失效的發展過程，可以將整個失效過程分為三個時期：

　　(1)早期失效期(遞減型)。在產品的使用初期，容易暴露由於設計和製造上的缺陷而導致失效，因此產品的早期失效率很高。隨著使用時間的延長，失效率則很快下降。產品的早期失效期相當於人的“幼年期”。如果在產品出廠之前，進行旨在剔除這類缺陷的“老練”過程，即進行可靠性實驗，那麼在產品以後的使用時，從一開始便可使失效率大體保持恆定值。

　　(2)偶然失效期(恆定型)。在理想的情況下，產品在發生磨損或老化以前，應是無“失效”的，但是由於環境的偶然變化、操作時的人為偶然差錯或者由於管理不善造成的“潛在缺陷”，仍有產品的偶然失效。產品的偶然失效率是隨機分佈的、很低的和基本上是恆定的，故又稱為隨機的失效期。偶然失效期相當人的“青壯年期”，這一時期是產品的最佳工作時期。偶然失效率的倒數即為無失效的平均時間。

　　(3)磨損失效期(遞增型)。經過偶然失效期後，設備中的元件已到了壽命終止期，於是失效率開始極劇增加，這標誌產品已進入“老年期”，這時的失效叫做磨損失效，又稱為耗損失效。如果在進入磨損失效期之前，進行必要的預防維修，它的失效率仍可保持在偶然失效率附近，從而延長產品的偶然失效期。

　　產品失效按其發展過程分類對可靠性工程來說是十分有用的。