偏態分佈
出自 MBA智库百科(https://wiki.mbalib.com/)
偏態分佈(Skewed distribution)
目錄 |
頻數分佈有正態分佈和偏態分佈之分。正態分佈是指多數頻數集中在中央位置,兩端的頻數分佈大致對稱。
偏態分佈是指頻數分佈不對稱,集中位置偏向一側。若集中位置偏向數值小的一側,稱為正偏態分佈;集中位置偏向數值大的一側,稱為負偏態分佈。
偏態分佈只有滿足一定的條件(如樣本例數夠大等)才可以看做近似正態分佈。
與正態分佈相對而言,偏態分佈有兩個特點:
一是左右不對稱(即所謂偏態);
二是當樣本增大時,其均數趨向正態分佈。
一個偏態分佈的集中趨勢[1]
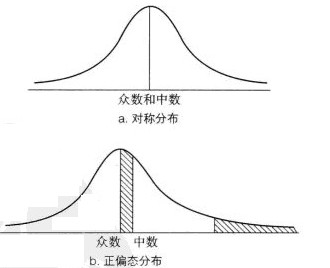
當一個單峰分佈呈很強的偏態形狀時,你很難決定是否用中數還是均數代表分佈的集中趨勢(在這種情況下,眾數也絕不可能是三者中最好的一個)。另一方面,對於圖2a所示的對稱單峰分佈,均數和中數都十分精確地位於中央,眾數也正位於此。因為分佈是對稱的,所以眾數的兩側面積也相等。現在讓我們來看看當加入幾個高分數使得分佈變成正偏態分佈,情況會變成怎樣(如圖2b所示)。在右側加入少量分數會使得右側面積略微增加。為了使得兩側面積相等,中數必須往右移一點點。但是,請註意,中數並不需要沿著X軸移動太多。因為中數位於分佈中比較厚的部分,所以只需往右稍移一點便足以彌補足夠的面積給新加入的高分數(請看圖2b中右端陰影部分是如何與中數和眾數之間的陰影區域相等的)。可見,中數並不受到分佈偏態的強烈影響,從而在描述分佈的集中趨勢方面很有優勢。
圖2 一個偏態分佈的中數
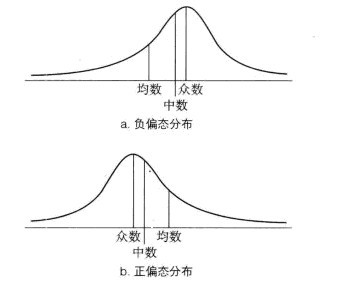
事實上,一旦你求出了一個分佈的中數,則你可以取分佈中任何一側的一個分數,並將其移動遠離中數。只要這個分數還是位於中數的其中一邊,則你可以任意移動它到你想要的任何遠的位置,中數都不會改變它原有的位置。但對於均數則不是這樣了。均數會受到分佈中任何一個分數的影響。因此,均數會被拉到偏態尾巴的方向,有時會被拉動很多,如圖2所示。當分佈呈負偏態時(圖3a),均數會移至中數的左側(即變得更負了),而對於正偏態的情況(圖3b)則恰恰相反。反之,如果你同時有一個分佈的均數和中數,而中數更高(即更正),那麼該分佈是負偏態;如果均數更高,那麼該分佈是正偏態。在一個正偏態分佈中,超過一半的分數低於均數,而負偏態的情況則想反。如果均數和中數是相等的,則分佈很可能是圍繞中心對稱的。
圖3 一個偏態分佈的均數
- ↑ (美)BARRY H. COHEN著;高定國等譯.心理統計學.華東師範大學出版社









左偏分佈圖有點問題,不容易看出來