銷售人員意見調查法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是銷售人員意見調查法[1]
銷售人員意見調查法是指銷售預測的進行是在集合有關銷售人員的個人意見的基礎上,而作出的測算和判斷。
由於銷售員最接近市場上的顧客和用戶,他們比較熟悉和瞭解消費者以及競爭對手的情況,尤其是對·自己的“轄區”市場,往往比其它人員瞭解得更為清楚。因此,所作出的銷售預測具有很大的參考價值。在一般情況下,銷售人員為數眾多,綜合他們的意見所作的預測具有較高的現實性。企業派出的銷售人員在各地市場上推銷產品,他們非常瞭解當地的經濟發展情況,當有的推銷入員看到當地農業的生產情況,就知道農民的收入會受到什麼因素的影響,對那些產品(如農機、化肥、農藥等)需求量的狀況。當企業收集了全部銷售人員的估測數據後,進行彙總綜合計算,從而求出未來時期的銷售預測值。
銷售人員意見調查法的優點[1]
銷售員意見綜合法的優點是:
1.利用銷售員對市場熟悉的特點以及具有的專業知識,所得到的預測數據比較準確。
2.銷售員參加市場預測,其本身會增加他們完成任務的信心。
銷售人員意見調查法的缺點[1]
這種預測方法的缺點是:
1.預測者負有單純完成目標的任務觀點,難免採取穩健態度,導致預測值易於偏低。
2.銷售人員用於預測的時間過多,就會影響推銷業務的開展。
3.容易忽視對總體市場(即整個市場系統)的經濟成長髮展趨勢進行客觀的分析,而產生過於樂觀或過於悲觀的估計。
銷售人員意見調查法預測方法與步驟[1]
預測方法與步驟:
第一步,首先要求每個銷售員作出自己的銷售預測,負責銷售的經理可給予有關未來巨集觀經濟環境變動的資料。例如:政府的預測,有關經濟與商業展望的資料。銷售員利用這些資料加上自己的判斷,可作一個自己認為“最佳”的預測數字。現設三個銷售員在某市場投放的某種商品的最佳銷售預測數字如表所列:
| 銷售員 | 銷售預測(單位) |
| 甲 | 30 |
| 乙 | 40 |
| 丙 | 20 |
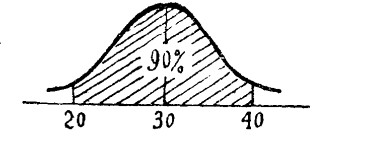
第二步,銷售員甲認為下一期該商品的預測銷售量在20與40單位之間的可能性為90%,即表示銷售在20與40單位之間出現的概率為90%。在常態分配曲線上(即正東分佈曲線),該銷售員的最佳預測數值為30單位。事實上即為期望值(expected vallte)或平均銷售值。如下圖所示。
平均銷售為30單位時與最高銷售40單位和最低銷售20單位之差為10單位,根據以1為標準差的標準分數(standard score,Z)即概率度的模式來看:
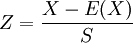
式中:
X——為大於或小於期望值的隨機變數(即最高銷售40單位或最低銷住20單位);
E(X)——期望值或平均餡;
S——樣本標準差。
數理統計證明:隨著概率度Z不斷增大,概率P(Z)的數位就越趨近於1,即接近於完全可倍程度。概率表中P(Z)獲示與概率度Z相應的概率,它們之間呈函數關係。有了概率度Z,即可查出概率P=P(Z);反過來也可以在一定的概率保證下(即預定的準確程度)查出概率度Z。當概率為0.9時,可查概率表找出其對應的Z=1.65:
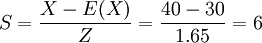
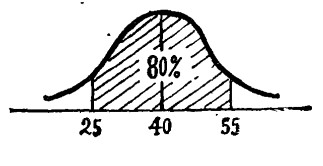
同理,銷售員乙的平均銷售期望值為40單位,在銷售25與55單位之間出現的概率為0.8(如下圖所示)其對應的Z=1.28。則:
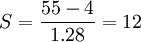
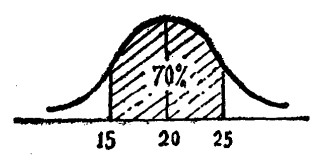
銷售員丙的平均銷售期望值為20單位,在15與25單位之間的概率為0.7(如下圖所示),其對應的Z=1.04。則:
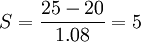
第三步,計算三個銷售員的總期望值。如下表所列:
| 銷售員 | 期望值 | 標準差S | 變異數S2 |
| 甲 | 30 | 6 | 36 |
| 乙 | 40 | 12 | 144 |
| 丙 | 20 | 5 | 25 |
總計 | 90 | - | 205 |
總期望值90單位的標準差St為:
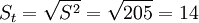 (單位)
(單位)
第四步,預測下期的銷售值。
有了總期望值和標準差,就可以預測下一時期的鍋賜位。它是一個以E(X)為均值,以S為標準的正態分佈曲線,這條曲線與橫軸所夾的面積為100%。因此,總銷售值的可信區段,在可信水平為68.27%時,即期望值落在可信區段中的可靠性的程度,其相對應的Z=1時,總銷售期塑值的可信區段為:
90-(1)U<E(X)<90+(1)14
76<E(X)<104
如果將可信水平提高到95.45%時,WZ=2,則總銷售期望值的可信區段為;
90—(2)N<E(X)<90十(2)N
62<E(X)<118
如果將可信水平提高到99.73%時,即Z=3,則總銷售期望值的可信區段為;
90-(3)14<E(X)<90+(3)14
48<E(X)<132
可信水平與可信區段之間呈反向的關係。可信水平愈高,則可信區段愈寬;反之,則愈窄。如果取98.73%的可信水平,則可信區段當然很寬,但是過寬的區段估計會導致誤差過大,則會失去市場預測的意義。如果採取68.27%的可信水平,則可信區段估計較窄,對產品銷售決策的意義較大,但是該區段估計出現的可能性較低。通常市場預測可取不高也不低的中等可信水平為95.45%,當遇到市場變化較大時,應由決策者根據實際情況,來加以選擇。