销售人员意见调查法
出自 MBA智库百科(https://wiki.mbalib.com/)
目录 |
什么是销售人员意见调查法[1]
销售人员意见调查法是指销售预测的进行是在集合有关销售人员的个人意见的基础上,而作出的测算和判断。
由于销售员最接近市场上的顾客和用户,他们比较熟悉和了解消费者以及竞争对手的情况,尤其是对·自己的“辖区”市场,往往比其它人员了解得更为清楚。因此,所作出的销售预测具有很大的参考价值。在一般情况下,销售人员为数众多,综合他们的意见所作的预测具有较高的现实性。企业派出的销售人员在各地市场上推销产品,他们非常了解当地的经济发展情况,当有的推销入员看到当地农业的生产情况,就知道农民的收入会受到什么因素的影响,对那些产品(如农机、化肥、农药等)需求量的状况。当企业收集了全部销售人员的估测数据后,进行汇总综合计算,从而求出未来时期的销售预测值。
销售人员意见调查法的优点[1]
销售员意见综合法的优点是:
1.利用销售员对市场熟悉的特点以及具有的专业知识,所得到的预测数据比较准确。
2.销售员参加市场预测,其本身会增加他们完成任务的信心。
销售人员意见调查法的缺点[1]
这种预测方法的缺点是:
1.预测者负有单纯完成目标的任务观点,难免采取稳健态度,导致预测值易于偏低。
2.销售人员用于预测的时间过多,就会影响推销业务的开展。
3.容易忽视对总体市场(即整个市场系统)的经济成长发展趋势进行客观的分析,而产生过于乐观或过于悲观的估计。
销售人员意见调查法预测方法与步骤[1]
预测方法与步骤:
第一步,首先要求每个销售员作出自己的销售预测,负责销售的经理可给予有关未来宏观经济环境变动的资料。例如:政府的预测,有关经济与商业展望的资料。销售员利用这些资料加上自己的判断,可作一个自己认为“最佳”的预测数字。现设三个销售员在某市场投放的某种商品的最佳销售预测数字如表所列:
| 销售员 | 销售预测(单位) |
| 甲 | 30 |
| 乙 | 40 |
| 丙 | 20 |
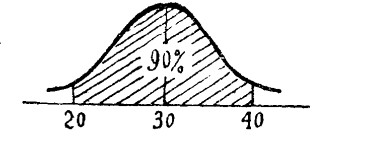
第二步,销售员甲认为下一期该商品的预测销售量在20与40单位之间的可能性为90%,即表示销售在20与40单位之间出现的概率为90%。在常态分配曲线上(即正东分布曲线),该销售员的最佳预测数值为30单位。事实上即为期望值(expected vallte)或平均销售值。如下图所示。
平均销售为30单位时与最高销售40单位和最低销售20单位之差为10单位,根据以1为标准差的标准分数(standard score,Z)即概率度的模式来看:
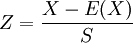
式中:
X——为大于或小于期望值的随机变量(即最高销售40单位或最低销住20单位);
E(X)——期望值或平均馅;
S——样本标准差。
数理统计证明:随着概率度Z不断增大,概率P(Z)的数位就越趋近于1,即接近于完全可倍程度。概率表中P(Z)获示与概率度Z相应的概率,它们之间呈函数关系。有了概率度Z,即可查出概率P=P(Z);反过来也可以在一定的概率保证下(即预定的准确程度)查出概率度Z。当概率为0.9时,可查概率表找出其对应的Z=1.65:
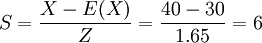
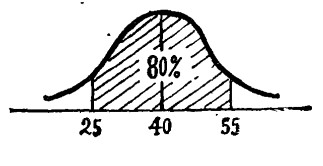
同理,销售员乙的平均销售期望值为40单位,在销售25与55单位之间出现的概率为0.8(如下图所示)其对应的Z=1.28。则:
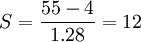
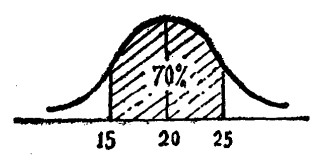
销售员丙的平均销售期望值为20单位,在15与25单位之间的概率为0.7(如下图所示),其对应的Z=1.04。则:
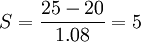
第三步,计算三个销售员的总期望值。如下表所列:
| 销售员 | 期望值 | 标准差S | 变异数S2 |
| 甲 | 30 | 6 | 36 |
| 乙 | 40 | 12 | 144 |
| 丙 | 20 | 5 | 25 |
总计 | 90 | - | 205 |
总期望值90单位的标准差St为:
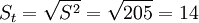 (单位)
(单位)
第四步,预测下期的销售值。
有了总期望值和标准差,就可以预测下一时期的锅赐位。它是一个以E(X)为均值,以S为标准的正态分布曲线,这条曲线与横轴所夹的面积为100%。因此,总销售值的可信区段,在可信水平为68.27%时,即期望值落在可信区段中的可靠性的程度,其相对应的Z=1时,总销售期塑值的可信区段为:
90-(1)U<E(X)<90+(1)14
76<E(X)<104
如果将可信水平提高到95.45%时,WZ=2,则总销售期望值的可信区段为;
90—(2)N<E(X)<90十(2)N
62<E(X)<118
如果将可信水平提高到99.73%时,即Z=3,则总销售期望值的可信区段为;
90-(3)14<E(X)<90+(3)14
48<E(X)<132
可信水平与可信区段之间呈反向的关系。可信水平愈高,则可信区段愈宽;反之,则愈窄。如果取98.73%的可信水平,则可信区段当然很宽,但是过宽的区段估计会导致误差过大,则会失去市场预测的意义。如果采取68.27%的可信水平,则可信区段估计较窄,对产品销售决策的意义较大,但是该区段估计出现的可能性较低。通常市场预测可取不高也不低的中等可信水平为95.45%,当遇到市场变化较大时,应由决策者根据实际情况,来加以选择。