配對交易

出自 MBA智库百科(https://wiki.mbalib.com/)

　　配對交易是指八十年代中期華爾街著名投行Morgan Stanley的數量交易員Nunzio Tartaglia成立的一個數量分析團隊提出的一種市場中性投資策略，，其成員主要是物理學家、數學家、以及電腦學家。

　　Ganapathy Vidyamurthy在《Pairs Trading: Quantitative Methods and Analysis》一書中定義配對交易為兩種類型：一類是基於統計套利的配對交易，一類是基於風險套利的配對交易。

　　基於統計套利的配對交易策略是一種市場中性策略，具體的說，是指從市場上找出歷史股價走勢相近的股票進行配對，當配對的股票價格差（Spreads）偏離歷史均值時，則做空股價較高的股票同時買進股價較低的股票，等待他們回歸到長期均衡關係，由此賺取兩股票價格收斂的報酬。

　　配對交易策略的基本原理是基於兩個相關性較高的股票或者其他證券，如果在未來時期保持著良好的相關性，一旦兩者之間出現了背離的走勢，且這種背離在未來是會得到糾正的，那麼就可能產生套利的機會。對於配對交易的實踐而言，如果兩個相關性較高的股票或者其他證券之間出現背離，就應該買進表現相對較差的，賣出表現相對較好的。當未來兩者之間的背離得到糾正，那麼可以進行相反的平倉操作來獲取利潤。

　　由於配對交易利用配對間的短期錯誤定價，通過持有相對低估，賣空相對高估，因此其本質上是一個反轉投資策略，其核心是學術文獻中的股票價格均值回覆。儘管配對交易策略非常簡單，但卻被廣泛應用，其之所以能被廣泛應用的主要原因是:首先，配對交易的收益與市場相獨立，即市場中性，也就是說它與市場的上漲或者下跌無關;其次，其收益的波動性相對較小;第三，其收益相對穩定。

　　第一，配對交易利用了兩個資產的短暫價格偏離的對稱性，進行對沖以獲取兩個資產的Alpha收益，其核心假設是配對資產的價差具有均值回覆性。而這種均值回覆是以交易者的非理性行為相關的。因為當市場中存在大量這類想法的交易者時，股票價格會產生上升的慣性，但這種上升慣性僅僅由於這一個非理性因素所驅動，並沒有具體實際的基本面因素支撐，因而股價很快會跌落。相反，股價下跌的股票也會產生下跌的慣性，當市場的理性因素占據主導時，價格又回覆到原先的水平。而如果交易者能夠採用配對交易策略，就可以獲得這兩項資產價格偏離的收益了。在實際操作中，其執行過程可以簡單地描述為：投資者首先選擇相互匹配的兩個資產，當配對資產價格差異增加的時候，做多價格偏低的資產，同時做空價格偏高的資產，而當價格差異減小的時候，則結束頭寸，完成交易；同時，為了控制風險，當價差進一步擴大時，需要在適當的止損點結束頭寸。

　　第二，配對交易是一種市場中性的交易策略。當觀察到配對的資產價格差異增大到一定程度時，對價格上升的資產建立空頭，對價格下跌的資產建立多頭。在一價定律的作用下，配對資產的價格差異將很快減小。這時，再買入價格下跌的資產對沖之前建立的空頭頭寸，同時賣出價格上漲的資產，獲取兩項資產的收益。就整個過程來看，配對交易在單一資產上都有系統風險和個別風險，但由於頭寸始終是相反的，因此系統風險完全對沖，配對交易整體上只承擔了配對資產的個別風險。而在一價定律下，價格對於價值的回覆使得配對的資產的個別風險直接轉換為個別收益。這種收益是於市場無關的。

　　Vidvamurthy(2004)通過利用資產之間的協整關係，嘗試對配對交易使用參數化交易規則。Vidvamurthv採用Engle and Granger(1987)的協整兩步法，設資產A,B價格序列為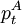,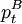，則對數股票價格間的長期均衡關係可以表示為:

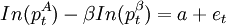
　　式中，a是常數項，e_t是零均值的平穩時間序列，標準化的協整向量為(1, − β)，協整誤差e_t視為錯誤定價，它反映了基於協整關係的股票組合偏離均衡關係的情況。

　　使用協整方法建立的股票多空組合，從長期來看組合中的股票之間具有均衡穩定關係。當股票價格變動使得該組合出現對長期關係的偏離，基於協整理論，可以預期這樣的偏離或者波動是暫時的，在長期內會由於一支或兩支股票的調整而回覆到均衡關係。長期來看，股票市場中錯誤定價關係能夠被修正，並不能給投資者帶來收益。但是，這種偏差在中、短期股票市場中是存在的，並且反映出一定的趨勢持續和反轉的特性。Vidvamurthy(2004)認為可以在市場中捕捉這樣的偏差，設置合適的策略來獲得收益。Vidvamurthv(2004)通過協整回歸估計得到的殘差序列:錯誤定價序列{Et}是平穩的，圍繞其均值來回震蕩，當超過某個臨界值時可認為是異常行為，從而建立合適的頭寸在回覆到均值時來獲取利潤。

　　隨機價差(Stochastic Spread)法是由Elliott et a1.,(2005)提出的，對資產價差序列利用狀態空間模型進行建模。Elliottet a1.,(2005)將資產A, B價格序列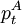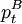，的差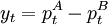的均值回覆行為在連續時間情形下建模，採

　　用狀態空間方法，令價格差由一潛在狀態變數x_t驅動，x_t遵循vasicek過程:

　　dx_t = k(θ − x_t)dt + σdB_t

　　上式中，dB_t為標準布朗運動。其中狀態變數x_t，以速度K返回其均值θ，將可觀測的價差表示為一均值回覆過程和高斯雜訊和，即:y_t = x_t + w_t

　　兩個就構成了一個狀態空間模型，該模型有以下三個主要優點:

　　首先，抓住了配對交易的核心，即均值回覆性。嚴格地說價差應該表示為對數價格差即: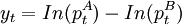。一般說來，兩隻股票的價格差的長期均值不是常數，而會隨著兩者價格上升變大，下降而變小;而採用對數價差可以避免出現上述問題。

　　其次，該模型是一個連續模型，因此可以用於預測。交易者可計算價差返回到其長期均值的時間，從而對配對交易關鍵的問題—如期望持有時間和期望收益，可以很容易計算。

　　最後，該模型易處理，參數可通過卡爾曼濾波方法估計。參數估計量是極大似然估計量且在最小均方誤差下最優。對參數估計，採用歐拉離散化從而有狀態方程

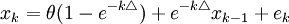
　　式中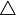，表示兩次觀測之間的時間間隔(以年為單位)，觀測方程為:

　　y_k = x_k + w_k

　　有了上述的方程，可利用卡爾曼濾波遞歸程式可對參數ψ = θ,k,σ做出最優估計。

　　Gatev et a1.,(2006)等運用最小距離法在標準化價格空間找出股票的相應配對，設置合適的交易規則併進行實證檢驗，發現配對交易可獲取利潤。最小距離法是一種非參數化方法，計算股票價格序列間的歐氏距離或者標準化的股票價格序列間的平方距離和來度量價差，進而衡量股票之間相對

　　錯誤定價程度。選擇合適的形成期，通過使標準化的股票價格序列間的平方距離最小化來選取相應的配對。配對選擇後進人交易期，當兩者之間標準化序列的差超過某個臨界值則產生交易。