協整理論

出自 MBA智库百科(https://wiki.mbalib.com/)

　　協整是指若兩個或多個非平穩的變數序列，其某個線性組合後的序列呈平穩性。

　　協整理論的作用在於正確地解釋了經濟現象和預測現象，誤差修正模型（ECM）將影響變化的因素有效地分解成長期靜態關係和短期動態關係之和。其中格蘭傑定理證明瞭協整關係與誤差修正模型之間的關係，指出若幹個一階非平穩經濟變數間若存在協整關係，那麼這些變數一定存在誤差修正模型表達式，反之也成立。

　　1、20世紀70年代以前的建模技術以時間序列平穩為前提設計的。

　　2、理論假定與現實的矛盾。

　　3、協整理論的產生---計量經濟學方法研究的新階段

　　---Granger首先提出了偽回歸問題（1974）；

　　----1978年，Engle—Granger發表論文“協整與誤差修正”，正式提出“協整”（cointegration）概念

　　協整理論是Engleand Granger在1978年首先提出來的。在此之前，人們為了避免出現謬誤回歸，往往只採用平穩時間序列來建立回歸模型，或者先將非平穩時間序列轉化為平穩時間序列，然後再作回歸。有了協整理論，幾個同階單整的時間序列之間可能存在一種長期的穩定關係，其線性組合可能降低單整階數。在經濟領域中，許多情況下通過經濟理論我們可以知道某兩個變數應該是協整的，利用協整理論，我們可以給出一個確切地判斷，通過協整檢驗就是對經濟理論正確性的檢驗。近些年來，協整理論在我國經濟領域的應用有了快速的發展。例如在巨集觀經濟研究中，朱運法，張彥群（1998）討論了中國季度巨集觀經濟計量的協整模型。在居民消費與GDP之間的關係研究中，朱江，田映華和孫全（2003）從協整理論出發，對我國居民消費與GDP建立了誤差修正模型。在能源消費研究中，馬超群、儲慧斌、李科和周四清（2004）採用協整理論分析中國從1954～2003年間能源消費和經濟增長的年度數據，分析了GDP與能源消費的各組成部分(包括煤、石油、天然氣和水電等)之間的協整關係，並且建立了具有誤差修正項的長期均衡方程，對模型結果也進行了分析。在金融貨幣的運行研究中，關山燕，甄紅線（2001）運用協整理論，給出了我國的貨幣需求的誤差修正模型。

　　所謂的協整是指若兩個或多個非平穩的變數序列，其某個線性組合後的序列呈平穩性。此時我們稱這些變數序列間有協整關係存在。為了給出協整關係的精確定義，我們需要先給出單整的概念，如果一個時間序列{y_t}在成為穩定序列之前必須經過d次差分，則稱該時間序列是d階單整。記為y_t~I(d)。下麵我們可以給出協整關係的精確定義，設隨機向量X_t中所含分量均為d階單整，記為X_t~I(d)。如果存在一個非零向量β，使得隨機向量Y_t=βX_t~I(d-b),b>0，則稱隨機向量X_t具有d，b階協整關係，記為X_t~CI(d,b)，向量β被稱為協整向量。特別地，y_t和x_t為隨機變數，並且y_t,x_t~I(1)，當y_t = k₀ + k₁x_t~I(0)，則稱y_t和x_t是協整的，(k₀,k₁)稱為協整繫數。

　　關於協整的概念，我們給以下說明：首先，協整回歸的所有變數必須是同階單整的，協整關係的這個前提並非意味著所有同階單整的變數都是協整的，比如假定y_t,x_t~I(1)，y_t和x_t的線性組合仍為I(1)，則此時y_t和x_t雖然滿足同階單整，但不是協整的。其次，在兩變數的協整方程中，協整向量(k₀,k₁)是唯一的，然而，若系統中含有k個變數，則可能有k-1個協整關係。協整檢驗和估計協整線性系統參數的統計理論構成了協整理論的重要組成部分。如果沒有它們，那麼協整在實踐中便會失去其應有的重要作用。常用的協整檢驗有兩種，即Engle-Granger兩步協整檢驗法和Johansen協整檢驗法。這兩種方法的主要差別在於Engle-Granger兩步協整檢驗法兩步法採用的是一元方程技術，而Johansen協整檢驗法採用的是多元方程技術。因此Johansen協整檢驗法在假設和應用上所受的限制較少。

　　1、Engle-Granger兩步協整檢驗法

　　Engle-Granger兩步協整檢驗法考慮瞭如何檢驗零假設為一組I(1)變數的無協整關係問題。他們用普通最小二乘法估計這些變數之間的平穩關係繫數，然後用單位根檢驗來檢驗殘差。拒絕存在單位根的零假設是協整關係存在的證據。我們從最簡單的情況開始討論，設兩個變數y_t和x_t都是序列，考慮下列長期靜態回歸模型

　　y_t = β₀ + β₁x_t + ε_t (1)

　　對於上述的模型的參數，我們用最小二乘法給出其參數估計。利用MacKinnon給出的協整ADF檢驗統計量，檢驗在上述估計下得到的回歸方程的殘差ε_t是否平穩（如果y_t和x_t不是協整的，則他們的任意組合都是非平穩的，因此殘差ε_t將是非平穩的）。也就是說，我們檢驗殘差ε_t的非平穩的假設，就是檢驗y_t和x_t不是協整的假設。更一般地，我們有以下具體方法：

　　(1)使用ADF檢驗長期靜態模型中所有變數的單整階數。協整回歸要求所有的解釋變數都是一階單整的，因此，高階單整變數需要進行差分，以獲得I(1)序列。

　　(2)用OLS法估計長期靜態回歸方程，然後用ADF統計量檢驗殘差估計值的平穩性。

　　2、Johansen協整檢驗法

　　當長期靜態模型中有兩個以上變數時，協整關係就可能不止一種。此時若採用Engle-Granger協整檢驗，就無法找到兩個以上的協整向量。Johansen和Juselius提出了一種在VAR系統下用極大似然估計來檢驗多變數之間協整關係的方法，通常稱為Johansen協整檢驗。具體做法是如下：

　　設一個VAR模型如下

　　Y_t = B₁Y_{t − 1} + B₂Y_{t − 2} + ... + B_pY_{t − p} + U_t (2)

　　其中Y_t為m維隨機向量，B_i(i=1,2,...,p)是m×m階參數矩陣，U_t~IID(0,σ)。我們將(2)式轉換為

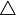　　Y_t=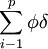Y_{t − i}+φY_{t − p}+U_t (3)

　　(3)式稱為向量誤差修正模型(VECM)，即一次差分的VAR模型加上誤差修正項φY_{t − p}，設置誤差修正項的主要目的是將系統中因差分而喪失的長期信息引導回來。在這裡φ_t=-(I-B_1-...-B_i)，φ=-(I-B_1-...-B_p)。參數矩陣φ_i和φ分別是對Y_t變化的短期和長期調整，m×m階矩陣φ的秩記為r，則存在三種情況：

　　(i)r=m，即φ是滿秩的，表示Y_t向量中各變數皆為平穩序列；

　　(ii)r=0，φ表示為空矩陣，Y_t向量中各變數無協整關係；

　　(iii)0<r≤m-1，在這種情況下，φ陣可以分解為兩個m×r階(滿列秩)矩陣α和β的積，即φ = αβ'。其中α表示對非均衡調整的速度，β為長期繫數矩陣(或稱協整向量矩陣)，即β'的每一行β_i'是一個協整向量，秩r是系統中協整向量的個數。儘管α和β本身不是唯一的，但β唯一地定義一個協整空間。因此，可以對α和β進行適當的正規化。

　　這樣，協整向量的個數可以通過考察φ的特征根的顯著性求得。若矩陣φ的秩為r，說明矩陣φ有r個非零特征根，按大小排列為λ₁,λ₂,...,λ₃。特征根的個數可通過下麵兩個統計量來計算：

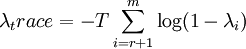　　 (4)

　　λ_max = − Tlog(1 − λr + 1) (5)

　　其中λ_i是式(3)中φ矩陣特征根的估計值，T為樣本容量。

　　(4)式稱為跡檢驗，

　　H₀:r<m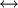H₁:r=m

　　(5)式稱為最大特征根檢驗，

　　H₀:r=q,q=1,2,...,m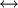H₁:r≤q+1

　　原假設隱含著λ_{r + 1}=λ_{r + 2}=...=λ_m=0，表示此系統中存在m-r個單位根，最初先設原假設有m個單位根，即r=0，若拒絕原假設H₀，表示λ₁>0，有一個協整關係；再繼續檢驗有(m-1)個單位根，若拒絕原假設H₀，表示有兩個協整關係；依次檢驗直至無法拒絕H₀為止。Johansen與Juselius在蒙特卡羅模擬方法的基礎上，給出了兩個統計量的臨界值，目前大多數計量經濟軟體都直接報告出檢驗結果。關於這一節的具體計算，藉助於統計分析軟體包，我們可以很方便地得到計算結果，這裡略去。

　　研究變數之間的協整關係，對研究經濟問題的定量分析有著重要的意義：

　　（1）定量描述經濟規律：協整表明儘管兩個序列雖然都是非平穩的I(1)，但兩者的某個線性組合卻可能存在一種平穩關係。這種平穩關係，對於研究經濟學中變數之間存在的穩定的經濟規律的定量描述具有很重要的意義。研究變數之間的協整關係，就等於研究變數之間的定量規律。

　　（2）避免偽回歸。如果一組非平穩時間序列不存在協整關係，則根據它們構造的回歸模型就可能是偽回歸。偽回歸模型儘管有很高的R²值和t值，但OLS的參數估計值卻是非一致的（這種結果看上去很好但卻是毫無意義的回歸，被格蘭傑（Granger）和紐博爾德（Newbold）稱為偽回歸）。

　　一般在時間序列的回歸中，DW值很低而R²卻很高，就應懷疑存在偽回歸的可能。如果建立模型前，對變數之間的協整關係進行了檢驗，證明瞭它們是協整的，那麼所建立的回歸模型則可以避免偽回歸。所以，對變數之間的協整檢驗是避免偽回歸的事先預防。

　　（3）區分變數之間的長期均衡關係和短期波動關係。長期均衡關係就是指兩個時間序列共同漂移的方式。短期波動關係是指y_t對長期趨勢的偏離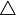y_t與x_t對長期趨勢的偏離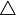x_t之間的關係。誤差修正模型便是一種能同時考慮變數之間這兩種關係的一種模型。