協整檢驗
出自 MBA智库百科(https://wiki.mbalib.com/)
協整檢驗(Cointegration Test)
目錄 |
非平穩序列很可能出現偽回歸,協整的意義就是檢驗它們的回歸方程所描述的因果關係是否是偽回歸,即檢驗變數之間是否存在穩定的關係。所以,非平穩序列的因果關係檢驗就是協整檢驗。
在目前巨集觀經濟計量分析中,Granger(1987)所提出的協整方法已成為了分析非平穩經濟變數之間數量關係的最主要工具之一,且通過線性誤差修正模型(ECM)刻畫了經濟變數之間的線性調整機制,這就是所謂的線性協整方法。近年來,隨著經濟理論的發展,尤其是交易成本和政策反應的經濟分析中,傳統的線性協整分析已不再是合適的分析方法,鑒於此Balk和Fomby(1997)提出了所謂的閾值協整(Threshold Cointegraion)方法,它刻畫了經濟變數之間的非線性調整機制。如在股票交易過程中,由於交易費用、交易政策等因素會導致股價的非對稱調整;國家的貨幣政策由於制度方面的原因也會對通貨膨脹率產生非對稱調整行為。因此閾值協整方法論是分析這類經濟問題的最有力的工具之一。閾值協整是對Granger(1987)提出的用來描述經濟變數Xt=(X1t,X2t,……Xkt)和Yt之間長期關係的協整概念的至關重要發展。眾所周知,協整是指如果經濟變數之間存在長期協整關係,且正則化協整向量是(1,-β′),則Xt、Yβ之間的長期均衡關係可以表示為:
Yβ=β′Xt+μt (1)
其中Xt、Yt都是I(1)過程,μt是I(O)過程,且可以表示為一個平穩的自回歸過程。而當Balke和Fomby(1997)把閾值協整引入巨集觀經濟分析時,他們認為如果(1)式中的協整誤差項μt的數據生成過程(DGP)是以下閾值自回歸:
其中:β參數是變數之間的協整繫數向量,γ是閾值變數,d是轉換變數,d是滯後參數,則這種協整稱之為閾值協整。如果協整誤差項是形如式(2)的數據生成機制,則稱為Two-Regime的閾值協整;如果是形如式(3)的誤差生成機制,則稱為Three-Regime的閾值協整。在以前的研究中,對於式(2)和式(3)所表示的閾值協整,大多研究都集中在ρ、q、θ、λ四個參數都小於1的情形,而對其它情形研究較少(Enders和Granger(1998))。本文主要研究如下情形,即:
此時式(2)和式(3)所表示的閾值協整即所謂的部分協整(Partial Cointegration)。針對部分協整檢驗,caner和Hansen(2001)提出一個統計量,且Gouveia和Rodrigues(2004)將該統計量應用閾值協整檢驗,但是他們並沒有對該統計量的檢驗勢進行研究。而在我們以前的研究中發現:該統計量在檢驗閾值協整時具有低勢。因此,本文一方面提出一個新的統計量來檢驗部分協整,並通過模擬研究該統計量的檢驗水平和檢驗勢,同時也和Engle-Granger(1987)年所提出的EG兩步法(簡記為EG法)進行了比較;另一方面將部分協整擴展到Enders和Siklos(2001)提出的沖量部分協整(Momentum Partial Cointegration,即M-部分協整),並對其進行系統的模擬研究。
協整即存在共同的隨機性趨勢。協整檢驗的目的是決定一組非平穩序列的線性組合是否具有穩定的均衡關係,偽回歸的一種特殊情況即是兩個時間序列的趨勢成分相同,此時可能利用這種共同趨勢修正回歸使之可靠。正是由於協整傳遞出了一種長期均衡關係,若是能在看來具有單獨隨機性趨勢的幾個變數之間找到一種可靠聯繫,那麼通過引入這種醉漢與狗之間距離的“相對平穩”對模型進行調整,可以排除單位根帶來的隨機性趨勢,即所稱的誤差修正模型。
在進行時間系列分析時,傳統上要求所用的時間系列必須是平穩的,即沒有隨機趨勢或確定趨勢,否則會產生“偽回歸”問題。但是,在現實經濟中的時間系列通常是非平穩的,我們可以對它進行差分把它變平穩,但這樣會讓我們失去總量的長期信息,而這些信息對分析問題來說又是必要的,所以用協整來解決此問題。
統計量檢驗勢和檢驗水平、漸近P-值的模擬步驟
infT統計量由於包含有備擇假設中的贅餘參數,其漸近分佈是非標準的,即不再是標準的t分佈,那麼通過模擬來研究該統計量的性質成為了當前的主流辦法。所以對該統計量的檢驗勢和檢驗水平性質的研究,也通過電腦模擬來實現。為了簡單起見,通過雙變數模型來模擬研究檢驗統計量,具體的模擬步驟如下:
①生成部分協整的雙變數的I(1)數據,且協整誤差項是由(6)式所生成;
②確定潛在閾值的取值範圍,上、下界分別取轉換變數的15%、85%的分位數,並構造該區間作為閾γ值的潛在取值;
③構造式(7)所示的ECM模型,併在給定閾值γ的條件下計算φ的條件t值,然後在閾值γ的潛在取值範圍內搜索t(γ)的最小值infT的值;
⑤利用上文中的FRB法確定該統計量的漸近P-值或通過下文的模擬臨界值確定檢驗勢。
對於infT統計量檢驗水平的模擬研究,模擬步驟基本不變,只是在第一步的數據生成中,要生成不協整的雙變數的I(1)數據,然後根據:
Size=Prob(infT*>infT)
來確定檢驗水平。
由於infT統計量的極限分佈是非標準的t分佈,因此本文采用自助法來確定該統計量的漸近P-值與檢驗水平,同時也採用統計量的模擬臨界值研究檢驗勢和水平。自助法由Efron(1979)提出,在計量經濟學檢驗中應用十分廣泛,尤其在統計量的抽樣分佈無法得到的情況下,運用該方法研究檢驗統計量的檢驗勢和水平顯得尤為重要。同時在式(7)的ECM模型中,協整誤差項在原假設下是非平穩的,所以本文將採用Hansen[11](2000)提出的固定回歸元自助法(Fixed Regressor Bootstrap Method,簡記FRB)來確定統計量的漸近P值和檢驗水平。其基本步驟如下:首先讓式(7)的被解釋變數從獨立同分佈的標準正態中抽取,即~innd(0,1);如果是異方差時,通過獲得被解釋變數序列,其中是式(7)在原假設下的OLS估計殘差序列~innd(0,1)。第二步在式(7)的ECM模型中,固定回歸元(即固定解釋變數數據序列),並對模型進行OLS估計,計算統計量t(γ)。第三步在潛在閾值γ的取值區間內,搜索infT*值,由此通過下式獲得infT統計量的漸近P-值和檢驗水平:
asyP-value=Prob(infT<infT*)
Seo(2006)基於閾值向量誤差修正模型(TVECM)提出了原假設:沒有協整,備擇假設是閾值協整的檢驗方法,但是該方法不能把部分協整從閾值協整中區分出來,因此本文為了彌補這一缺陷,提出了新的檢驗統計量,來進一步檢驗閾值協整是否是部分協整。不失一般性式(2)可以寫成:
其中Γ是潛在的閾值區間,在本文中我們以轉換變數的15%分位數和85%分位數作為閾值的潛在範圍(Andrews,1993)。如果φ和的t值只有其中一個顯著,則此時的協整就是部分協整,如果兩個t值都顯著則認為是閾值協整(即在Two-Regime閾值協整中,兩個Regimes中都是平穩過程或在Three-Regime的閾值協整中,兩頭的Regimes都是平穩過程)。另外在式(1)中也可以加入截距項或趨勢項,檢驗步驟和沒有截距和趨勢項的檢驗是一樣的。
通過對檢驗統計量的模擬研究,研究表明在檢驗所謂的部分協整和M-部分協整時,固定回歸元自助法的統計量具有較高的檢驗勢,但是固定回歸元自助法在檢驗部分協整和M-部分協整時具有較嚴重的水平扭曲且都會增大“棄真”的概率,而利用模擬臨界值進行檢驗水平模擬時具有較小的水平扭曲;其次採取模擬臨界值的檢驗法會隨著數據序列“持久性”的增強,其檢驗勢呈下降趨勢,但下降速度沒有EG兩步法快;第三模擬臨界值的檢驗法在檢驗M-部分協整時比檢驗部分協整時具有較低的檢驗勢。
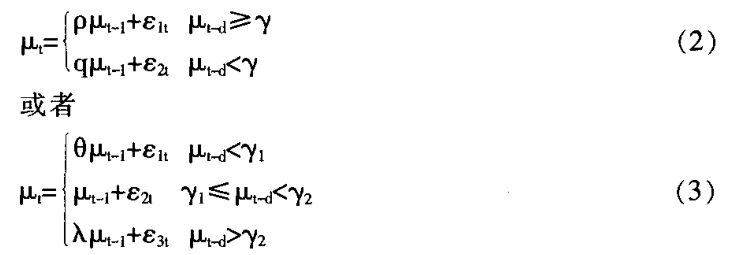
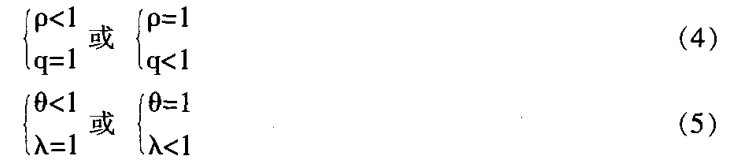








,則之間的長期均衡關係可以表示為…… 後邊的圖呢!圖呢!