卡爾曼濾波

出自 MBA智库百科(https://wiki.mbalib.com/)

卡爾曼濾波（Kalman Filtering）

　　最佳線性濾波理論起源於40年代美國科學家Wiener和前蘇聯科學家Ｋолмогоров等人的研究工作，後人統稱為維納濾波理論。從理論上說，維納濾波的最大缺點是必須用到無限過去的數據，不適用於實時處理。為了剋服這一缺點，60年代Kalman把狀態空間模型引入濾波理論，並導出了一套遞推估計演算法，後人稱之為卡爾曼濾波理論。卡爾曼濾波是以最小均方誤差為估計的最佳準則，來尋求一套遞推估計的演算法，其基本思想是：採用信號與雜訊的狀態空間模型，利用前一時刻地估計值和現時刻的觀測值來更新對狀態變數的估計，求出現時刻的估計值。它適合於實時處理和電腦運算。

　　卡爾曼濾波的實質是由量測值重構系統的狀態向量。它以“預測—實測—修正”的順序遞推，根據系統的量測值來消除隨機干擾，再現系統的狀態，或根據系統的量測值從被污染的系統中恢復系統的本來面目。

　　1、模型要求

　　卡爾曼濾波要求模型已知。即模型的結構與參數已知，且隨機向量的統計特征已知。

　　2、卡爾曼濾波分類

　　記Y_j的向量函數：

　　為狀態X（k)的估計量，分三種情況：

• 當k>j時，稱為預測；
• 當k=j時，稱為濾波；
• 當k<j時，稱為平滑。

　　卡爾曼濾波是解決狀態空間模型估計與預測的有力工具之一，它不需存儲歷史數據，且可以同過電腦程式到達對狀態空間模型的優化擬合。

　　一、基於卡爾曼濾波方法的時用水量預測

　　在20世紀60年代以後，數學家卡爾曼提出了用一個狀態方程和一個量測方程來完整描述線性動態過程，從而形成了一種遞推濾波演算法，卡爾曼濾波不要求保留使用過的觀測數據，當測得新的使用數據，可按照一套遞推公式算出新的估計量，不必重新計算，此外，他還打破了對平穩過程的限制，可用於對時變隨機信號的濾波，卡爾曼濾波是一套基本的公式，可用於預測修正的評估，在最小化協方差估計誤差方面表現出眾。

　　一個動態系統的狀態變化，在沒有外部干擾時，系統的未來狀態可以根據現時狀態從已知的運動方程中確定出來，但是，遺憾的是總是存在各種外部干擾，同時人們對運動方程的描述不可能十分精確，例如方程的建立過程中忽略影響小的量或者將非線性形式簡化為線性形式，變參數近似表示成常參數等等^[2]。當線性方程的描述在人們所需範圍內足夠準確時，可以認為該線性系統的行為看作兩部分組成。一部分是由已知的運動方程正確的預測出來，另一部分是可以看作均值為零的隨機分量^{[3] [4]}。

　　設每小時用水量為x(k)。對於不同時間值k，均有一值x(k)與之對應，當取樣時刻變化時，就得到一時用水量序列{x(k)}，用水量預測序列{x(k)}為白雜訊序列{x(k)}驅動的一階遞歸模型，狀態方程如下：

　　x(k) = φ(k)x(k − 1) + ω(k − 1)　　(1)

　　西(_|})為七一1時刻和居時刻時用水量之間的相關係數，本文中採用了時變模型，認為F是一個隨時間變化的繫數塒為表示過程雜訊。

　　測量方程如下：y(k)=Hx(k)+v(k)　　(2)

　　y(k)為k時刻用水量的量測值；

　　日為量測參數，它由測量系統和測量方法所確定。不隨時間變化的一個常量，取為1；v(k)為量測雜訊。

　　均方估計誤差為p(k) = E[x(k) − x(k)]²，在均方估計誤差為最小的準則下加以推導，可以得出一套遞推公式如下：

　　預測估計方程：

　　x(k + 1 | k) = F(k)x(k | k − 1) + b(k)[y(k) − Hx(k | k − 1)]　　(3)

　　預測增益方程：

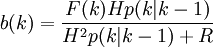　　　　(4)

　　均方預測誤差方程：

　　p(k | k + 1) = F(k)²p(k | k − 1) − F(k)Hb(k)p(k | k − 1) + Q

　　式中： x(k+1|k)於後時刻的k+1時刻時用水量基礎的估計值；R為量測雜訊的方差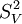，；Q為過程雜訊的方差，。

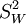　　卡爾曼濾波是以預測加修正來實現其濾波遞推的，卡爾曼濾波的這個性質使得我們很容易用電腦來實現，從而完成我們對時用水量的預測。

　　二、基於卡爾曼濾波方法的季節預測模型

　　為了提高預測精度，引進了2個參數的預測採用如下狀態方程和量測方程：

　　x(k) = φ₁(k)x(k − 1) + φ₂(k)x(k − 2) + ω(k)x(k − 1)

　　y(k)=Hx(k)+v(k)　　(6)

　　以矩陣的形式表示如下:。

　　　　(7)

　　在最小均方差準則^[5](即p(k|k+1)=E[x(k+1)-x(k+1|k)]^2為最小)下得如下遞推公式。

　　預測估計方程：

　　x(k+1|k)=Ax(k|k-1)+G(k)[(k)-CX(k|k-1)]　　(8)

　　預測增益方程:

　　G(k) = AP(k | k − 1)H^T[HP(k | k − 1)H^T + R(k)¹　　(9)

　　預測協方差方程

　　P(k+1|k)=[A-G(k)H]P(k|k-1)A^T+Q(k)　　(10)

　　其中A為[F(k)₁F(k)₂],X(K | k − 1)為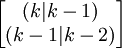,Y(k)為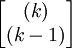

　　由於每天用水量呈現一定的周期 ,現以過去一天同一時刻的時用水量作為衝擊序列^[6],對 k 時刻時用水量做出修正，因此在 2個參數的基礎上加入季節模型。

　　狀態方程和量測方程如下:

　　x(k) = φ₁(k)x(k − 1) + φ₂(k)u(k) + w(k − 1)

　　y(k)=Hx(k)+v(k)

　　其中u(k)=x(k-24)

　　即將第2個參數x提前24h ,重新統計出由F₁和F₂構成的A矩陣 ,進行相應的卡爾曼濾波預測。重新構建的模型稱為卡爾曼濾波季節預測模型。

　　三、工程實例

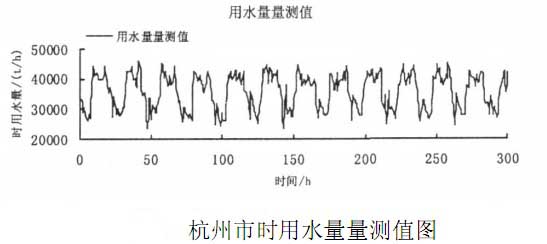
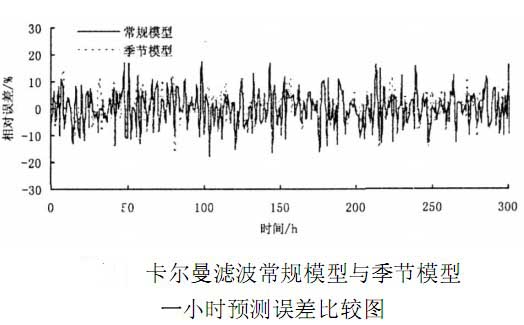
　　杭州位於錢塘江畔,是一個人口密集城市,其設計供水量能力為140萬t/d。本文以杭州市的時用水量為例,分別採用卡爾曼濾波模型以及卡爾曼濾波季節模型進行預測,對結果進行比較分析(見二圖),研究上述2種方法的利弊。

　　從圖中可以看出,對於1h預測,非季節模型誤差有較大波動,改進後的模型,即卡爾曼濾波季節模型相對較為平穩。

　　總體來說季節模型預測精度相對較高。

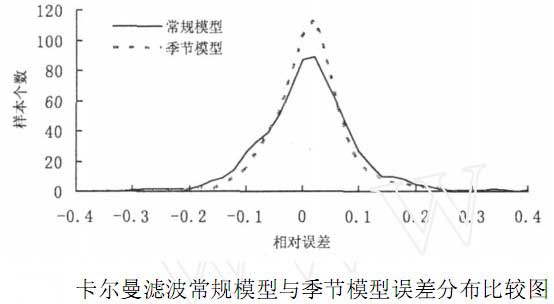
　　評價模型預測精度,還需查看其預測誤差分佈特征^[7]。

　　圖3為卡爾曼濾波常規模型與季節模型預測誤差分佈比較,採用了1個月數據,用2種方法進行了預測,從圖中可以看出,2種方法誤差都主要集中在-0.1至0.1區域,呈對稱分佈。從1個月所有數據來看,誤差大致呈正態分佈,季節模型較常規模型趨勢圖更為尖銳,表明季節模型比常規模型預測效果更為理想。綜合上圖和下圖,比較得出,卡爾曼濾波季節模型具有更高的預測精度。

　　採用基於卡爾曼濾波方法預測模型,進行時用水量預測。鑒於城市時用水量具有周期性、趨勢性及隨機擾動性,引入季節因數,形成卡爾曼濾波方法季節模型。以杭州市實測數據為例,分別採用卡爾曼濾波模型和卡爾曼濾波季節模型分別對該市時用水量進行預測,預測結果表明,卡爾曼濾波方法季節預測模型精度相對較高。從計算模型看,季節預測模型要求低,但預測精度較高,具有一定實用性,能夠滿足供水系統優化調度的要求。