灰色關聯分析
出自 MBA智库百科(https://wiki.mbalib.com/)
灰色關聯分析(Grey Relational Analysis, GRA)
目錄 |
灰色關聯分析是指對一個系統發展變化態勢的定量描述和比較的方法,其基本思想是通過確定參考數據列和若幹個比較數據列的幾何形狀相似程度來判斷其聯繫是否緊密,它反映了曲線間的關聯程度[1]。
在系統發展過程中,若兩個因素變化的趨勢具有一致性,即同步變化程度較高,即可謂二者關聯程度較高;反之,則較低。因此,灰色關聯分析方法,是根據因素之間發展趨勢的相似或相異程度,亦即“灰色關聯度”,作為衡量因素間關聯程度的一種方法。
灰色系統理論提出了對各子系統進行灰色關聯度分析的概念,意圖透過一定的方法,去尋求系統中各子系統(或因素)之間的數值關係。因此,灰色關聯度分析對於一個系統發展變化態勢提供了量化的度量,非常適合動態歷程分析。
通常可以運用此方法來分析各個因素對於結果的影響程度,也可以運用此方法解決隨時間變化的綜合評價類問題,其核心是按照一定規則確立隨時間變化的母序列,把各個評估對象隨時間的變化作為子序列,求各個子序列與母序列的相關程度,依照相關性大小得出結論。
灰色系統理論是由著名學者鄧聚龍教授首創的一種系統科學理論(Grey Theory),其中的灰色關聯分析是根據各因素變化曲線幾何形狀的相似程度,來判斷因素之間關聯程度的方法。
此方法通過對動態過程發展態勢的量化分析,完成對系統內時間序列有關統計數據幾何關係的比較,求出參考數列與各比較數列之間的灰色關聯度。與參考數列關聯度越大的比較數列,其發展方向和速率與參考數列越接近,與參考數列的關係越緊密。
灰色關聯分析方法要求樣本容量可以少到4個,對數據無規律同樣適用,不會出現量化結果與定性分析結果不符的情況。其基本思想是將評價指標原始觀測數進行無量綱化處理,計算關聯繫數、關聯度以及根據關聯度的大小對待評指標進行排序。
灰色關聯度的應用涉及社會科學和自然科學的各個領域,尤其在社會經濟領域,如國民經濟各部門投資收益、區域經濟優勢分析、產業結構調整等方面,都取得較好的應用效果。[2]
關聯度有絕對關聯度和相對關聯度之分,絕對關聯度採用初始點零化法進行初值化處理,當分析的因素差異較大時,由於變數間的量綱不一致,往往影響分析,難以得出合理的結果。而相對關聯度用相對量進行分析,計算結果僅與序列相對於初始點的變化速率有關,與各觀測數據大小無關,這在一定程度上彌補了絕對關聯度的缺陷。[2]
灰色關聯分析的計算步驟[2]
灰色關聯分析的具體計算步驟如下:
第一步:確定分析數列。
確定反映系統行為特征的參考數列和影響系統行為的比較數列。反映系統行為特征的數據序列,稱為參考數列。影響系統行為的因素組成的數據序列,稱比較數列。
設參考數列(又稱母序列)為Y={Y(k) | k = 1,2,Λ,n};比較數列(又稱子序列)Xi={Xi(k) | k = 1,2,Λ,n},i = 1,2,Λ,m。
第二步,變數的無量綱化
由於系統中各因素列中的數據可能因量綱不同,不便於比較或在比較時難以得到正確的結論。因此在進行灰色關聯度分析時,一般都要進行數據的無量綱化處理。
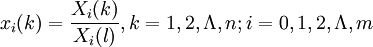
第三步,計算關聯繫數
x0(k)與xi(k)的關聯繫數
記 ,則
,則
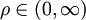 ,稱為分辨繫數。ρ越小,分辨力越大,一般ρ的取值區間為(0,1),具體取值可視情況而定。當
,稱為分辨繫數。ρ越小,分辨力越大,一般ρ的取值區間為(0,1),具體取值可視情況而定。當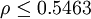 時,分辨力最好,通常取ρ = 0.5。
時,分辨力最好,通常取ρ = 0.5。
第四步,計算關聯度
因為關聯繫數是比較數列與參考數列在各個時刻(即曲線中的各點)的關聯程度值,所以它的數不止一個,而信息過於分散不便於進行整體性比較。因此有必要將各個時刻(即曲線中的各點)的關聯繫數集中為一個值,即求其平均值,作為比較數列與參考數列間關聯程度的數量表示,關聯度ri公式如下:
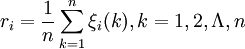
第五步,關聯度排序
關聯度按大小排序,如果r1 < r2,則參考數列y與比較數列x2更相似。
在算出Xi(k)序列與Y(k)序列的關聯繫數後,計算各類關聯繫數的平均值,平均值ri就稱為Y(k)與Xi(k)的關聯度。
例1:
下表為某地區國內生產總值的統計數據(以百萬元計),問該地區從2000年到2005年之間哪一種產業對GDP總量影響最大。
| 年份 | 國內生產總值 | 第一產業 | 第二產業 | 第三產業 |
| 2000 | 1988 | 386 | 839 | 763 |
| 2001 | 2061 | 408 | 846 | 808 |
| 2002 | 2335 | 422 | 960 | 953 |
| 2003 | 2750 | 482 | 1258 | 1010 |
| 2004 | 3356 | 511 | 1577 | 1268 |
| 2005 | 3806 | 561 | 1893 | 1352 |
步驟1:確立母序列,在此需要分別將三種產業與國內生產總值比較計算其關聯程度,故母序列為國內生產總值。若是解決綜合評價問題時則母序列可能需要自己生成,通常選定每個指標或時間段中所有子序列中的最佳值組成的新序列為母序列。
步驟2:無量綱化處理,在此採用均值化法,即將各個序列每年的統計值與整條序列的均值作比值,可以得到如下結果:
| 年份 | 國內生產總值 | 第一產業 | 第二產業 | 第三產業 |
| 2000 | 0.7320 | 0.8361 | 0.6828 | 0.7439 |
| 2001 | 0.7588 | 0.8838 | 0.6885 | 0.7878 |
| 2002 | 0.8597 | 0.9141 | 0.7812 | 0.9292 |
| 2003 | 1.0125 | 1.0440 | 1.0237 | 0.9847 |
| 2004 | 1.2356 | 1.1069 | 1.2833 | 1.2363 |
| 2005 | 1.4013 | 1.2152 | 1.5405 | 1.3182 |
步驟3:計算每個子序列中各項參數與母序列對應參數的關聯繫數,運用公式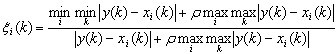 ,其中Kij表示第i個子序列的第j個參數與母序列(即0序列)的第j個參數的關聯繫數,p為分辨繫數取值範圍在[0,1],其取值越小求得的關聯繫數之間的差異性越顯著,在此取為0.5進行計算可得到如下結果:
,其中Kij表示第i個子序列的第j個參數與母序列(即0序列)的第j個參數的關聯繫數,p為分辨繫數取值範圍在[0,1],其取值越小求得的關聯繫數之間的差異性越顯著,在此取為0.5進行計算可得到如下結果:
| 年份t | S01(t) | S02(t) | S03(t) |
| 2000 | 0.4755 | 0.6591 | 0.8933 |
| 2001 | 0.4299 | 0.5739 | 0.7681 |
| 2002 | 0.6358 | 0.5465 | 0.5767 |
| 2003 | 0.7527 | 0.8993 | 0.7758 |
| 2004 | 0.4228 | 0.6661 | 1.0000 |
| 2005 | 0.3358 | 0.4037 | 0.5322 |
步驟4:計算關聯度,用公式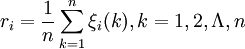 ,
可以得到r01 = 0.5088r02 = 0.6248r03 = 0.7577,通過比較三個子序列與母序列的關聯度可以得出結論:該地區在2000年到2005年期間的國內生產總值受到第三產業的影響最大。
,
可以得到r01 = 0.5088r02 = 0.6248r03 = 0.7577,通過比較三個子序列與母序列的關聯度可以得出結論:該地區在2000年到2005年期間的國內生產總值受到第三產業的影響最大。
例2
山西省汾河上游的輸沙量與降雨徑流的灰色關聯分析汾河是山西省的主要河流,在汾河下游距太原市100多公裡的西山修建了汾河水庫。該水庫不但對農業灌溉、防洪蓄水、魚類養殖等起著很大作用,並且還為太原市的用水提供了保證。建庫以來,人們經常在考慮如何防止庫容被泥沙淤塞,使水庫能長期有效為工農業生產與人民生活服務。 影響泥沙輸入水庫的因素較多,比如降雨量、徑流量、植被覆蓋率等。在這些因素中哪些是主要的,哪些是次要的有待研究和量化分析。
根據關聯繫數求關聯度得
r1=0.41(年徑流量與輸沙量的關聯程度)
r2=0.21(年平均降雨量與輸沙量的關聯程度)
r3=0.23(平均汛期降雨量與輸沙量的關聯程度)
相應的關聯序為r1>r3>r2
上述關聯序表明對輸沙量影響最大的是年徑流量,其次是汛期降雨量,再其次是平均年降雨量。
實際上,強度大的暴雨沖刷力大,難以被土壤吸收,從而在地表形成徑流,造成水土流失,引起河道泥沙流量的形成而暴雨又大多在汛期,因此徑流量是引起河道輸沙的綜合因素,所以徑流量大反映了雨強大,反映了水土保持較差,反映了水土流失較嚴重,反映了汛期雨量較大。而汛期的降雨量可能是雨強較大的的降雨量,也可能是雨強較小的降雨量。而平均年降雨量則與雨強、水土保持、水土流失無直接關係。
評論(共11條)
這個參考文獻怎麼感覺怪怪的,是不是亂編的啊
MBA智庫百科的參考文獻均是有相應出處的。您可以進行進一步查證
這個參考文獻怎麼感覺怪怪的,是不是亂編的啊
我也覺得好怪在看venture capital investment selection decesion-making base on fuzzy throey時看到grey rational analysis . 看完後沒明白這是怎麼回事。。
不准確
在條目中舉了個相關例子,可以學習理解~
我在知網也沒搜到第二篇參考文獻
我在知網也沒搜到第二篇參考文獻
您好!第二篇參考文獻在原創力文檔中可以查看到








這個參考文獻怎麼感覺怪怪的,是不是亂編的啊