灰色关联分析
出自 MBA智库百科(https://wiki.mbalib.com/)
灰色关联分析(Grey Relational Analysis, GRA)
目录 |
灰色关联分析是指对一个系统发展变化态势的定量描述和比较的方法,其基本思想是通过确定参考数据列和若干个比较数据列的几何形状相似程度来判断其联系是否紧密,它反映了曲线间的关联程度[1]。
在系统发展过程中,若两个因素变化的趋势具有一致性,即同步变化程度较高,即可谓二者关联程度较高;反之,则较低。因此,灰色关联分析方法,是根据因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。
灰色系统理论提出了对各子系统进行灰色关联度分析的概念,意图透过一定的方法,去寻求系统中各子系统(或因素)之间的数值关系。因此,灰色关联度分析对于一个系统发展变化态势提供了量化的度量,非常适合动态历程分析。
通常可以运用此方法来分析各个因素对于结果的影响程度,也可以运用此方法解决随时间变化的综合评价类问题,其核心是按照一定规则确立随时间变化的母序列,把各个评估对象随时间的变化作为子序列,求各个子序列与母序列的相关程度,依照相关性大小得出结论。
灰色系统理论是由著名学者邓聚龙教授首创的一种系统科学理论(Grey Theory),其中的灰色关联分析是根据各因素变化曲线几何形状的相似程度,来判断因素之间关联程度的方法。
此方法通过对动态过程发展态势的量化分析,完成对系统内时间序列有关统计数据几何关系的比较,求出参考数列与各比较数列之间的灰色关联度。与参考数列关联度越大的比较数列,其发展方向和速率与参考数列越接近,与参考数列的关系越紧密。
灰色关联分析方法要求样本容量可以少到4个,对数据无规律同样适用,不会出现量化结果与定性分析结果不符的情况。其基本思想是将评价指标原始观测数进行无量纲化处理,计算关联系数、关联度以及根据关联度的大小对待评指标进行排序。
灰色关联度的应用涉及社会科学和自然科学的各个领域,尤其在社会经济领域,如国民经济各部门投资收益、区域经济优势分析、产业结构调整等方面,都取得较好的应用效果。[2]
关联度有绝对关联度和相对关联度之分,绝对关联度采用初始点零化法进行初值化处理,当分析的因素差异较大时,由于变量间的量纲不一致,往往影响分析,难以得出合理的结果。而相对关联度用相对量进行分析,计算结果仅与序列相对于初始点的变化速率有关,与各观测数据大小无关,这在一定程度上弥补了绝对关联度的缺陷。[2]
灰色关联分析的计算步骤[2]
灰色关联分析的具体计算步骤如下:
第一步:确定分析数列。
确定反映系统行为特征的参考数列和影响系统行为的比较数列。反映系统行为特征的数据序列,称为参考数列。影响系统行为的因素组成的数据序列,称比较数列。
设参考数列(又称母序列)为Y={Y(k) | k = 1,2,Λ,n};比较数列(又称子序列)Xi={Xi(k) | k = 1,2,Λ,n},i = 1,2,Λ,m。
第二步,变量的无量纲化
由于系统中各因素列中的数据可能因量纲不同,不便于比较或在比较时难以得到正确的结论。因此在进行灰色关联度分析时,一般都要进行数据的无量纲化处理。
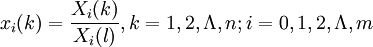
第三步,计算关联系数
x0(k)与xi(k)的关联系数
记 ,则
,则
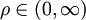 ,称为分辨系数。ρ越小,分辨力越大,一般ρ的取值区间为(0,1),具体取值可视情况而定。当
,称为分辨系数。ρ越小,分辨力越大,一般ρ的取值区间为(0,1),具体取值可视情况而定。当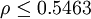 时,分辨力最好,通常取ρ = 0.5。
时,分辨力最好,通常取ρ = 0.5。
第四步,计算关联度
因为关联系数是比较数列与参考数列在各个时刻(即曲线中的各点)的关联程度值,所以它的数不止一个,而信息过于分散不便于进行整体性比较。因此有必要将各个时刻(即曲线中的各点)的关联系数集中为一个值,即求其平均值,作为比较数列与参考数列间关联程度的数量表示,关联度ri公式如下:
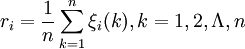
第五步,关联度排序
关联度按大小排序,如果r1 < r2,则参考数列y与比较数列x2更相似。
在算出Xi(k)序列与Y(k)序列的关联系数后,计算各类关联系数的平均值,平均值ri就称为Y(k)与Xi(k)的关联度。
例1:
下表为某地区国内生产总值的统计数据(以百万元计),问该地区从2000年到2005年之间哪一种产业对GDP总量影响最大。
| 年份 | 国内生产总值 | 第一产业 | 第二产业 | 第三产业 |
| 2000 | 1988 | 386 | 839 | 763 |
| 2001 | 2061 | 408 | 846 | 808 |
| 2002 | 2335 | 422 | 960 | 953 |
| 2003 | 2750 | 482 | 1258 | 1010 |
| 2004 | 3356 | 511 | 1577 | 1268 |
| 2005 | 3806 | 561 | 1893 | 1352 |
步骤1:确立母序列,在此需要分别将三种产业与国内生产总值比较计算其关联程度,故母序列为国内生产总值。若是解决综合评价问题时则母序列可能需要自己生成,通常选定每个指标或时间段中所有子序列中的最佳值组成的新序列为母序列。
步骤2:无量纲化处理,在此采用均值化法,即将各个序列每年的统计值与整条序列的均值作比值,可以得到如下结果:
| 年份 | 国内生产总值 | 第一产业 | 第二产业 | 第三产业 |
| 2000 | 0.7320 | 0.8361 | 0.6828 | 0.7439 |
| 2001 | 0.7588 | 0.8838 | 0.6885 | 0.7878 |
| 2002 | 0.8597 | 0.9141 | 0.7812 | 0.9292 |
| 2003 | 1.0125 | 1.0440 | 1.0237 | 0.9847 |
| 2004 | 1.2356 | 1.1069 | 1.2833 | 1.2363 |
| 2005 | 1.4013 | 1.2152 | 1.5405 | 1.3182 |
步骤3:计算每个子序列中各项参数与母序列对应参数的关联系数,运用公式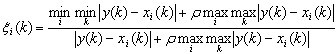 ,其中Kij表示第i个子序列的第j个参数与母序列(即0序列)的第j个参数的关联系数,p为分辨系数取值范围在[0,1],其取值越小求得的关联系数之间的差异性越显著,在此取为0.5进行计算可得到如下结果:
,其中Kij表示第i个子序列的第j个参数与母序列(即0序列)的第j个参数的关联系数,p为分辨系数取值范围在[0,1],其取值越小求得的关联系数之间的差异性越显著,在此取为0.5进行计算可得到如下结果:
| 年份t | S01(t) | S02(t) | S03(t) |
| 2000 | 0.4755 | 0.6591 | 0.8933 |
| 2001 | 0.4299 | 0.5739 | 0.7681 |
| 2002 | 0.6358 | 0.5465 | 0.5767 |
| 2003 | 0.7527 | 0.8993 | 0.7758 |
| 2004 | 0.4228 | 0.6661 | 1.0000 |
| 2005 | 0.3358 | 0.4037 | 0.5322 |
步骤4:计算关联度,用公式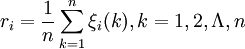 ,
可以得到r01 = 0.5088r02 = 0.6248r03 = 0.7577,通过比较三个子序列与母序列的关联度可以得出结论:该地区在2000年到2005年期间的国内生产总值受到第三产业的影响最大。
,
可以得到r01 = 0.5088r02 = 0.6248r03 = 0.7577,通过比较三个子序列与母序列的关联度可以得出结论:该地区在2000年到2005年期间的国内生产总值受到第三产业的影响最大。
例2
山西省汾河上游的输沙量与降雨径流的灰色关联分析汾河是山西省的主要河流,在汾河下游距太原市100多公里的西山修建了汾河水库。该水库不但对农业灌溉、防洪蓄水、鱼类养殖等起着很大作用,并且还为太原市的用水提供了保证。建库以来,人们经常在考虑如何防止库容被泥沙淤塞,使水库能长期有效为工农业生产与人民生活服务。 影响泥沙输入水库的因素较多,比如降雨量、径流量、植被覆盖率等。在这些因素中哪些是主要的,哪些是次要的有待研究和量化分析。
根据关联系数求关联度得
r1=0.41(年径流量与输沙量的关联程度)
r2=0.21(年平均降雨量与输沙量的关联程度)
r3=0.23(平均汛期降雨量与输沙量的关联程度)
相应的关联序为r1>r3>r2
上述关联序表明对输沙量影响最大的是年径流量,其次是汛期降雨量,再其次是平均年降雨量。
实际上,强度大的暴雨冲刷力大,难以被土壤吸收,从而在地表形成径流,造成水土流失,引起河道泥沙流量的形成而暴雨又大多在汛期,因此径流量是引起河道输沙的综合因素,所以径流量大反映了雨强大,反映了水土保持较差,反映了水土流失较严重,反映了汛期雨量较大。而汛期的降雨量可能是雨强较大的的降雨量,也可能是雨强较小的降雨量。而平均年降雨量则与雨强、水土保持、水土流失无直接关系。
评论(共11条)
这个参考文献怎么感觉怪怪的,是不是乱编的啊
MBA智库百科的参考文献均是有相应出处的。您可以进行进一步查证
这个参考文献怎么感觉怪怪的,是不是乱编的啊
我也觉得好怪在看venture capital investment selection decesion-making base on fuzzy throey时看到grey rational analysis . 看完后没明白这是怎么回事。。
不准确
在条目中举了个相关例子,可以学习理解~
我在知网也没搜到第二篇参考文献
我在知网也没搜到第二篇参考文献
您好!第二篇参考文献在原创力文档中可以查看到








这个参考文献怎么感觉怪怪的,是不是乱编的啊