永續年金現值
出自 MBA智库百科(https://wiki.mbalib.com/)
永續年金現值(present value of perpetual annuity)
目錄 |
什麼是永續年金現值[1]
永續年金現值是指無限期地每期期末等額收付系列款項的複利現值之和。
永續年金現值的基本計算公式[2]
永續年金是無限期支付的年金,無終值。在現實經濟生活中,永續年金是不存在的,但期限長、利率高的年金,可以視同永續年金,用永續年金現值計算方法計算其近似現值。我們將年金間隔期與計息期一致的永續年金稱為一般永續年金或標準永續年金,年金間隔期與計息期不一致的永續年金稱為特殊永續年金或非標準永續年金。一般永續年金現值計劃公式稱為計算永續年金現值的基本公式(以下簡稱為基本公式)。由於計息期一般為一年,所以我們以計息期一年為例。
設某間隔期為一年的永續年金為R,年折現率為i,現值為V0。根據普通年金現值計算公式有: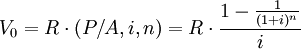
當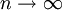 時,
時, 為0。
為0。
於是得到基本公式為: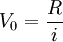
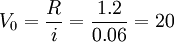 (元)
(元)當股票價值大於價格時,預期報酬率大於最低報酬率,投資該股票合算;反之,則不合算。
特殊永續年金現值的分析和運用[2]
特殊永續年金可分為年金間隔期大於計息期的永續年金和年金間隔期小於計息期的永續年金兩種。由於特殊永續年金的間隔期與計息期不同,所以必須首先將年金和折現率換算成同期限的值,再套用基本公式計算現值。
(1)年金間隔期大於計息期的永續年金現值的分析和運用。以計息期一年為例,設某間隔期為m年(m>1)的永續年金為R',年折現率為i,其現值為V0。
計算V0的方法有三種:
1.每次年金R'等於每年取出利息另外存入銀行的m年的普通年金終值。每年利息為V0xi,其m年的普通年金終值為V0xix(F/A,i,m)。於是: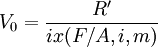

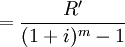
2.將每m年看作一個整體,R'為這個整體的終值,通過計算積累基金的辦法將所有間隔二年的永續年金R'換算為間隔一年的永續年金R,再套用基本公式求其現值。
即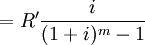
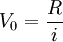
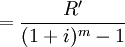
3.以m年為一個期間,在這個期間內複利m次,每次利率為i,則其名義利率為mi。利用名義利率和真實利率換算的方法,將年折現率i調整到m年的真實利率i',再套用基本公式求現值。
即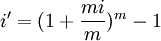

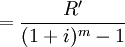
可見,上述三種方法是從不同途徑考慮問題,其計算結果是一致的。
例如,某學校準備籌集一筆基金存入銀行,以便以後每過4年頒發一次特別獎金,每次獎金為18000元,銀行存款利率為8%,按年複利計算求這筆基金的數額。
根據前面分析結果,可以計算這筆基金數額為:
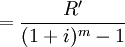

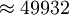 (元)
(元)(2)年金間隔期小於計息期的永續年金現值的分析和運用。以計息期一年為例,設某間隔期為n年(n<1)的永續年金為R",年折現率為i,現值為V0。計算V0的方法也有三種。
1.每次年金為R",等於每n年取出利息,n年的利息為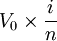 。
。
於是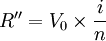 ,則
,則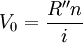
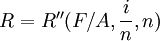
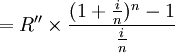
![=\frac{R''n}{i} \times [(1+\frac{i}{n})^n-1]](/w/images/math/d/7/7/d77b502828954baf4ebf3df799b4aef0.png)
同時,將年名義利率i換算成年真實利率i",即
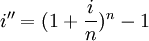
則R與i"期限相同,套用基本公式有:
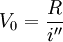
![=\frac{\frac{R'' \times n}{i} \times [(1+\frac{i}{n})^n-1]}{(1+\frac{i}{n})^n-1}](/w/images/math/4/3/9/4391020661a18d113f6f5f5a806fb718.png)
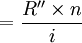
3.由於每次利息取出,不存在利息再計息,則n年的利息率為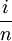 ,此時R"與
,此時R"與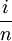 期限相同,套用基本公式有:
期限相同,套用基本公式有:
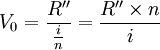
三種方法計算結果仍是相同的。
例如,某廠準備買入一張保險單,以便今後每月從保險公司取出10000元用於發放退休職工工資,年利率為6%,按複利計算這張保險單的價格。
根據前面分析結果,可以計算這張保險單的價格為: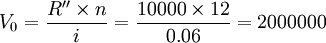 (元)
(元)







推理步驟很好