永续年金现值
出自 MBA智库百科(https://wiki.mbalib.com/)
永续年金现值(present value of perpetual annuity)
目录 |
什么是永续年金现值[1]
永续年金现值是指无限期地每期期末等额收付系列款项的复利现值之和。
永续年金现值的基本计算公式[2]
永续年金是无限期支付的年金,无终值。在现实经济生活中,永续年金是不存在的,但期限长、利率高的年金,可以视同永续年金,用永续年金现值计算方法计算其近似现值。我们将年金间隔期与计息期一致的永续年金称为一般永续年金或标准永续年金,年金间隔期与计息期不一致的永续年金称为特殊永续年金或非标准永续年金。一般永续年金现值计划公式称为计算永续年金现值的基本公式(以下简称为基本公式)。由于计息期一般为一年,所以我们以计息期一年为例。
设某间隔期为一年的永续年金为R,年折现率为i,现值为V0。根据普通年金现值计算公式有: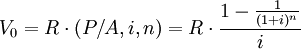
当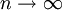 时,
时, 为0。
为0。
于是得到基本公式为: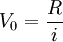
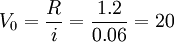 (元)
(元)当股票价值大于价格时,预期报酬率大于最低报酬率,投资该股票合算;反之,则不合算。
特殊永续年金现值的分析和运用[2]
特殊永续年金可分为年金间隔期大于计息期的永续年金和年金间隔期小于计息期的永续年金两种。由于特殊永续年金的间隔期与计息期不同,所以必须首先将年金和折现率换算成同期限的值,再套用基本公式计算现值。
(1)年金间隔期大于计息期的永续年金现值的分析和运用。以计息期一年为例,设某间隔期为m年(m>1)的永续年金为R',年折现率为i,其现值为V0。
计算V0的方法有三种:
1.每次年金R'等于每年取出利息另外存入银行的m年的普通年金终值。每年利息为V0xi,其m年的普通年金终值为V0xix(F/A,i,m)。于是: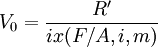

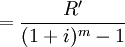
2.将每m年看作一个整体,R'为这个整体的终值,通过计算积累基金的办法将所有间隔二年的永续年金R'换算为间隔一年的永续年金R,再套用基本公式求其现值。
即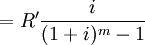
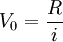
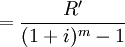
3.以m年为一个期间,在这个期间内复利m次,每次利率为i,则其名义利率为mi。利用名义利率和真实利率换算的方法,将年折现率i调整到m年的真实利率i',再套用基本公式求现值。
即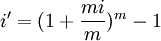

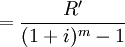
可见,上述三种方法是从不同途径考虑问题,其计算结果是一致的。
例如,某学校准备筹集一笔基金存入银行,以便以后每过4年颁发一次特别奖金,每次奖金为18000元,银行存款利率为8%,按年复利计算求这笔基金的数额。
根据前面分析结果,可以计算这笔基金数额为:
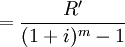

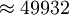 (元)
(元)(2)年金间隔期小于计息期的永续年金现值的分析和运用。以计息期一年为例,设某间隔期为n年(n<1)的永续年金为R",年折现率为i,现值为V0。计算V0的方法也有三种。
1.每次年金为R",等于每n年取出利息,n年的利息为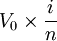 。
。
于是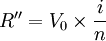 ,则
,则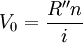
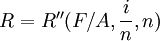
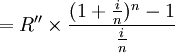
![=\frac{R''n}{i} \times [(1+\frac{i}{n})^n-1]](/w/images/math/d/7/7/d77b502828954baf4ebf3df799b4aef0.png)
同时,将年名义利率i换算成年真实利率i",即
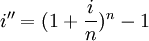
则R与i"期限相同,套用基本公式有:
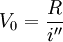
![=\frac{\frac{R'' \times n}{i} \times [(1+\frac{i}{n})^n-1]}{(1+\frac{i}{n})^n-1}](/w/images/math/4/3/9/4391020661a18d113f6f5f5a806fb718.png)
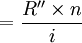
3.由于每次利息取出,不存在利息再计息,则n年的利息率为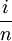 ,此时R"与
,此时R"与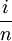 期限相同,套用基本公式有:
期限相同,套用基本公式有:
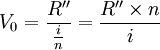
三种方法计算结果仍是相同的。
例如,某厂准备买入一张保险单,以便今后每月从保险公司取出10000元用于发放退休职工工资,年利率为6%,按复利计算这张保险单的价格。
根据前面分析结果,可以计算这张保险单的价格为: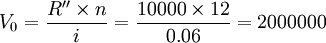 (元)
(元)







推理步骤很好