死亡率模型
出自 MBA智库百科(https://wiki.mbalib.com/)
死亡率模型（Mortality model）
目錄 |
阿爾特曼(Altman)的死亡率模型(mortality models)是依據壽險思路所開發的，即該模型與確定壽險保費時的方法和思路一致。它以債券或貸款在特定時間段的違約率的組合為基礎，根據信用等級分類，開發出一張表格(稱之為死亡率表),用該表對債券或貸款的一年的邊際死亡率(marginal mortality rate。MMR)和多年的累計死亡率(cumulative motality rate，CMR)進行預測，衡量某個特定信用等級的債券或者貸款的違約率。
該模型認為各債券違約相互獨立，即不存在相關效應和連鎖反應，相同信用等級的債券違約情況相同，而不同債券類型的違約下的損失率不同且相互獨立，但同一債券類型的違約下的損失率基本相同，這些與信用度量術有相同之處，但兩種模型在處理上有明顯不同。
事實上，該模型是用歷史數據統計不同信用等級下債券的邊際死亡率和累計死亡率，同時，也可以統計出不同信用等級下的LGD，所以該方法比較容易理解，但應用也存在較大難度，主要是對數據量要求很大，許多單個商業銀行無法提供如此大的資料庫，如對有7個信用等級的債券的損失進行比較精確測算，則樣本要達到 7萬多個，這對一般商業銀行是不可能的。
死亡率模型的內容[1]
死亡率模型的應用範圍包括債券和貸款，但是由於缺乏足夠規模的貸款違約資料庫，該模型的發展受到了很大的阻力。某個特定信用等級為i的債券在t年的邊際死亡率(MMR)的 計算公式如下：
|
MMRt＝ | 在t年違約的j級債券的總額 | |
| t年初樣本中j級債券的總額 |
計算出個別年份的MMR後， 通過計算MMRt的加權平均值帶入死亡率表中。所使用的權重ω應該反映不同年份中的相對發行規模．因而結果會偏向於發行規模大的年份，這樣是正確的。例如，求從發行(n年)後兩年內某一特定級別j的債券的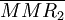
的計算公式為：
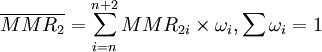
計算債券或貸款超過1年的違約概率的累計死亡率(CMR)要用到存活率(survival rate，SR)。
t年的存活率SR的計算公式為：SRt = l − MMRt。；累計死亡率(CMR)是對某個時間段而言的，其計算等式為：
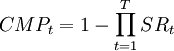
T表示計算累計死亡率所包括的總的時間段。
該模型的主要優勢：比較容易利用死亡率表來計算單個債券和債券組合的預期損失及其波動率，特別是計算債券組合很方便；死亡模型是從大量樣本中統計出來的一個模型，所以採用的參數比較少。
該模型主要劣勢：沒有考慮不同債券的相關性對計算結果的影響；沒有考慮巨集觀經濟環境對死亡率的影響，因而需要時時更新死亡率表；數據更新和計算量很大；不能處理非線性產品，如期權、外幣掉期
案例一:商業銀行死亡率模型分析[2]
客戶不能正常歸還貸款的可能性即客戶違約率。對某一客戶的某一筆貸款而言，要麼違約，要麼不違約，沒有違約比例的問題，但對某一類客戶(如同一信用等級的客戶)而言．或對同一客戶的多筆貸款而言．就有一個違約比例的問題。目前常用的商業銀行信用風險模型主要有三類：一是基於公司價值的J．P摩根的信用計量CredjtMetrics和KMV模型；二是基於經濟學的Mckinsey的Credit Portfolio View；三是基於保險精算的CSFP的Creditkisk。以壽險精算中的死亡率模型來測度客戶違約率。
二、壽險精算中的死亡率模則
壽險精算中死亡率模型描述人口在整數年齡上存活和死亡的規律，年齡是人出生後存活時間的度量，是一個連續隨機變數。假設新生兒未來存活時間或者說新生兒的死亡年齡為X，它是一個連續的隨機變數。其分佈函數為：
F(x) = Pr(X > x),x≥0。
它是新生兒在x歲前死亡的概率。
設S(x) = 1 − F(x) = Pr(X > x),x≥0。
它是新生兒活到x歲的概率，S(x)稱為生存函數
死亡力是描述瞬間死亡水平的指標，定義為：
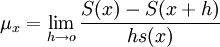
x歲的人在t時間記憶體活的概率: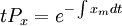
x歲的人在x-x+m歲死亡的概率: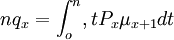
三、死亡率模型引入至商業銀行風險量化管理
無論信用風險發生的原因如何，但從結果來看，可分為違約和不違約兩種情況，對股子壽險精算中的死亡和生存兩種狀態。由於人的死亡與借款人的違約現象具有一定的相似性，亦即人的死亡率解析分佈與信貸違約概率分佈具有一定的相似性，因此，可以利用壽險精算中死亡率模型分析方法來定撤研究商業銀行借款人的違約概率，並以此為依據測算商業銀行貸款的違約損失，揭示商業銀行信用風險發生的數量規律。利用死亡率模型研究商業銀行信用風險具有一定的科學性和可靠度。
1.客戶違約惑與信用評級
利用統計方法分析歷史數據信用評級機構或商業銀行自身計算出每年度對班子評級分類的違約率(即死亡率)。同時，計算不同評級分類狀態的轉移矩陣，反映經濟形勢變化發生的不同時期年度違約率的波動性。
客戶年度違約率與信用評級
| 信用評級 | 客戶年度違約率 |
| AAA | 0.02% |
| AA | 0.04% |
| A | 0.08% |
| BBB | 0.20% |
| BB | 1.80% |
| B | 8.30% |
| CCC | 28.80% |
不同的信用評級與其對應的違約率之間不存在比例關係。當信用評級下降時違約率但是指數增長，信用評級下降的過程是違約感急劇增加的過程。
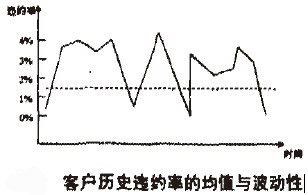
客戶違約率隨時間變化是不穩定的。用違約率解觀察值的標準差表示年度違約率率的歷史攪動性，當信用評級下降時，波動性隨違約率水平的提高而增加，這與當違約率低到接近零時違約率的變化空間也接近零的事實相符，利用不同時期觀察到的違約率時間序列可得到這樣的波動性。
違約率波動性是度最貸款組合意外損失的基礎。如果波動性高，違約率但潛在偏離均值的可能性就大;反之，這種潛在偏差的可能性就小，前者的意外損失較高。意外損失與違約率的標準差成正比例，而預期損失與平均違約旦郭成正比例。
2.客戶累積邊約率與借用評級轉移
累積的違約率隨時間長度的增加而增加，觀察的時期越長觀察到違約的機會越多(死亡率越高) ，但違約率(死亡率)隨時間長度的增加也不是成正比例的。借用i平級高的債務應約率低，但違約黎的增加率高，而借用評級低的債務違約率高，但違約率的增長率低。如果違約風險高的借款人生存的時間較伏，那麼他們肯定是降低了自身的風險才得以生存。
風險低的借款人隨著時間的錐移，其信用質量惡化的可能性人。辨別信用風險隨時間的變化，有利於評估借用的預期損失與非預期損失。
風險隨時間在不斷地變化，風險可能減少也可能增加。
轉移頻率表示評級分類之間的這些變化，把每個評級的變化頻率列表構造轉移矩陣，表示在給定的時期內，各個評級分分類之間的轉移比率(%)，如下表所示：
客戶信用評級一年期轉移矩陣
| 年末評級(%) | |||||||||
| 初始評級 | AAA | AA | A | BBB | BB | B | CCC | 違約 | |
| AAA | 90.81 | 8.33 | 0.68 | 0.06 | 0.12 | 0.00 | 0.00 | 0.00 | |
| AA | 0.70 | 90.65 | 1.79 | 0.64 | 0.06 | 0.14 | 0.02 | 0.00 | |
| A | 0.09 | 2.27 | 91.05 | 5.52 | 0.74 | 0.26 | 0.01 | 0.06 | |
| BBB | 0.02 | 0.33 | 5.95 | 86.93 | 5.3 | 1.17 | 1.12 | 0.18 | |
| BB | 0.03 | 0.14 | 0.67 | 7.73 | 80.53 | 8.84 | 1.00 | 1.06 | |
| B | 0.00 | 0.11 | 0.24 | 0.43 | 6.48 | 83.46 | 4.07 | 5.20 | |
| CCC | 0.22 | 0.00 | 0.22 | 1.30 | 2.38 | 11.24 | 64.86 | 19.79 | |
在相鄰評級之間最可能發生轉移，表現為高轉移概率集中在轉移矩陣的主對角線上。如標準瞥爾i平級為BBB的債權，到年來，其信用等級具有三種遷移路徑:
(1)保持當前的借用等級BBB；
(2) 向上遷移(從BBB級至A級)或向下遷移(從BBB級至BB級)；
(3)違約。轉移矩陣中的概率表示各種借用遷移情況發生的概率。
上表中BB日級的數字為BBB 級債權在1 年時間內保持借用評級不變，或者遷移到不同信用評級的概率。由下表中數據可知，一年來仍保持原來BBB 信用評級的概率為86.93% ，向上遷移到A級和下降到BB級的概率分別是5.95%和5。30%，在一年內違約的概率為0.18% 。
信用風險死亡率模型參數估計
| 信用等級 | x | 年度違約率 | y | x2 | xy |
| AAA | 1 | 0.0002 | -8.5172 | 1 | -8.5172 |
| AA | 2 | O.00O4 | -7.8240 | 4 | -15.6480 |
| A | 3 | 0.0008 | -7.1309 | 9 | -21.3927 |
| BBB | 4 | O.0020 | -6.2146 | 16 | -24.8584 |
| BB | 5 | 0.0180 | -4.0174 | 25 | -20.087 |
| B | 6 | 0.0830 | -2.4889 | 36 | -14.9334 |
| CCC | 7 | 0.2880 | -1.2448 | 49 | -8.7136 |
| 合計 | 28 | - | -37.4378 | 140 | -114.1503 |
四、商業銀行信用風險死亡率模型的擬合與應用
1.商業銀行信用風險死亡率模型的擬合及參數估計
從模型應用的廣泛性和實用性(參數不宜過多)等方商考貌5慮，假設死亡力按指數律增長，選擇指數曲線模型對商業銀行信用風險進行測度。
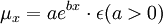(1)
其中，μx為信用等級x對應的客戶違約率，a、b為參數，\mu為隨機誤差項。
對模型(1)作線性變換，得到lnμx = lna + bx + lnε
令y = lnμ(x),A = lna,ε * = lnε
y = A + bx + ε *
(2)利用最小二乘法(LS)對模型(2)進行參數估計，得到模型擬合方程:
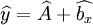
其中：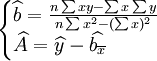
。
2.應用舉例
普爾公司某年度客戶違約率與信用(表)如下：
客戶累積違約概率(%)
| 期限 | 1 | 2 | 3 | 4 | 5… | 7… | 10… | 15 |
| AAA | 0.00 | 0.00 | 0.07 | 0.15 | 0.24 | 0.66 | 1.40 | 1.40 |
| AA | 0.00 | 0.02 | 0.12 | 0.25 | 0.43 | 0.89 | 1.29 | 1.48 |
| A | 0.06 | 0.16 | 0.27 | 0.44 | 0.67 | 1.12 | 2.17 | 3.00 |
| BBB | 0.18 | 0.44 | 0.72 | 1.21 | 1.78 | 2.99 | 4.34 | 4.70 |
| BB | 1.06 | 3.48 | 6.12 | 8.68 | 10.97 | 14.46 | 17.73 | 19.91 |
| B | 5.20 | 11.00 | 15.95 | 19.40 | 21.88 | 25.14 | 29.02 | 30.65 |
| CCC | 19.97 | 26.92 | 31.63 | 35.97 | 40.15 | 42.64 | 45.10 | 45.10 |
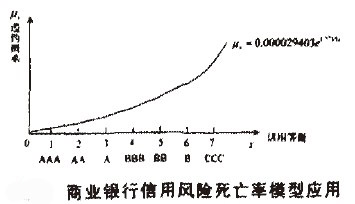
對商業銀行信用風險死亡率模型應用如下。
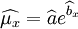
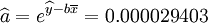
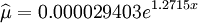
結果表明，該年度客戶違約率與信用評級之間的最化關係是x=0.000029403e1.2715x，即隨著借用評級等級的降低，客戶違約率呈指數增長。同時，在給定的時期內，利用商業銀行信用風險死亡率模型分析方法，可以根據部分借用等級客戶的違約率情況來估計其它信用等級客戶的違約率。
｀謝謝