時間序列預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
時間序列預測法(Time Series Forecasting Method)
目錄 |
一種歷史資料延伸預測,也稱歷史引伸預測法。是以時間數列所能反映的社會經濟現象的發展過程和規律性,進行引伸外推,預測其發展趨勢的方法。
時間序列,也叫時間數列、歷史複數或動態數列。它是將某種統計指標的數值,按時間先後順序排到所形成的數列。時間序列預測法就是通過編製和分析時間序列,根據時間序列所反映出來的發展過程、方向和趨勢,進行類推或延伸,藉以預測下一段時間或以後若幹年內可能達到的水平。其內容包括:收集與整理某種社會現象的歷史資料;對這些資料進行檢查鑒別,排成數列;分析時間數列,從中尋找該社會現象隨時間變化而變化的規律,得出一定的模式;以此模式去預測該社會現象將來的情況。
第一步 收集歷史資料,加以整理,編成時間序列,並根據時間序列繪成統計圖。時間序列分析通常是把各種可能發生作用的因素進行分類,傳統的分類方法是按各種因素的特點或影響效果分為四大類:(1)長期趨勢;(2)季節變動;(3)迴圈變動;(4)不規則變動。
第二步 分析時間序列。時間序列中的每一時期的數值都是由許許多多不同的因素同時發生作用後的綜合結果。
第三步 求時間序列的長期趨勢(T)季節變動(s)和不規則變動(I)的值,並選定近似的數學模式來代表它們。對於數學模式中的諸未知參數,使用合適的技術方法求出其值。
第四步 利用時間序列資料求出長期趨勢、季節變動和不規則變動的數學模型後,就可以利用它來預測未來的長期趨勢值T和季節變動值s,在可能的情況下預測不規則變動值I。然後用以下模式計算出未來的時間序列的預測值Y:
加法模式T+S+I=Y
乘法模式T×S×I=Y
如果不規則變動的預測值難以求得,就只求長期趨勢和季節變動的預測值,以兩者相乘之積或相加之和為時間序列的預測值。如果經濟現象本身沒有季節變動或不需預測分季分月的資料,則長期趨勢的預測值就是時間序列的預測值,即T=Y。但要註意這個預測值只反映現象未來的發展趨勢,即使很準確的趨勢線在按時間順序的觀察方面所起的作用,本質上也只是一個平均數的作用,實際值將圍繞著它上下波動。
時間序列分析基本特征[1]
1.時間序列分析法是根據過去的變化趨勢預測未來的發展,它的前提是假定事物的過去延續到未來。
時間序列分析,正是根據客觀事物發展的連續規律性,運用過去的歷史數據,通過統計分析,進一步推測未來的發展趨勢。事物的過去會延續到未來這個假設前提包含兩層含義:一是不會發生突然的跳躍變化,是以相對小的步伐前進;二是過去和當前的現象可能表明現在和將來活動的發展變化趨向。這就決定了在一般情況下,時間序列分析法對於短、近期預測比較顯著,但如延伸到更遠的將來,就會出現很大的局限性,導致預測值偏離實際較大而使決策失誤。
2.時間序列數據變動存在著規律性與不規律性
時間序列中的每個觀察值大小,是影響變化的各種不同因素在同一時刻發生作用的綜合結果。從這些影響因素髮生作用的大小和方向變化的時間特性來看,這些因素造成的時間序列數據的變動分為四種類型。
(1)趨勢性:某個變數隨著時間進展或自變數變化,呈現一種比較緩慢而長期的持續上升、下降、停留的同性質變動趨向,但變動幅度可能不相等。
(2)周期性:某因素由於外部影響隨著自然季節的交替出現高峰與低谷的規律。
(3)隨機性:個別為隨機變動,整體呈統計規律。
(4)綜合性:實際變化情況是幾種變動的疊加或組合。預測時設法過濾除去不規則變動,突出反映趨勢性和周期性變動。
時間序列預測法可用於短期預測、中期預測和長期預測。根據對資料分析方法的不同,又可分為:簡單序時平均數法、加權序時平均數法、移動平均法、加權移動平均法、趨勢預測法、指數平滑法、季節性趨勢預測法、市場壽命周期預測法等。
簡單序時平均數法 也稱算術平均法。即把若幹歷史時期的統計數值作為觀察值,求出算術平均數作為下期預測值。這種方法基於下列假設:“過去這樣,今後也將這樣”,把近期和遠期數據等同化和平均化,因此只能適用於事物變化不大的趨勢預測。如果事物呈現某種上升或下降的趨勢,就不宜採用此法。
加權序時平均數法 就是把各個時期的歷史數據按近期和遠期影響程度進行加權,求出平均值,作為下期預測值。
簡單移動平均法 就是相繼移動計算若幹時期的算術平均數作為下期預測值。
加權移動平均法 即將簡單移動平均數進行加權計算。在確定權數時,近期觀察值的權數應該大些,遠期觀察值的權數應該小些。
上述幾種方法雖然簡便,能迅速求出預測值,但由於沒有考慮整個社會經濟發展的新動向和其他因素的影響,所以準確性較差。應根據新的情況,對預測結果作必要的修正。
指數平滑法 即根據歷史資料的上期實際數和預測值,用指數加權的辦法進行預測。此法實質是由內加權移動平均法演變而來的一種方法,優點是只要有上期實際數和上期預測值,就可計算下期的預測值,這樣可以節省很多數據和處理數據的時間,減少數據的存儲量,方法簡便。是國外廣泛使用的一種短期預測方法。
季節趨勢預測法 根據經濟事物每年重覆出現的周期性季節變動指數,預測其季節性變動趨勢。推算季節性指數可採用不同的方法,常用的方法有季(月)別平均法和移動平均法兩種:a.季(月)別平均法。就是把各年度的數值分季(或月)加以平均,除以各年季(或月)的總平均數,得出各季(月)指數。這種方法可以用來分析生產、銷售、原材料儲備、預計資金周轉需要量等方面的經濟事物的季節性變動;b.移動平均法。即應用移動平均數計算比例求典型季節指數。
市場壽命周期預測法 就是對產品市場壽命周期的分析研究。例如對處於成長期的產品預測其銷售量,最常用的一種方法就是根據統計資料,按時間序列畫成曲線圖,再將曲線外延,即得到未來銷售發展趨勢。最簡單的外延方法是直線外延法,適用於對耐用消費品的預測。這種方法簡單、直觀、易於掌握。
案例一:可提費用的時間序列預測[2]
一、可提費用概述
可提費用是人壽保險保費收人中重要的組成部分,是目前國內人壽保險公司運營的基本保證。它的變化規律,對於保險公司的資金計劃、預算管理、以及發展規劃等行為起到至關重要的作用.因此合理、相對準確地預測可提費用對於保險公司在管理決策和發展規劃方面起到重要的作用。
可提費用與諸多因素有關,且這些因素多屬於不確定性因素,如:市場的成長性、客戶的持續繳費(選擇期繳方式的客戶)、季節性因素、新產品的開發與投放、央行的利率政策等,而且由於不同產品類型的收入規律和不同國家的經濟、社會水平不同,規律也不同,又因為人壽保險的產品保障類型組合非常複雜,統一的預測模式幾乎不可能實現.但研究結果表明,可提費用的逐月累計餘額構成的時間序列是一個有規則的周期波動,具有明顯的趨勢性和季節性,月度數據周期為12,這是由中國會計財年決定的(也有一些業務收入的月發生具有明顯的季節因素),利用季節模型還可有效刻畫年內的波動規律。
二、時間序列預測法
1.逐步自回歸(StepAR)模型:StepAR模型是有趨勢、季節因素數據的模型類。
2.Winters Method—Additive模型:它是將時勢和乘法季節因素相結合,考慮序列中有規律節波動。
3.ARlMA模型:它是處理帶有趨勢、季節因平穩隨機項數據的模型類[3]。
4.Winters Method—Muhiplicative模型:該方將時同趨勢和乘法季節因素相結合,考慮序列規律的季節波動。時間趨勢模型可根據該序列律的季節波動對該趨勢進行修正。為了能捕捉到季節性,趨勢模型包含每個季節的一個季節參季節因數採用乘法季節因數。隨機時間序列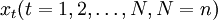 整理彙總歷史上各類保險的數據得到逐月的數據,Winters Method-Multiplicative模型表示為
整理彙總歷史上各類保險的數據得到逐月的數據,Winters Method-Multiplicative模型表示為
xt = (a + bt)s(t) + εt (1)
其中a和b為趨勢參數,s(t)為對應於時刻t的這個季節選擇的季節參數,修正方程為。
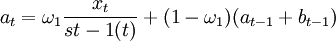 ,
,
bt = ω2(at − at − 1) + (1 − ω2)bt − 1 (2)
其中:xt,at,bt,分別為序列在時刻t的實測值、平滑值和平滑趨勢s{t-1}(t)選擇在季節因數被修正之前對應於時刻t的季節因數的過去值。
在該修正系統中,趨勢多項式在當前周期中總是被中心化,以便在t以後的時間里預報值的趨勢多項式的截距參數總是修正後的截距參數at。向前τ個周期的預報值是。
xt + τ = (at + btτ)st(t + τ)(3)
當季節在數據中改變時季節參數被修正,它使用季節實測值與預報值比率的平均值。
5.GARCH(ARCH)模型
帶自相關擾動的回歸模型為。
xt = ξtβ + vt,
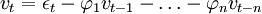 ,
,
εt = N(0,σ2) (4)
其中:xt為因變數;ξt為回歸因數構成的列向量;\beta為結構參數構成的列向量;εt為均值是0、方差是一的獨立同分佈正態隨機變數。
服從GARCH過程的序列xt,對於t時刻X的條件分佈記為
xt | φt − 1˜N(0,ht) (5)
其中\phi_{t-1}表示時間t-1前的所有可用信息,條件方差。
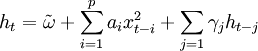 (6)。
(6)。
其中p≥0,q>0,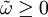 ,
,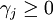 。
。
當p=0時,GARCH(p,q)模型退化為ARCH(p)模型,ARCH參數至少要有一個不為0。
GARCH回歸模型可寫成
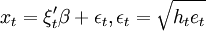 ,
,
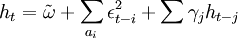 ,
,
et˜ N(0,1) (7)
也可以考慮服從自回歸過程的擾動或帶有GARCH誤差的模型,即AR(n)-GARCH(p,q)。
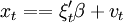 ,
,
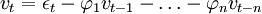 ,
,
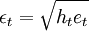
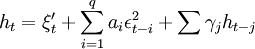 (8)
(8)
三、預測分析與結論
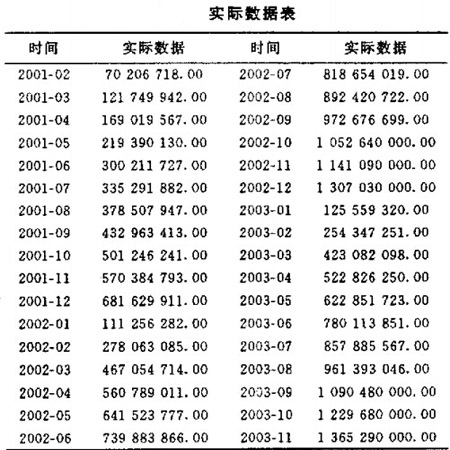
在具體應用時,可在使用模型前依據數據特征對數據進行一些變換,如Log,Logistic,Cox—Box等變換。實際數據如表所示,數據是年內累計的。
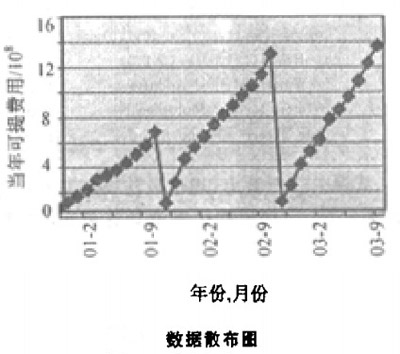
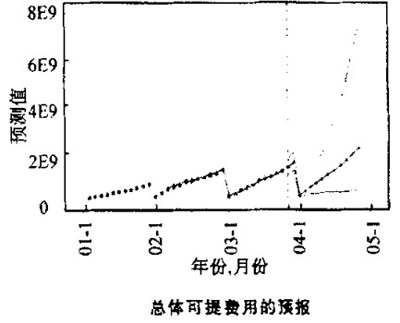
其數據散佈圖如圖所示,其中縱軸表示“當年可提費用”,時間從2001-02~2003-11,共計34個月。
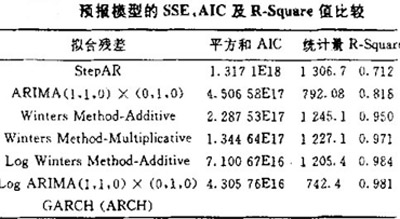
從圖中可以看出,該序列具有明顯的趨勢性和季節性(周期).在具體應用時.可在使用模型之前依據數據特征對數據進行一些變換,如Log,Logistic,Cox-Box等變換.得到各個模型擬合的殘差平方和統計量、R-Square統計量和AIC統計量。如下表所示。
其中GARCH模型SAS系統採用極大似然方法.由於隨機誤差的方差太大,極大似然不能被執行,GARCH模型不能被建立.綜合考慮模型{斂合的殘差平方和統計量、R-Square統計量和AIC統計量,可以看出在各個預報模型中穩健的方法為Log ARIMA(1,1,0)×(O,1,O),因此選擇Log ARIMA(1,l,0)×(O,1.o)預報模型,具體應用過程中,在模擬ARIMA(1,1,0)×(O,l,0)模型之前對數據進行Log變換,即yt=ln(xt)。那麼總體可提費用的數據序列{xt}t=1,2,…,N,N=34)由Log ARIMA(1,1.0)X(0.1,0)預報模型進行預測所產生的參數估計如下表
從而,對數據Log變換後擬合參數的模型為
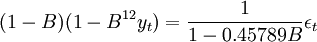 (9)
(9)
其中得到的對未來12個月的預報值段95%置信限(下表)和預報圖及95%置信限圖(下圖),歷史數據(2001-02~2003-11)包括在用於預報圖所給範圍的圖形里,在預報周期的開始位置有一條參考線。
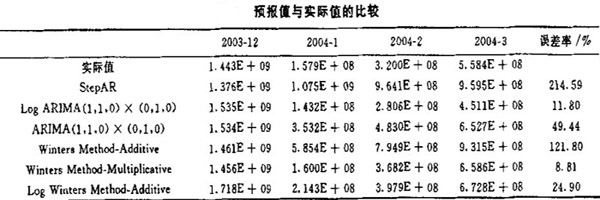
然後,利用得到的外推預報值{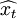 (l)},將其與實際值相比較,得到實際精度.將各個模型得到的003-12,2004-01,2004-02,2004-03預測值與實數據比較的誤差分析結果如上表所示。
(l)},將其與實際值相比較,得到實際精度.將各個模型得到的003-12,2004-01,2004-02,2004-03預測值與實數據比較的誤差分析結果如上表所示。
從誤差分析看出,理論最佳模型具有次優的實際預測誤差,而理論次優模型具有最優的實際預測誤差。
某一城市從1984年到1994年中,每年參加體育鍛煉的入口數,排列起來,共有10個數據構成一個時間序列。我們希望用某個數學模型,根據這10個歷史數據,來預測1995年或以後若幹年中每年的體育鍛煉人數是多少,以便於該城市領導人制訂一個有關體育健身的發展戰略或整個工作計劃。不同的時間序列有不同的特征,例如一個人在一年中每天消耗的糧食基本上是相同的,把這365個數字排列起來。發現它所構成的時間序列總保持在一定水平,上下相差不太大,我們稱它是"平穩"時間序列。它的取值和具體是哪個時期無關,只和時期的長短有關。一般來說.只有屬於平穩過程的時間序列.才是可以被預測的。









非常不錯