季節變動預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
季節變動預測法又稱季節周期法、季節指數法、季節變動趨勢預測法,季節變動預測法是對包含季節波動的時間序列進行預測的方法。要研究這種預測方法,首先要研究時間序列的變動規律。
季節變動是指價格由於自然條件、生產條件和生活習慣等因素的影響,隨著季節的轉變而呈現的周期性變動。這種周期通常為1年。季節變動的特點是有規律性的,每年重覆出現,其表現為逐年同月(或季)有相同的變化方向和大致相同的變化幅度。
首先,利用統計方法計算出預測目標的季節指數,以測定季節變動的規律性;
然後,在已知季節的平均值的條件下,預測未來某個月(季)的預測值。
季節變動的衡量指標主要有:反映季節變動規律的季節變動衡量指標有季節指數、季節比重和季節變差等。
季節指數的計算公式為:
季節指數(%)= (歷年同季平均數/趨勢值)*100%
應當說明的是,這裡的趨勢值有兩種:一是水平趨勢,二是斜坡趨勢。
1.收集歷年(通常至少有三年)各月或各季的統計資料(觀察值)。
2.求出各年同月或同季觀察值的平均數(用A表示)。
3.求出歷年間所有月份或季度的平均值(用B表示)。
4.計算各月或各季度的季節指數,即S=A/B。
5.根據未來年度的全年趨勢預測值,求出各月或各季度的平均趨勢預測值,然後乘以相應季節指數,即得出未來年度內各月和各季度包含季節變動的預測值。
例:根據某市文化衫1996-1998銷售資料預測1999各個季節的銷售量
設:1999年的銷售量以1998年銷售量為基數按8%遞增。
1 2 3 4 5 6 7 季度 1996年 1997年 1998年 各季平均
A=[(2)+(3)+(4)]/3S=A/B Y = Yt*S Ⅰ季度 182 231 330 247 28.9 298.15 Ⅱ季度 1728 1705 1932 1788.3 208.9 2155.16 Ⅲ季度 1144 1208 1427 1259.7 147.2 1518.62 Ⅳ季度 118 134 132 128 15 154.75 合計 3172 3278 3821 3423.7 Y = 1031.67 歷年季度總平均數B=(A1+A2+A3+A4)/4 855.925
案例一:季節變動預測法在醫院管理中的應用[1]
季節變動指在一年內某些經濟現象(一定的時間序列)隨著季節變動而產生波動,它基本上是受自然因素的影響。季節性因素為純粹的時間因素,如氣候、日曆天數和節假日等。本文運用季節變動預測法對醫院診療人次、住院人次這兩項醫院統計的核心指標進行分析預測。
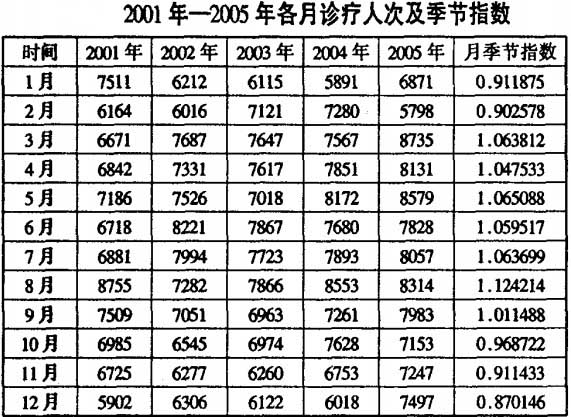
1.診療人次季節變動的測定由表可見,我院診療人次高峰為8月,其次為5月,7月,6月。診療人次最低谷為12月其次為2月和11月。
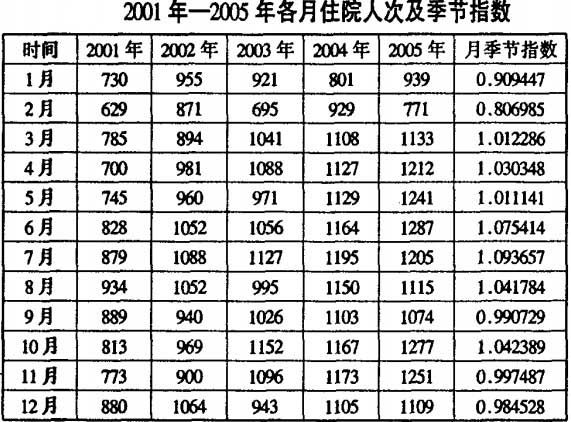
2.住院人次季節變動的測定由表2可見:我院住院人次最高峰為7月,其次為6月,lO月,8月。住院人次最低谷為月,其次為1月和12月。
3.診療人次與住院人次季節指數對照由圖l可見,6月,7月,8月為我院工作高峰期,1月,2月,12月為我院工作低谷3月,5月是門診高峰期病房持平期,10月比較特殊是門診低谷期卻是病房高峰期,11月也是門診低谷期,其餘各月持。
我院診療人次和住院人次主要受長期趨勢和季節變動的影響。運用季節變動預測各月診療人次和出院人次的結果表明:觀察值與預測值基本反映了季節變動規律。病種發作的季節性,農業活動的季節性,農民收入的季節性等都決定了醫院工作的季節性。
變動分析,針對住院人次及診療人次的季節變動特點,院應在醫院工作量的低谷期和持平期安排工作人員休假,業進修,短期業務培訓學習,對設備進行保養。高峰期儘量減人員外出和休假,保證有充足的人員在崗在位;配備必要的藥器材,保證醫葯耗材的供應,合理庫存並降低消耗支,在充分提高醫院社會效益的基礎上提高經濟效益。
案例二:季節指數法在裝備維修用備件預測中的應用[2]
一、季節指數法預測思路
季節指數法是一種時間序列預測技術,來源於經濟活動中銷售量的預測。它是以市場的迴圈周期為特征,通過計算曆史銷售量變化的季節性繫數達到預測目的的一種方法。隨著預測模型的不斷完善,季節指數法已經不局限於經濟預測,它還廣泛應用於預測對象的行為表現為明顯周期波動的社會、科學、技術和軍事等活動。
使用季節指數法預測維修備件消耗量時,須作如下假設:
1.所預測備件的裝備總數量保持不變;差距在允許範圍內,但為了消除累積誤差,應該對模型進行修正。
2.裝備故障率變化呈現近似線性規律,而非急劇變化趨勢;3.備件管理水平未發生重大變革;4.備件的儲備地點和消耗單位恆定。
季節指數法的基本思路是:先分離出不含季節周期波動的長期趨勢;再計算季節指數;最後建立預測模型。數學模型為長期趨勢模式與季節指數之乘積。
假定有一時間序列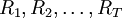 ,T是序列長度,它由N年的統計數據構成。一年季節周期的分段數為K,則有N×K=T,對維修用備件預測的計算過程可以分為以下幾個步驟
,T是序列長度,它由N年的統計數據構成。一年季節周期的分段數為K,則有N×K=T,對維修用備件預測的計算過程可以分為以下幾個步驟
第1步,應用式(1)求K=12(月)或K=4(季)的移動平均值,再對原始數據進行修正。移動平均值公式為
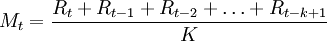 (1)
(1)
式中:t=K,K+1,\ldots,T。
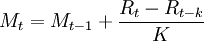 (2)
(2)
式(1)或式(2)是一種簡單移動平均法,預測精度不高,容易產生預測偏差和滯後。但使用簡單移動平均法對原始數據進行預處理,可以消除數據中的異常因素或除去數據中的周期變動成分。移動平均值的下標序號往往和每次平均中所包含的中間一個數據的序號相對應,而通過簡單移動平均法所要修正的也正是中間的那個數據。
根據式(1),當K為偶數,分別對應修正第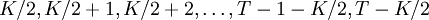 ,即
,即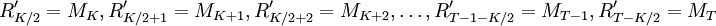 。
。
當K為奇數,分別對應修正第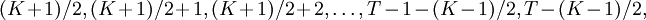 即
即 。
。
第2步,在數據修正的基礎上,計算中心化移動平均值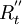 ,然後計算每個周期的季節指數
,然後計算每個周期的季節指數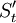 。
。
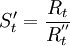 (3)
(3)
式中:t從第1個中心化移動平均值開始。
第3步,計算平均季節指數。
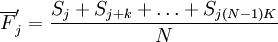 (4)
(4)
式中: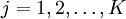 。
。
第4步,對平均季節指數作正規化處理,使其之和等於K,即計算
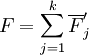 (5)
(5)
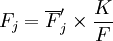 (6)
(6)
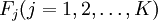 即為最終所求的季節指數。
即為最終所求的季節指數。
第5步,根據長期趨勢和季節指數,建立季節指數法的預測數學模型,當長期趨勢呈線性,預測模型為。
Rt + L = (at + btL)Fj (7)
式中:Rt + L為預測值;t為預測模型所處的時間周期;L為預測期距離預測模型的間隔周期,即到最後一個中心移動平均值的距離;Fj為預測時間所在季節的季節指數;at為觀察期最後一個中心化移動平均值;bt為以觀察期最後2個中心化移動平均值為基礎的變動趨勢值。
二、季節周期預測模型的自適應調整
依據上面的思路求得季節周期預測模型後,可以利用不時得到的新數據對原模型的參數進行校正,不斷提高模型的白適應能力。溫特斯在指數平滑的基礎上,給出了一種自適應校正的計算方法。該方法有3個平滑方程式,分別對長期趨勢(at)、趨勢增量(bt)、季節變動(F_j)作指數平滑,然後,把3個平滑結果用一個預測公式結合起來進行外推預測。
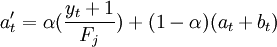 (8)
(8)
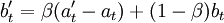 (9)
(9)
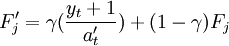 (10)
(10)
式中:\alpha、\beta、\gamma為平滑指數,取值可以相同,也可不同。確定它們的原則是使預測值與實際值之間的均方差為最小。尋求\alpha、\beta、\gamma最恰當的方法是逐步逼近法,一般需要藉助電腦來完成,也可依據經驗選定,一般來說,取值範圍以0.01~O.3為宜。
式(8)中,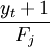 的目的在於消除預測值中的季節性影響,使
的目的在於消除預測值中的季節性影響,使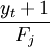 中只含長期趨勢與不規則變動。
中只含長期趨勢與不規則變動。
在理論上,這裡應該用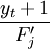 ,但在計算這一步時,式(10)中的F^\prime_j尚未求出,故只好藉助E。按照一次指數平滑原理,式(8)中的(1 − α)後只需at就可以了,但這樣處理會產生滯後偏差。因此,在at,後面添上一個bt,這是為剋服滯後偏差而採取的一項措施。
,但在計算這一步時,式(10)中的F^\prime_j尚未求出,故只好藉助E。按照一次指數平滑原理,式(8)中的(1 − α)後只需at就可以了,但這樣處理會產生滯後偏差。因此,在at,後面添上一個bt,這是為剋服滯後偏差而採取的一項措施。
式(9)中對趨勢的增量作指數平滑,用以表示線性趨勢的增量。式(10)中,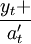 消除了趨勢因素,而只含有季節變動和不規則變動,與上一周期的季節指數F_j聯繫起來作季節指數平滑,以消除不規則變動的影響,反映季節變動。
消除了趨勢因素,而只含有季節變動和不規則變動,與上一周期的季節指數F_j聯繫起來作季節指數平滑,以消除不規則變動的影響,反映季節變動。
在式(8)~式(10)平滑方程的基礎上,可修正算出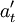 、
、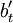 、
、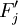 ,然後再利用式(7),就可以計算出下一期的預測值。
,然後再利用式(7),就可以計算出下一期的預測值。
三、預測實例
1.預測對象特點
導航裝備的使用時間服從於飛行訓練,有明顯的時間特性。大部分導航裝備屬於電子設備,受氣候影響明顯,它的故障發生具有季節特征。
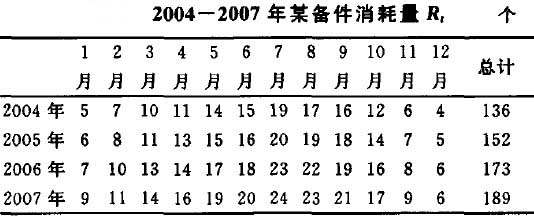
由於技術、體制等方面的原因,某些備件國內無法生產,需要從國外進口,備件供應限制較多,這對備件預測提出了很高的要求。以引進自國外的某近程導航裝備為例,自服役以來,備件供應壓力一直較大。儲備過量,器材失效率增大,且儲備費用也較高;儲備不足,嚴重影響維修工作,減弱導航保障能力。該裝備修複性維修任務由某維修中心承擔,所有備件的請領須通過該中心,維修中心的數據可以客觀準確地反映備件消耗量。
表1是近4年該導航裝備某種備件的消耗詳情。從表中的數據可以看出,備件消耗量具有明顯的季節波動性。因此,可採用季節指數法預測某導航裝備維修備件消耗量。為了提高預測的精度,本文先利用2004-2006年備件消耗數建立預測模型,然後根據2007年實際消耗量來修正模型參數,建立新的預測模型,採用修正後模型預測2008年備件消耗量。
2.移動平均值
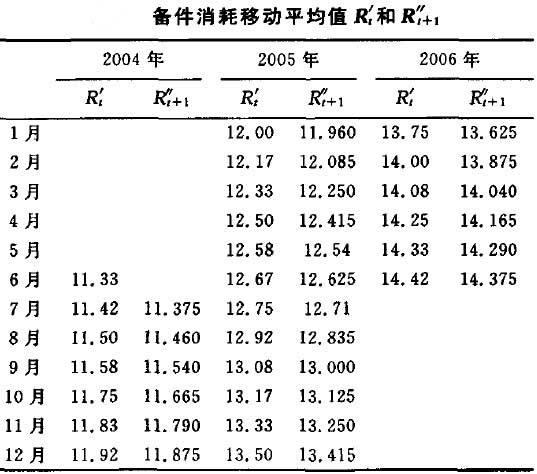
由於備件消耗量在12個月都有波動性,所以取跨越期為12個月,利用式(1)或式(2)計算移動平均值,然後按照步驟一的修正規則,得到修正值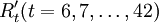 。為了消除季節性變動和不規則變動的影響,需要求得中心化移動平均值
。為了消除季節性變動和不規則變動的影響,需要求得中心化移動平均值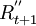 。
。
(t=6,7,\ldots,41),它是利用相鄰的2個平均數加以平均,即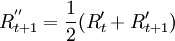 。
。
R^{}_{t+1}包含了長期趨勢,很好地過濾掉季節波動,保持序列基本趨勢,R^\prime_t和R^{}_{t+1}見下表。
3.季節指數利用式(3)、式(4)計算出各年該月的平均季節指數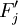 。理想情況下,12個月平均指數之和應該為12,而計算結果為11.992 4,需進行調整,計算出Fj,其結果如表所示。
。理想情況下,12個月平均指數之和應該為12,而計算結果為11.992 4,需進行調整,計算出Fj,其結果如表所示。
4.模型自適應調整
根據表2,建立預測模型為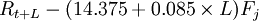 ,,計算得到2007年備件消耗量為185個,而實際消耗量為189個,相差4個,雖然差距在允許範圍內,但為了消除累積誤差,應該對模型進行修正。
,,計算得到2007年備件消耗量為185個,而實際消耗量為189個,相差4個,雖然差距在允許範圍內,但為了消除累積誤差,應該對模型進行修正。
依據式(8)~式(10),運用逐步逼近法,取\alpha=\beta=\gamma=0.2,依次利用下表中2007年各月備件消耗量和上表中季節指數,對數據按月逐次校正,最後得到: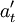 ,
,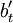 ,調整後的季節指數如下表。
,調整後的季節指數如下表。
調整後的季節指數Fj
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | 總數 | |
| 指數 | 0.5137 | 0.6842 | 0.8977 | 1.0072 | 1.1839 | 1.2503 | 1.6290 | 1.4972 | 1.3898 | 1.0607 | 0.5285 | 0.3578 | 12.0000 |
5.利用模型預測
建立新預測模型為
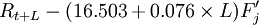
消耗量,如下表。當預測年度備件消耗時,使用下表“年消耗”預測值,年度總消耗為21l(個),而如果以月為採購單元時,採用下表“月消耗”預測由此模型和上表,可以預測2008年該備件的值,每月消耗情況分別可以得到。
2008某備件消耗預測表
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 | 總計 | |
| 年消耗 | 8.73 | 11.64 | 15.32 | 17.25 | 20.35 | 21.28 | 27.63 | 25.64 | 24.05 | 18.51 | 9.31 | 6.38 | |
| 月消耗 | 10 | 12 | 16 | 18 | 21 | 22 | 29 | 27 | 25 | 19 | 10 | 7 | 216 |
若用GM(1,1)預測[3],得2008年備件消耗量為209,預測精度為一級。季節指數法預測結果與GM(1,1)預測相差不到1%,說明預測精度較高。
採用的預測方法,可充分利用維修一線的詳細數據,預測下一時間段每月的備件消耗情況,為備件供給部門合理採購、儲存備件提供了可靠的依據。模型經過每個周期不斷的自適應調整後,預測誤差很小,完全符合預測要求。該方法能較客觀地預測裝備維修用備件的消耗量,但需要一定的假設條件,且僅適用於1~3年的短期預測。
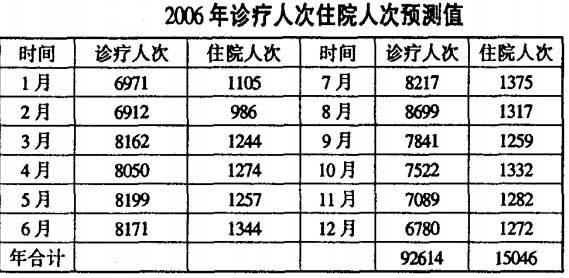









醫療的案例,沒看明白2006年各類病人數量如何預測出來的?前面都只是描述了季節變化趨勢,未描述如何根據季節變化趨勢預測下一年情況