直線修勻法

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是直線修勻法^[1]

　　直線修勻法是動態數列修勻法的一種。按直線來修勻動態數列，用以確定最接近實際數列的理論數列的方法。

直線修勻法的應用^[1]

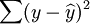　　把原始數列修勻成一條直線的方法很多。一般認為用最小二乘法得出的直線是“最佳”直線。用最小二乘法求得的趨勢直線能使原數列實際數值(y)與趨勢直線上相對應的理論數值 $(\widehat{y})$ 的窩差平方和為最小，即 $\sum(y-\widehat{y})^2$ 為最小。趨勢直線方程式為： $\widehat{y}=a+bx$ ……1為了求得上式的參數a和b，可利用以下兩個標準方程式：

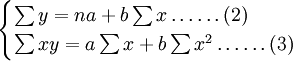
　　 $\begin{cases}\sum y=na+b\sum x\ldots\ldots(2)\\\sum xy=a\sum x+b\sum x^2\ldots\ldots(3)\end{cases}$

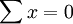　　使 $\sum x=0$ ,則簡化為：

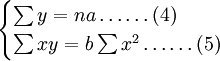
　　 $\begin{cases}\sum y=na\ldots\ldots(4)\\\sum xy=b\sum x^2\ldots\ldots(5)\end{cases}$

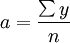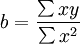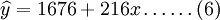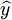　　用下表資料來說明理論數列的計算過程。按表列資料代入公式解方程求出 $a=\frac{\sum y}{n}$ 為1676； $b=\frac{\sum xy}{\sum x^2}$ 為216再代入(1)式趨勢直線方程式為: $\widehat{y}=1676+216x\ldots\ldots(6)$ 將上表 $\widehat{y}$ 欄數字分別代入(6)，即為 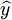$\widehat{y}$ 欄各年的理論數字

年份	產量(萬公斤)	年份(第三年為中央年的離中差)	產量與年份乘積	產量理論數
n	y	x	xy	$x 2$	$\widehat{y}=a+bx$
第一年	1301	-2	-2602	4	1244
第二年	1435	-1	-1435	1	1460
第三年	1611	0	0	0	1676
第四年	1869	1	1869	1	1892
第五年2164	2	4328	4	2108
n=5	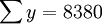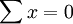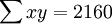$\sum y=8380$	$\sum x=0$	$\sum xy=2160$	$\sum x^2=10$	8330