干預分析模型預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
干預分析模型(Intervention analysis model)
目錄 |
①干預的含義：時間序列經常會受到特殊事件及態勢的影響，稱這類外部事件為干預。是指預測模型擬合的好壞程度，即由預測模型所產生的模擬值與 歷史實際值擬合程度的優劣。
②研究干預分析的目的：從定量分析的角度來評估政策干預或突發事件對經濟環境和經濟過程的具體影響。
干預分析模型的基本變數是干預變數，有兩種常見的干預變數：一種是持續性的干預變數，表示T 時刻發生以後, 一直有影響，這時可以用階躍函數表示，形式是：
第二種是短暫性的干預變數，表示在某時刻發生, 僅對該時刻有影響, 用單位脈衝函數表示，形式是：
干預事件雖然多種多樣，但按其影響的形式，歸納起來基本上有四種類型：
- a. 干預事件的影響突然開始，長期持續下去，設干預對因變數的影響是固定的，從某一時刻T開始，但影響的程度是未知的，即因變數的大小是未知的。
這種影響的干預模型可寫為
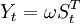
表示干預影響強度的未知參數。 不平穩時可以通過差分化為平穩序列，則干預模型可調整為
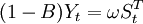
其中B為後移運算元。如果干預事件要滯後若幹個時期才產生影響，如b個時期，那麼干預模型可進一步調整為
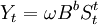
- b. 干預事件的影響逐漸開始，長期持續下去有時候干預事件突然發生，並不能立刻產生完全的影響，而是隨著時間的推移，逐漸地感到這種影響的存在。
這種形式的最簡單情形的模型方程為
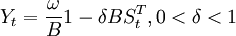
更一般的模型是：
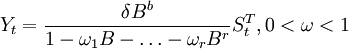
- c. 干預事件突然開始產生暫時的影響，這類干預現象可以用數學模型描述如下：
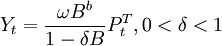
當δ = 0時，干預的影響只存在一個時期，當δ = 1時，干預的影響將長期存在。
- d. 干預事件逐漸開始產生暫時的影響
干預的影響逐漸增加，在某個時刻到達高峰，然後又逐漸減弱以至消失。這類干預現象可用以下模型去描繪：
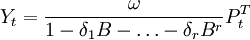
- （1）干預模型的構造與干預效應的識別
單變數時間序列的干預模型，就是在時間序列模型中加進各種干預變數的影響。設平穩化後的單變數序列滿足下述模型：
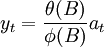
又設干預事件的影響為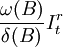
，其中
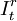為干預變數，它等於
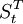或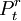
，則單變數序列的干預模型為
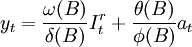
這裡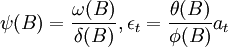
在此模型基礎上要根據序列變化的現實資料，對ψ(B)與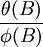
進行識別。
干預模型建模的思路和具體步驟為：
a.利用干預影響產生前的數據，建立一個單變數的時間序列模型。然後利用此模型進行外推預測，得到的預測值，作為不受干預影響的數值。最後將實際值減去預測值，得到的是受干預影響的具體結果，利用這些結果可以求估干預模型的參數。
b.估計出干預模型的參數。
c.利用排除干預影響後的全部數據，識別與估計出一個單變數的時間序列模型。
d.求出總的干預分析模型。
案例一:中國鋼鐵產品市場價格干預分析模型研究[1]
一、引言
鋼鐵產品市場價格的變化受多種因素的影響，這種影響是隨機的均衡的。但現實生活中這些因素有時是突變的，對鋼材市場造成衝擊和干預，尤其是巨集觀經濟政策、政治自然等因素。如何將這種影響的幅度和持續性定量地描述出來，對於深入認識我國鋼材市場的波動特征是非常有意義的。
二、巨集觀調控及對鋼材市場的影響
2005年中國鋼材市場在大起大落中走過了極不平靜的一年。自2004年12月中旬國內鋼材市場開始呈現出“淡季不淡”，價格“逆市”上揚的運行態勢後，在2005年初更是藉助鐵礦石進口協議價格大幅上漲“東風”的推動，價格持續大幅走高，使得市場風險明顯走高，加之市場需求的跟進乏力，部分商家信心也開始有所動搖。3月30日溫家寶總理主持召開國務院常務委員會，會議強調要加強對鋼鐵行業、房地產行業的巨集觀調控，此後一系列針對鋼鐵和房地產行業的調控措施陸續出台，從3月下旬起，國內鋼材市場開始進入了漫長的下行通道。
2005年的巨集觀調控明顯具有針對性。2004年國家通過提高央行準備金率、清理固定資產投資項目、清理整頓開發區等方式給所有投資降溫。2005年的目標則定位明確，針對鋼材價格上漲過快的問題，國家集中出台了一系列巨集觀調控措施抑制鋼材價格，這些措施既有針對鋼鐵行業本身的，也有針對下游消費行業的。從2005年4月1日起正式取消鋼坯、鋼錠出口退稅；從2005年5月1日起將2O種鋼材產品的出口退稅率從13％下調至11％；從2005年5月19t3起將鐵礦石、生鐵、廢鋼、鋼坯等產品列入加工貿易禁止類商品目錄，這是對鋼鐵行業本身的調控措施；2005年3月29日，國土資源部提出今年將繼續嚴格土地市場治理整頓，繼續實行從嚴從緊的建設用地供應政策，嚴把土地閘門；國務院辦公廳2005年5月11日轉發建設部等七部委《關於做好穩定住房價格工作的意見》，通知要求要解決房地產投資規模過大、價格上漲幅度過快等問題，這是對鋼材消費行業採取的調控措施。
這些政策傳遞了中央通過控制需求，進而控制重要生產資料價格過快上漲的決心。這一系列措施抑制了鋼材需求增長，導致鋼材庫存增加，企業流動資金困難，引發了包括板材在內的國內鋼材市場價格大幅下滑。巨集觀調控對人的心理預期很大，鋼鐵企業、下游廠商和經銷商普遍預期鋼材價格下跌，導致推遲電貨，這就肯定會影響需求。
政府巨集觀調控政策的緊密出台打壓了鋼材市場的中間需求和有效需求的釋放，促使鋼材市場出現下跌。一方面國內的貿易商心態變差，為了緩解緊張的資金壓力及保住市場份額，紛紛降價；另一方面影響了市場有效需求的釋放，儘管國內鋼材市場真實需求依舊相對堅挺，但受消費用戶買漲不買跌心理影響，市場有效需求釋放不足，觀望氣氛濃厚。
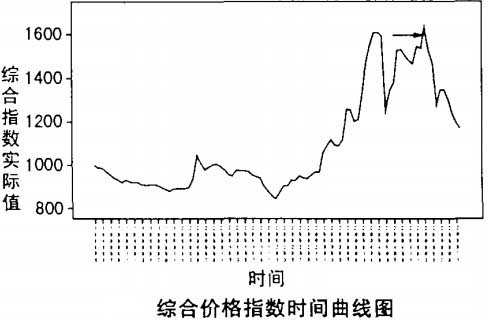
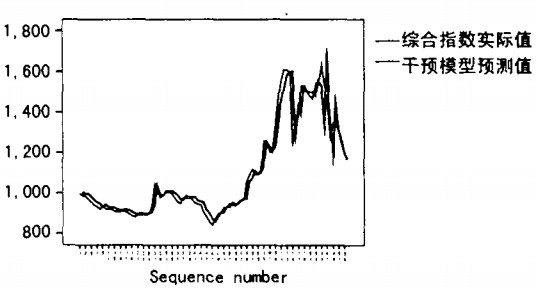
從以上分析可以看出，2005年4月是鋼材市場的一個分水嶺，其中巨集觀經濟政策干預效用明顯。下圖是1998年3月至2005年12月中國鋼材市場綜合價格指數時間曲線圖(採樣頻率一月一次)，箭頭所示為2005年4月市場價格峰值。(見下圖)。
三、干預分析模型的理論
干預分析模型(InterventionAnalysisMode1)是由美國威斯康辛大學的博克斯教授和刁錦寰教授(BoxAndTiao)於2O世紀7O年代提出的一種時間序列分析模型。這種方法始於對美國西海岸洛杉磯大氣污染的環境問題的研究，此後引起眾多經濟學家的重視，被廣泛應用於經濟政策的變化或突發事件(戰爭爆發、罷工、廣告促銷等)給經濟帶來影響的定量分析。在國內，有學者將這種分析方法應用於研究我國農村經濟體制改革的實效、物價波動的干預效用問題，但如何將這種分析方法運用於分析巨集觀經濟政策衝擊對我國鋼鐵產品市場對我國股票市場的影響則還沒有。
干預模型是時間序列分析中傳遞函數模型的一種推廣。在干預模型模型，干預變數是模型的基本變數。所謂干預變數，是代表干預的一種虛擬變數，它作為模型的輸入變數來解釋干預事件對響應變數的影響。常用的干預變數有兩種：一種是一但發生就會產生長期影響的持續干預變數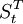；另一種是發生後只有短暫性影響的暫時性干預變數
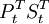可用一個階梯函數來表示：。
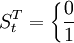
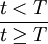
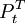可以表示為一個脈衝函數:
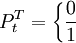
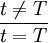
式中T表示乾干預事件發生的時間。上述兩類干預變數雖然表示形式不同，但它們之間有如下的內在聯繫：
。
B為後移運算元。
在現實中，干預事件的影響形式可以有多種形式，但按其影響的特點，可以歸納出如下四種基本類型：
(1)影響突然開始且長期持續下去：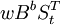
(2)影響緩慢開始，然後長期持續下：
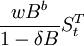。當δ = 0時，干預的影響只存在一個時期；當δ = 1時，干預的影響將長期存在；當0 < δ < 1時，干預的影響以速度漸進衰減，最後回到干預前的水平。
(4)影響緩慢開始，持續時間短暫：
在較複雜的情況時，可以將上面的四種模型都組合起來
一般地，干預模型具有下麵的形式：
。
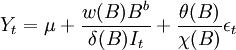其中，B為後移運算元，εt為白雜訊序列，B^b表示干預影響延遲b期才起作用，當b=0，表示干預事件一齣現就立即產生影響。It代表干預變數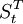或。
模型的待估參數為：
w = (w0,w1,Μ,ws),δ = (δ1,δ2,Μδr),θ = θ1,θ2,Μθq),χ = χ1,χ2,Μχp)。
從中國鋼鐵產品市場價格的實際數據來看，每次巨集觀經濟政策的出台，都會對市場價格產生突然衝擊，然後長期持續下去。因此，這裡選擇如下形式的干預模型：
。
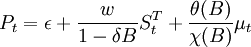二、干預分析模型的識別與參數估計
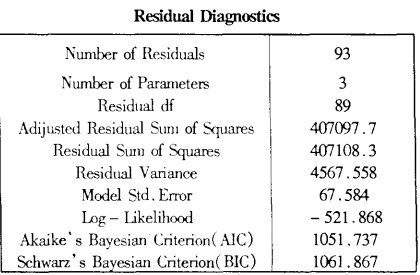
利用干預影響產生前(1998年3月至2005年4月)的數據，即巨集觀調控政策出台前的市場價格數據，建立一個單變數的ARIMA模型(自回歸求積移動平均Austoreg Ressive Integrated MovingAverage縮寫為ARIMA)。然後，利用此模型進行趨勢外推預測，得到的預測值，作為不受干預影響的數值。最後將實際值減去這些預測值，得到的是受干預影響的的具體結果。利用這些結果可以估計干預模型的參數。
(一)建立一個單變數的ARIMA模型
1．數據的處理
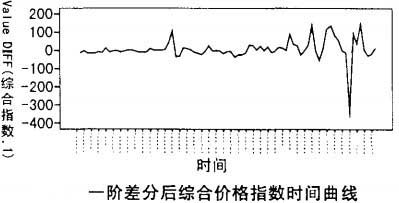
觀察圖1所視綜合價格指數時間曲線，發現數據非平穩含有明顯的趨勢項。對數據進行一階差分，數據即變為平穩隨機序列，如下圖：
2．ARIMA(P，d，q)模型的識別
所謂模型的識別，即根據所要處理的數據序列的統計特征，來確定P、d和q的值。
由前面所述，一階差分後價格綜合指數的趨勢就消除了，因此d=1。
在實際識別ARIMA(p，q)模型時，需多次反覆償試，有可能存在不止一組(p，q)值都能通過識別檢驗。
顯然，增加P與q的階數，可增加擬合優度，但卻同時降低了自由度。
因此，對可能的適當的模型，存在著模型的“簡潔性”與模型的擬合優度的權衡選擇問題。通常，ARMA(p，q)過程的偏自相關函數(PACF)可能在P階滯後前有幾項明顯的尖柱(spikes)，但從P階滯後項開始逐漸趨向於零。而它的自相關函數(ACF)則是在q階滯後前有幾項明顯的尖柱，從q階滯後項開始逐漸趨向於零。
因此，用一階差分後的數據偏相關係數判別P，用自噪音。
相關係數判別q，得出(P，q)的所有可能取值。其中，P由顯著不為零的偏相關係數的數據決定；q由顯著不為零的自相關係數的數據決定。
將綜合價格指數一階差分後的數據輸入SPSS計算ACF-PACF得到優化後的結果：p=3，q=0。
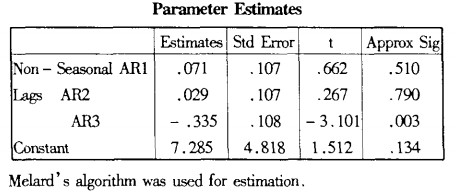
3．ARIMA(P，d，q)的參數識別。
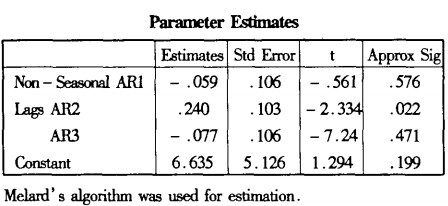
將上面求得的P、d、q和綜合價格指數數據輸入SPSS計算模型參數如下：
。
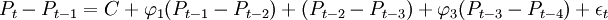移項得：P_t=C(1+\varphi_1)P_{t-1}+(\varphi_2-\varphi_1)P_{t-2}+(\varphi_3-\varphi_2)P_{t-3}-\varphi_3P_{t-4})+\epsilon_t。
將\varphi_1=AR1、\varphi_1=AR2、\varphi_1=AR3代入上式得：P_{t1}=7.285+1.071P_{t-1}-0.042P_{t-2}-0.364P_{t-3}+0.335P_{t-4}+\epsilon_t。
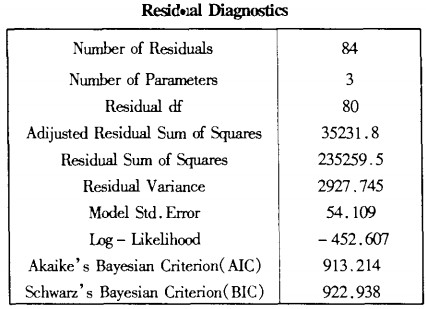
4．ARIMA(P，d，q)的模型檢驗由於ARIMA(P，d，q)模型的識別與估計是在假設隨機擾動項是白雜訊的基礎上進行的，因此，如果估計的模型確認正確的話，殘差εt應代表一白雜訊序列。
如果通過所估計的模型計算的樣本殘差不代表一白雜訊，則說明模型的識別與估計有誤，需重新識別與估計。
在實際檢驗時，主要檢驗殘差序列是否存在自相關
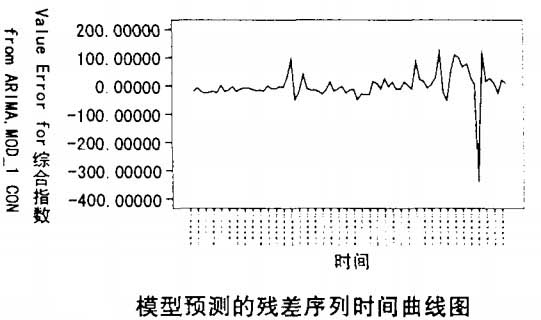
將上述A腳MA(3,1,0)得到的預測值與實際值的殘差序列求算術平均值為-0.1761752，基本接近零均值。
殘差序列時間線圖如下，沒有趨勢項，類似隨機白噪音
(二)建立干預分析模型
1．干預模型參數的估計
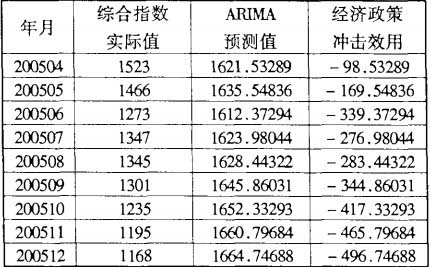
運用ARIMA(3,1,0)模型對2005年4月到12月的市場價格數據進行外推預測，然後用實際值減去預測值，得到的差值就是巨集觀調控政策所產生的衝擊效用，記為Zt。
利用上表數據可以估計處干預模型的參數：
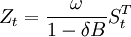
其中，當t<86時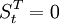
，當t≥86時
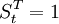。參數估計如下：
ω = − 307.057,δ = 0.873。
2．計算凈化序列並建立新的ARIMA模型
凈化序列是指消除了干預影響的序列，它由實際的觀察值序列減去干預影響值得到：
。
Pt為消去了干預影響的凈化序列。同樣對凈化序列求ARNA(3，1，0)模型如下：
Pt2 = 6.635 + 0.041Pt − 1 − 0.181Pt − 2 + 0.163Pt − 3 + 0.077Pt − 4 + εt
3.組建干預分析模型
。
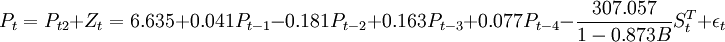其中，當t<86(2005年4月)時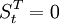，當t≥86時(2005年4月)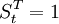
(4)干預分析模型的檢驗
平均絕對差：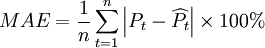
。
平均絕對差率：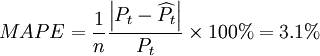
。
均方根誤差：![RMSE=\sqrt{\frac{1}{n}\sum_{t=1}^n[P_t-\widehat{P_t}]^2}=65.76](/w/images/math/8/6/3/863e85d83b9eceb33192b9d6115bd7d4.png)
。
模型擬合度：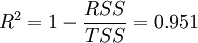
鋼鐵產品市場是生產資料市場，其價格的變化除了受供求關係等市場規律的影響，還直接受到國家巨集觀經濟政策的外在衝擊(最終也表現為供求的影響)。干預模型是定量分析巨集觀經濟政策影響對鋼鐵產品市場衝擊效用的有效手段之一。
- ↑ 謝向前.中國鋼鐵產品市場價格干預分析模型研究[J].武漢冶金管理學院學報.2006(3)
評論(共8條)
你好，不好意思那麼冒昧的打擾你，我是一名學生，看到你的博客里關於干涉預測模型的解算方法，我這一個多月都在研究這個演算法，但是遇到了很大的困難，想咨詢一下你關於這個演算法裡面的參數要怎麼解算？想問下怎麼方面能和你直接聯繫你，十分感謝了
你學過計量嗎？學過的話，這些數據都是利用回歸，最小二乘法在Eviews里運行得出
你好，我做畢業論文也需要用到干預分析模型，不明白ω = − 307.057,δ = 0.873是怎麼估計出來的，真心向您請教
模型Z_t=ω/(1-δB) S_t^T中，S_t^T=1,因此相當於估計Z_t=ω/(1-δB)即（1-δB）*Z_t=ω，即Z_t-δB*Z_t=ω，即Z_t=δB*Z_t+ω，即Z_t=δZ_(t-1)+ω，相當於做一個AR(1)模型，用最大似然估計，就可得到上述得數
你好我使用AR(1)擬合的干預模型是斜向下的直線，但是我的干預值呈現V字形，感覺很不對，是哪裡出現問題了嗎
你好，我做畢業論文也需要用到干預分析模型，不明白ω = − 307.057,δ = 0.873是怎麼估計出來的，真心向您請教
加一
你好，不好意思那麼冒昧的打擾你，我是一名學生，看到你的博客里關於干涉預測模型的解算方法，我這一個多月都在研究這個演算法，但是遇到了很大的困難，想咨詢一下你關於這個演算法裡面的參數要怎麼解算？想問下怎麼方面能和你直接聯繫你，十分感謝了