投资组合管理

出自 MBA智库百科(https://wiki.mbalib.com/)

　　投资组合管理是指投资管理人按照资产选择理论与投资组合理论对资产进行多元化管理，以实现分散风险、提高效率的投资目的。

　　基金经理一方面可以通过组合投资的方法来减少系统风险，另一方面可以通过各种风险管理措施来对基金投资的系统风险进行对冲，从而有效降低投资风险。而中小投资者由于资金量和 专业知识方面的欠缺，很难做到组合投资。因此，从这一点来说，基金非常适合平时工作繁忙，又不具备相关金融投资知识的中小投资者进行家庭理财。

　　在设计投资组合时，基金管理人一般依据下列原则：

　　在风险一定的条件下，保证组合收益的最大化；

　　在一定的收益条件下，保证组合风险的最小化。

　　具体来说，需要考虑以下几个方面的问题：

　　第一，进行证券品种的选择，即进行微观预测，也就是进行证券投资分析，主要是预测证券的价格走势以及波动情况。

　　第二，进行投资时机的选择，即宏观预测，预测和比较各种不同类型的证券的价格走势和波动情况。例如，预测普通股相对于公司债券等固定收益证券的价格波动。

　　第三，多元化，即依据一定的现实条件，组建一个风险最小的资产组合。

　　1、传统投资组合的思想——Native Diversification

　　（1）不要把所有的鸡蛋都放在一个篮子里面，否则“倾巢无完卵”。

　　（2）组合中资产数量越多，分散风险越大。

　　2、现代投资组合的思想——Optimal Portfolio

　　（1）最优投资比例：组合的风险与组合中资产的收益之间的关系有关。在一定条件下，存一组在使得组合风险最小的投资比例。

　　（2）最优组合规模：随着组合中资产种数增加，组合的风险下降，

　　但是组合管理的成本提高。当组合中资产的种数达到一定数量后，风险无法继续下降。

　　现代投资理论的产生与发展

　　现代投资组合理论主要由投资组合理论、资本资产定价模型、APT模型、有效市场理论以及行为金融理论等部分组成。它们的发展极大地改变了过去主要依赖基本分析的传统投资管理实践，使现代投资管理日益朝着系统化、科学化、组合化的方向发展。

　　1952年3月，美国经济学哈里·马考威茨发表了《证券组合选择》的论文，作为现代证券组合管理理论的开端。马考威茨对风险和收益进行了量化，建立的是均值方差模型，提出了确定最佳资产组合的基本模型。由于这一方法要求计算所有资产的协方差矩阵，严重制约了其在实践中的应用。

　　1963年，威廉·夏普提出了可以对协方差矩阵加以简化估计的夏普单因素模型，极大地推动了投资组合理论的实际应用。

　　20世纪60年代，夏普、林特和莫森分别于1964、1965和1966年提出了资本资产定价模型（CAPM）。该模型不仅提供了评价收益一风险相互转换特征的可运作框架，也为投资组合分析、基金绩效评价提供了重要的理论基础。

　　1976年，针对CAPM模型所存在的不可检验性的缺陷，罗斯提出了一种替代性的资本资产定价模型，即APT模型。该模型直接导致了多指数投资组合分析方法在投资实践上的广泛应用。

　　投资组合(Portfolio)管理的目的是：

　　按照投资者的需求，选择各种各样的证券和其他资产组成投资组合，然后管理这些投资组合，以实现投资的目标。投资者需求往往是根据风险（Risk）来定义的，而投资组合管理者的任务则是在承担一定风险的条件下，使投资回报率（return）实现最大化。

　　投资组合管理由以下三类主要活动构成：

　　（1）资产配置

　　（2）在主要资产类型间调整权重

　　（3）在各资产类型内选择证券。

　　资产配置的特征是把各种主要资产类型混合在一起，以便在风险最低的条件下，使投资获得最高的长期回报。投资组合管理者以长期投资目标为出发点，为提高回报率时常审时度势改变各主要资产类别的权重。例如，若一个经理判断在未来年份内权益的总体状况要比债券的总体状况对投资者更加有利的话,则极可能要求把投资组合的权重由债券向权益转移，而且，在同一资产类型中选择那些回报率高于平均回报率的证券，经理便能改善投资组合回报的前景。

　　投资组合的构建就是选择纳入投资组合的证券并确定其适当的权重，即各证券所占该投资组合的比例。马考维茨（Markowitz）模型表明，构建投资组合的合理目标应是在给定的风险水平下形成一个具有最高回报率的投资组合。具有这种特征的投资组合叫做有效的投资组合，它已经被广泛地接受为最优投资组合构建的典范。

　　此外，马考维茨模型还为构建能实现最有效这一目标的投资组合提供了一种明确的和修炼的过程（这种过程被称为最优化），这种最优化过程已经被广泛地应用于大型计划的投资者确定投资组合中各主要资产类型的最佳组合的活动中。这种过程通常被称做资产配置（asset allocation），因为实际中可考虑的主要资产类型是有限的，所以它是可操作的。当考虑的证券总体数目超过某一限制时，马考维茨最优化过程是难以实践的，因此就需要采用将在下两章讨论的其他替代方法。

　　由于马考维茨模型提出了有效投资组合构建中的基本概念，也为投资组合分析的其他方面奠定了基础。其中将涉及有效的投资组合和多样化的概念，这些概念是构建投资组合的基础。

　　投资组合的构建过程是由下述步骤组成：

　　首先，需要界定适合于选择的证券范围。对于大多数计划投资者其注意的焦点集中在普通股票、债券和货币市场工具这些主要资产类型上。近来，这些投资者已经把诸如国际股票、非美元债券也列入了备选的资产类型，使得投资具有全球性质。有些投资者把房地产和风险资本也吸纳进去，进一步拓宽投资的范围。虽然资产类型的数目仍是有限的，但每一资产类型中的证券数目可能是相当巨大的。

　　其次，投资者还需要求出各个证券和资产类型的潜在回报率的期望值及其承担的风险。此外，更重要的是要对这种估计予以明确地说明，以便比较众多的证券以及资产类型之间哪些更具吸引力。进行投资所形成投资组合的价值很大程度上取决于这些所选证券的质量。

　　构建过程的第三阶段，即实际的最优化，必须包括各种证券的选择和投资组合内各证券权重的确定。在把各种证券集合到一起形成所要求的组合的过程中，不仅有必要考虑每一证券的风险－回报率特性，而且还要估计到这些证券随着时间的推移可能产生的相互作用。马考维茨模型用客观和修炼的方式为确定最优投资组合提供了概念性框架和分析方法。

　　管理投资组合是一个持续的过程，同时涵盖了对静态资产和动态资产（比如项目等）的管理。在 实际运行过程中，管理投资组合真正的难点在于它需要时刻保持高度的商业敏感，不断地进行分析和检讨，考察不断出现的新生机会、现有资产的表现以及企业为了利用现有机遇而进行的 资源配置活动等等。

　　在瞬息万变的现实环境中，那些影响投资组合的资产和项目的价值往往都处在一个随时变化波动的状态之下，造成这种波动的原因可能是来自外部的影响因素：包括市场地位变化或者公司本身竞争地位的变化；同样，这种波动也可能是归因于内部的某些力量（比如：公司战略、产品组合、分销渠道的调整或者诸如成本和质量等竞争基础发生变化）。

　　成本角度

　　在投资组合引入阶段，对每一个组件都需要从技术、运营、人力成本等方面着手进行成本分析，预先确定一个可接受 的成本浮动范围。在投资组合运行过程中，投资组合管理就应将各个组件的成本努力控制在这一范围内，同时根据需要及时调整各个组件在组合中的成本比重，以实 现组合整体的成本效益最大化。

　　收益角度

　　在投资组合的实际运行环境下，组合成本结构的调整、组件表现、股东权益、客户及关系、内部流程、组织学习和提升能力等众多因素会对组合产生方方面面的影响，投资组合管理要确保在这些影响下各组件仍然能够保证预计的收益。就“收入”来讲，在投资组合引入阶段，考虑到资金的时间价值，我们往往预期某项收入能够在特定的时间产生，也就是说我们会给某项投资组合预设一个“收益实现轨迹”，而投资组合管理就要保证各个组件 收益获得时间的确定性，也就是要尽量使收益符合这个“收益实现轨迹”。在投资组合整体收益的管理上，我们也有必要把外部市场环境、法律法规、时间、竞争力 等影响组件价值的因素考虑在内。

　　风险管理角度

　　投资组合的组件必须多样化而且要被控制在企业能够承受的风险范围之内。投资组合组件可以按照产出或者风险 划分为几个等级。风险因素需要和达到预期收益的可能性、稳定性、技术风险等结合起来考虑。组件的风险等级决定了对其管理的紧密程度——包括审查的频繁程度以及资本更新的模式。

　　现有资产的投资组合需要从上文提及的各个角度进行管理，这些都是静态的，所以，我们还有必要从一种互动的角度出发来进行管理，也就是说还要仔细考查这些组件之间如何互动，组件和企业如何互动。

　　证券组合管理是一种以实现投资组合整体风险一收益最优化为目标，选择纳入投资组合的证券种类并确定适当权重的活动。它是伴随着现代投资理论的发展而兴起的一种投资管理方式。

　　1．设定投资政策；

　　2．进行证券分析；

　　3．构造投资组合；

　　4．对投资组合的效果加以评价；

　　5．修正投资组合。

　　(一)投资者以期望收益率和方差(或标准差)来评价单个证券或证券组合

　　(二)投资者是不知足的和厌恶风险的

　　(三)投资者的投资为单一投资期

　　(四)投资者总是希望持有有效资产组合

　　投资涉及到现在对未来的决策。因此，在投资上，投资者更多地需要对投资的未来收益率进行预测与估计。马克威茨认为，由于未来收益率往往是不确定的，表现为一个随机变量。因此，可以以期望收益率作为对未来收益率的最佳估计。

　　数学上，单个证券的期望收益率(或称为事前收益率)是对各种可能收益率的概率加权，用公式可表示为：

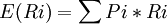
　　其中，Pi表示各种可能收益率的概率；

　　Ri表示各种可能收益率。

　　收益率的概率分布往往是未知的，在这种情况下，一方面可以通过引入主观概率的方式进行期望收益率的计算，另一方面则可以通过样本估计的方式进行期望收益率的计算。

　　假设收益率的概率分布恒定，给定证券的月或年实际收益率用下式估计：

　　其中，R表示样本平均收益率；

　　n表示实际收益率的个数；

　　Rt表示实际收益率的时间序列值；

　　已知收益率的概率分布，可以用方差或标准差衡量证券的风险：

　　方差：δ² = Pi * (Ri − E(Ri))²

　　标准差：

　　标准差越大，说明证券的收益率的波动性越大，风险也就越大。