標準誤差
出自 MBA智库百科(https://wiki.mbalib.com/)
標準誤差(Standard error),也稱均方根誤差(Root mean squared error)
目錄 |
標準誤差是指在抽樣試驗(或重覆的等精度測量)中,常用到樣本平均數的標準差。註意:標準差與標準誤差是兩個不同的概念[1]。
標準誤差是當前應用最廣泛、最基本的一種隨機誤差的表示方法,當標準誤差求得後,平均誤差和極限差即可求得 故國際上普遍採用標準誤差作為實驗結果質量的數字指標,同時按國際計量局建議,不確定度用標準差σ表徵(或方差σ2表徵)。由此可知,標準誤差在數據處理上的作用十分重要[2]。
設n個測量值的誤差為E1、E2……En,則這組測量值的標準差σ等於:
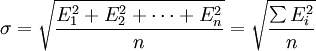
其中,E = Xi − T,式中:E-誤差;Xi-測定值;T-真實值。
由於被測量的真值是未知數,各測量值的誤差也都不知道,因此不能按上式求得標準誤差。測量時能夠得到的是算術平均值,它最接近真值(N),而且也容易算出測量值和算術平均值之差,稱為殘差(記為v)。理論分析表明可以用殘差v表示有限次(n次)觀測中的某一次測量結果的標準差σ,其計算公式為:
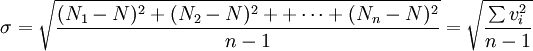
對於一組等精度測量(n次測量)數據的算術平均值,其誤差應該更小些。理論分析表明,它的算術平均值的標準誤差。有的書中或計算器上用符號s表示):
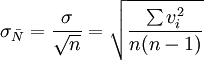
需要註意的是,標準誤差不是測量值的實際誤差,也不是誤差範圍,它只是對一組測量數據可靠性的估計。標準誤差小,測量的可靠性大一些,反之,測量就不大可靠。進一步的分析表明,根據偶然誤差的高斯理論,當一組測量值的標準誤差為σ時,則其中的任何一個測量值的誤差Ei有68.3%的可能性是在(-σ,+σ)區間內。
世界上多數國家的物理實驗和正式的科學實驗報告都是用標準誤差評價數據的,現在稍好一些的計算器都有計算標準誤差的功能,因此,瞭解標準誤差是必要的。
標準誤與標準差的區別[1]
標準差與標準誤的意義、作用和使用範圍均不同。標準差(亦稱單數標準差)一般用s表示,是表示個體間變異大小的指標,反映了整個樣本對樣本平均數的離散程度,是數據精密度的衡量指標;而標準誤一般用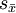 表示,反映樣本平均數對總體平均數的變異程度,從而反映抽樣誤差的大小,是量度結果精密度的指標。
表示,反映樣本平均數對總體平均數的變異程度,從而反映抽樣誤差的大小,是量度結果精密度的指標。
隨著樣本數(或測量次數)n的增大,標準差趨向某個穩定值,即樣本標準差s越接近總體標準差σ,而標準誤則隨著樣本數(或測量次數)n的增大逐漸減小,即樣本平均數越接近總體平均數μ;故在實驗中也經常採用適當增加樣本數(或測量次數)n減小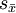 的方法來減小實驗誤差,但樣本數太大意義也不大。標準差是最常用的統計量,一般用於表示一組樣本變數的分散程度;標準誤一般用於統計推斷中,主要包括假設檢驗和參數估計,如樣本平均數的假設檢驗、參數的區間估計與點估計等。
的方法來減小實驗誤差,但樣本數太大意義也不大。標準差是最常用的統計量,一般用於表示一組樣本變數的分散程度;標準誤一般用於統計推斷中,主要包括假設檢驗和參數估計,如樣本平均數的假設檢驗、參數的區間估計與點估計等。
標準差與標準誤既有明顯區別,又密切相關:標準誤是標準差的1/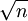 ;二者都是衡量樣本變數(觀測值)隨機性的指標,只是從不同角度來反映誤差;二者在統計推斷和誤差分析中都有重要的應用。
;二者都是衡量樣本變數(觀測值)隨機性的指標,只是從不同角度來反映誤差;二者在統計推斷和誤差分析中都有重要的應用。








這是標準差standard variation而不是standard error