風險調整貼現率法
出自 MBA智库百科(https://wiki.mbalib.com/)
風險調整貼現率法(Risk-adjusted Discount Rate/RADR)
目錄 |
風險調整貼現率法(Risk-adjusted Discount Rate,簡稱RADR)是將凈現值法和資本資產定價模型結合起來,利用模型依據項目的風險程度調整基準折現率的一種方法。
風險調整貼現率法的基本思路是:
對於高風險的項目採用較高的貼現率去計算凈現值,低風險的項目用較低的貼現率去計算,然後根據凈現值法的規則來選擇方案。因此,此種方法的中心是根據風險的大小來調整貼現率。該方法的關鍵在於根據風險的大小確定風險調整貼現率(即必要回報率)。
風險調整貼現率法的優點是比較符合邏輯,廣泛使用;在競爭的市場環境中,每種項目效益在將來不同的經濟狀態下會發生變化,風險調整貼現率法能夠通過調整項目在不同經濟狀態下的現金流貼現率,及時反映並規避市場風險。其優點如下:[1]
(1)在競爭的市場環境中,投資風險由整體經濟情況決定,投資多項目的方法不一定能夠降低市場風險。因此,較傳統方法而言,通過風險調整貼現率法,可以讓不同種類的項目具有不同的貼現率,從而投資於更具盈利能力或能更快收回投資成本的項目。[1]
(2)在傳統資源規劃中,只要公用事業單位謹慎投資,兼之生產的電能在制定的價格上存在需求,那麼資金成本就不會有任何風險。但是,在競爭的發電市場中,投資者會通過風險溢價來彌補可能出現的生產過剩所帶來的損失。風險調整貼現率法所確定的特定項目的資本成本或綜合資源規劃的資本成本比用公共事業資本成本所確定的更加精確。[1]
風險調整貼現率法的缺點是[2]:
①把時間價值和風險價值混在一起,並據此對現金流量進行折現,意味著風險隨時間的推移而加大,誇大了遠期風險。
②項目投資往往是期初投入,壽命期內收回,難以計算各年的必要回報率。傳統的風險調整貼現率法在運用時假定各年的必要回報率均一致,這樣的處理並不合理舊。
風險調整貼現率的計算公式為:K = i + bQ
式中:K——風險調整貼現率
i——無風險貼現率
b——風險報酬斜率
Q——風險程度
風險調整貼現率法的計算步驟:
1、風險程度的計算:
(1)計算方案各年的現金流入的期望值(E);
(2)計算方案各年的現金流入的標準差(d);
(3)計算方案現金流入總的離散程度,即綜合標準差(D);
(4)計算方案各年的綜合風險程度,即綜合變化繫數(Q)。
2、確定風險報酬斜率
(1)計算風險報酬斜率(b);
(2)根據公式:K =i +bQ 確定項目的風險調整貼現率;
(3)以“風險調整貼現率”為貼現率計算方案的凈現值,並根據凈現值法的規則來選擇方案。
風險調整貼現率法的案例分析[3]
某企業的最低報酬率為1 0%,要求的風險投資報酬率為15%,現有A、B、C三個投資方案,原始投資額分別為5000、2000、2000元。三個投資方案的現金流入量及概率如圖表5-10所示。
第一步,風險程度的計算。
A方案的現金流量的集中趨勢用期望值計算:
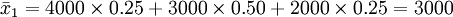 (元)
(元)
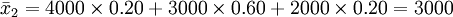 (元)
(元)
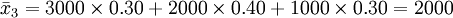 (元)
(元)
A方案現金流入的離散程度用標準差計算:
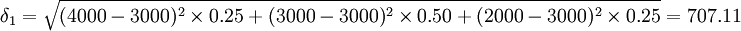 (元)
(元)
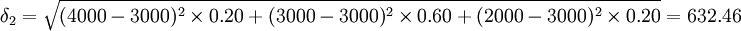 (元)
(元)
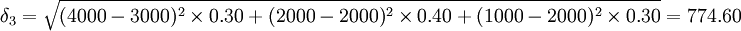 (元)
(元)
三年現金流入總的離散程度即綜合標準差,可從概率統計學得知:
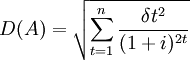
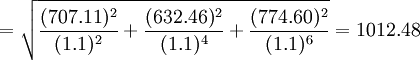 (元)
(元)
綜合標準差算出後,應計算變化繫數。為了綜合各年的風險,對具有一系列現金流入的方案用綜合變化繫數計算:
|
Q= | 綜合標準差 |
= |
| 現金流入預期現值 |
| D | ||
| EPV |
A方案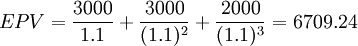 (元)
(元)
所以,A方案的風險程度
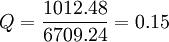
第二步,確定風險報酬斜率或貼現率。
b值是經驗數據,可根據歷史資料用高低或直線回歸法求得。假設中等風險程度項目變化繫數為0.5,則:
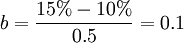
第一步已計算出了A方案的綜合變化繫數,A方案的風險調整貼現率為:
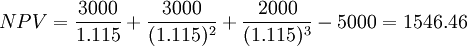 (元)
(元)
根據同樣方法,計算B、C方案:
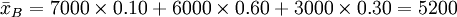 (元)
(元)
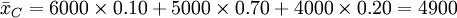 (元)
(元)
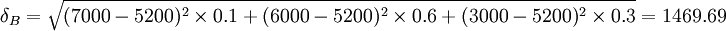 (元)
(元)
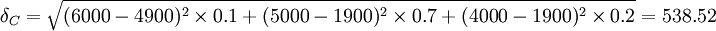 (元)
(元)
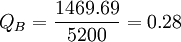
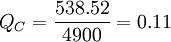
KB=10%+0.1×0.28=12.8%
KC=10%+0.1×0.11=11.1%
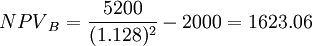 (元)
(元)
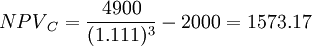 (元)
(元)
考慮了投資風險後,方案選優次序為B>C>A。如果不考慮投資風險,方案的優劣次序為B>A>C,計算如下:
A方案凈現值=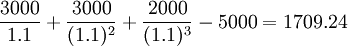 (元)
(元)
B方案凈現值=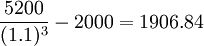 (元)
(元)
C方案凈現值=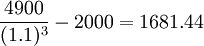 (元)
(元)
風險調整貼現法比較符合邏輯。不僅為理論家認可,而且使用廣泛。但是,把時間價值和風險價值混在一起,並據此對現金流雖進行貼現,意味著風險隨著時間的推延而加大,有時與事實不符。如飯店、果園等投資的前幾年現金流量難以預測,越往後越有把握。
評論(共8條)
"能更快收回投資成本的項目。" 在年收益率均相等的2個項目中,第一年回本的比第二年才一次過回本的要少賺。為何要追求收回成本快?
"能更快收回投資成本的項目。" 在年收益率均相等的2個項目中,第一年回本的比第二年才一次過回本的要少賺。為何要追求收回成本快?
資金的時間價值,早收回的錢可以再投資。
方案B和方案C的預期現值應該除以1.1^3吧,這樣才能與方案A比較,為何上面求QB的過程中直接用綜合標準差除以第三年的現金流期望值了呢?
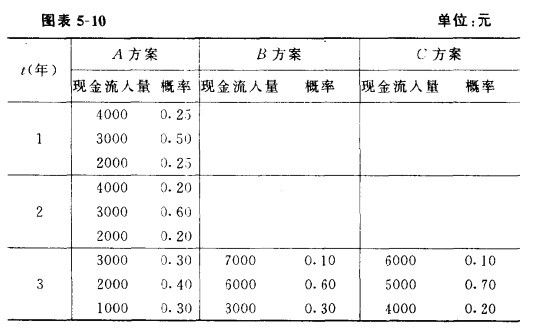








圖表5—10,在哪?