风险调整贴现率法
出自 MBA智库百科(https://wiki.mbalib.com/)
风险调整贴现率法(Risk-adjusted Discount Rate/RADR)
目录[隐藏] |
风险调整贴现率法(Risk-adjusted Discount Rate,简称RADR)是将净现值法和资本资产定价模型结合起来,利用模型依据项目的风险程度调整基准折现率的一种方法。
风险调整贴现率法的基本思路是:
对于高风险的项目采用较高的贴现率去计算净现值,低风险的项目用较低的贴现率去计算,然后根据净现值法的规则来选择方案。因此,此种方法的中心是根据风险的大小来调整贴现率。该方法的关键在于根据风险的大小确定风险调整贴现率(即必要回报率)。
风险调整贴现率法的优点是比较符合逻辑,广泛使用;在竞争的市场环境中,每种项目效益在将来不同的经济状态下会发生变化,风险调整贴现率法能够通过调整项目在不同经济状态下的现金流贴现率,及时反映并规避市场风险。其优点如下:[1]
(1)在竞争的市场环境中,投资风险由整体经济情况决定,投资多项目的方法不一定能够降低市场风险。因此,较传统方法而言,通过风险调整贴现率法,可以让不同种类的项目具有不同的贴现率,从而投资于更具盈利能力或能更快收回投资成本的项目。[1]
(2)在传统资源规划中,只要公用事业单位谨慎投资,兼之生产的电能在制定的价格上存在需求,那么资金成本就不会有任何风险。但是,在竞争的发电市场中,投资者会通过风险溢价来弥补可能出现的生产过剩所带来的损失。风险调整贴现率法所确定的特定项目的资本成本或综合资源规划的资本成本比用公共事业资本成本所确定的更加精确。[1]
风险调整贴现率法的缺点是[2]:
①把时间价值和风险价值混在一起,并据此对现金流量进行折现,意味着风险随时间的推移而加大,夸大了远期风险。
②项目投资往往是期初投入,寿命期内收回,难以计算各年的必要回报率。传统的风险调整贴现率法在运用时假定各年的必要回报率均一致,这样的处理并不合理旧。
风险调整贴现率的计算公式为:K = i + bQ
式中:K——风险调整贴现率
i——无风险贴现率
b——风险报酬斜率
Q——风险程度
风险调整贴现率法的计算步骤:
1、风险程度的计算:
(1)计算方案各年的现金流入的期望值(E);
(2)计算方案各年的现金流入的标准差(d);
(3)计算方案现金流入总的离散程度,即综合标准差(D);
(4)计算方案各年的综合风险程度,即综合变化系数(Q)。
2、确定风险报酬斜率
(1)计算风险报酬斜率(b);
(2)根据公式:K =i +bQ 确定项目的风险调整贴现率;
(3)以“风险调整贴现率”为贴现率计算方案的净现值,并根据净现值法的规则来选择方案。
风险调整贴现率法的案例分析[3]
某企业的最低报酬率为1 0%,要求的风险投资报酬率为15%,现有A、B、C三个投资方案,原始投资额分别为5000、2000、2000元。三个投资方案的现金流入量及概率如图表5-10所示。
第一步,风险程度的计算。
A方案的现金流量的集中趋势用期望值计算:
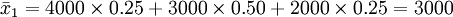 (元)
(元)
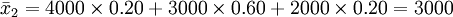 (元)
(元)
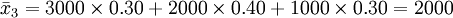 (元)
(元)
A方案现金流入的离散程度用标准差计算:
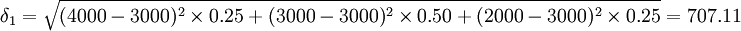 (元)
(元)
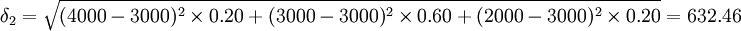 (元)
(元)
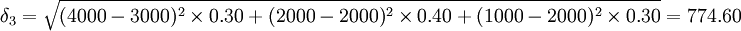 (元)
(元)
三年现金流入总的离散程度即综合标准差,可从概率统计学得知:
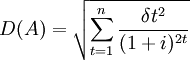
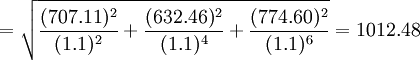 (元)
(元)
综合标准差算出后,应计算变化系数。为了综合各年的风险,对具有一系列现金流入的方案用综合变化系数计算:
|
Q= | 综合标准差 |
= |
| 现金流入预期现值 |
| D | ||
| EPV |
A方案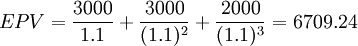 (元)
(元)
所以,A方案的风险程度
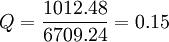
第二步,确定风险报酬斜率或贴现率。
b值是经验数据,可根据历史资料用高低或直线回归法求得。假设中等风险程度项目变化系数为0.5,则:
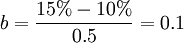
第一步已计算出了A方案的综合变化系数,A方案的风险调整贴现率为:
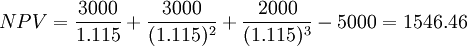 (元)
(元)
根据同样方法,计算B、C方案:
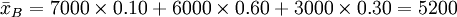 (元)
(元)
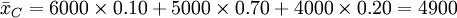 (元)
(元)
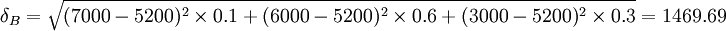 (元)
(元)
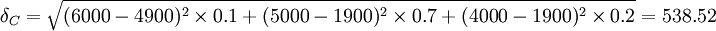 (元)
(元)
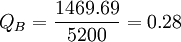
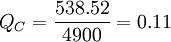
KB=10%+0.1×0.28=12.8%
KC=10%+0.1×0.11=11.1%
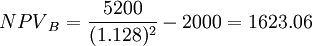 (元)
(元)
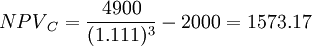 (元)
(元)
考虑了投资风险后,方案选优次序为B>C>A。如果不考虑投资风险,方案的优劣次序为B>A>C,计算如下:
A方案净现值=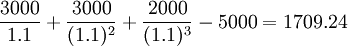 (元)
(元)
B方案净现值=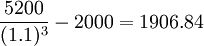 (元)
(元)
C方案净现值=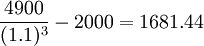 (元)
(元)
风险调整贴现法比较符合逻辑。不仅为理论家认可,而且使用广泛。但是,把时间价值和风险价值混在一起,并据此对现金流虽进行贴现,意味着风险随着时间的推延而加大,有时与事实不符。如饭店、果园等投资的前几年现金流量难以预测,越往后越有把握。
评论(共8条)
"能更快收回投资成本的项目。" 在年收益率均相等的2个项目中,第一年回本的比第二年才一次过回本的要少赚。为何要追求收回成本快?
"能更快收回投资成本的项目。" 在年收益率均相等的2个项目中,第一年回本的比第二年才一次过回本的要少赚。为何要追求收回成本快?
资金的时间价值,早收回的钱可以再投资。
方案B和方案C的预期现值应该除以1.1^3吧,这样才能与方案A比较,为何上面求QB的过程中直接用综合标准差除以第三年的现金流期望值了呢?

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 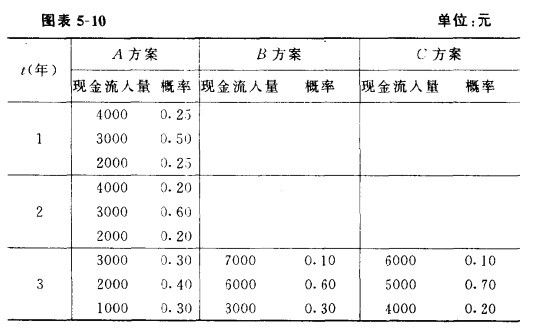















图表5—10,在哪?