統計預測

出自 MBA智库百科(https://wiki.mbalib.com/)

統計預測(statistical forecast/Statistical projections)

　　預測就是根據過去和現在估計未來，預測未來。

　　統計預測屬於預測方法研究範疇，即如何利用科學的統計方法對事物的未來發展進行定量推測，並計算概率置信區間。

　　統計預測方法是一種具有通用性的方法。

　　統計預測的三個要素：

　　1、實際資料是預測的依據；

　　2、經濟理論是預測的基礎；

　　3、數學模型是預測的手段。

　　一、統計預測、經濟預測的主要聯繫是：

　　1、它們都以經濟現象的數值作為其研究的對象；

　　2、它們都直接或間接地為巨集觀和微觀的市場預測、管理決策、制定政策和檢查政策等提供信息；

　　3、統計預測為經濟定量預測提供所需的統計方法論。

　　二、統計預測、經濟預測的區別

　　從研究的角度看，統計預測和經濟預測都以經濟現象的數值作為其研究對象，但著眼點不同。前者屬於方法論研究，其研究的結果表現為預測方法的完善程度；後者則是對實際經濟現象進行預測，是一種實質性預測，其結果表現為對某種經濟現象的未來發展做出判斷。

　　從研究的領域來看，經濟預測是研究經濟領域中的問題，而統計預測則被廣泛地應用於人類活動的各個領域。

　　1、在市場經濟條件下，預測的作用是通過各個企業或行業內部的行動計劃和決策來實現的;

　　2、統計預測作用的大小取決於預測結果所產生的效益的多少。

　　影響預測作用大小的因素主要有：

　　1、預測費用的高低；

　　2、預測方法的難易程度；

　　3、預測結果的精確程度。

　　1、統計預測方法可歸納分為定性預測方法和定量預測方法兩類，其中定量預測法又可大致分為回歸預測法和時間序列預測法;

　　2、按預測時間長短分為近期預測、短期預測、中期預測和長期預測;

　　3、按預測是否重覆分為一次性預測和反覆預測。

　　統計預測法的內容主要包括：對預測資料的初步分析；確定適用的預測模型和估計模型參數；列出預測公式，進行外推預測；對預測結果加以統計分析，不斷改進預測。

　　對所掌握的時間數列資料，既可就此數列進行外推預測，也可結合有聯繫的數列進行回歸外推預測。作為第一步，通常先畫成動態折線圖或回歸散點圖，從圖形上判斷適用的預測模型，然後估計模型參數。

　由於統計預測是著眼於未來的，而時間數列中的近期數值與遠期數值對測定未來的作用不同，一般近期值的作用較大。為此，統計預測法要求對近期值比對遠期值給以較大的權數，進行合理加權。

　　統計預測法使用最多的是指數折扣加權法，即以其值在0與1之間的折扣繫數a為底，用a^r作權數，指數r的值從0到t-1（t為數列時期數），隨著r值的增大,a^r值遞減，a⁰＝1是用於最近值的最大權數，以後用a¹、a²、a³、…依次對從近到遠的數值加權，權數越來越小。指數加權的對象有兩種:

• 直接對各期水平x加權，求加權平均數；
• 對各期預測誤差e的平方加權,求加權總和數。前者發展為指數平滑法，後者發展為折扣最小平方法。

　　1）指數平滑法。其基本算式是：

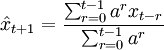
　　式中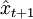為t+1期預測值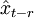，為t-r期觀察值。當t很大時，a^t接近零，可略去。上式經推導得出：

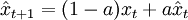
　　以α代表平滑繫數，設α=1-a，則上式可寫成如下遞推公式：

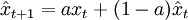
　　此式可直接用於外推預測，非常方便，既可及時更新資料，又可把資料儲存減少到只存一個舊預測值 。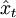

　　2)折扣最小平方法。其數學要求是：

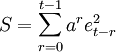　　　　　　　　　　=最小值

　　式中預測誤差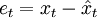。用此法求解直線方程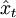＝a+bt中的a、b參數時，仍用最小平方法的公式，只是式中的每項數值都用a^r加權計算，並用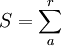代替n,然後根據具體化的預測公式進行預測。

　　根據預測公式進行預測時，時間數列模型可直接外推預測，回歸模型則需要先用適當的公式取得自變數時間數列的預測值，然後再求因變數預測值。

　　在預測的統計分析中，要計算誤差綜合指標，作為評價和比較各種預測模型和預測方法的依據。常用的指標是均方誤差（MSE）和均方根誤差（RMSE），其算式是：

　　　　　　　　　　MSE=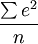

　　　　　　　　　　RMSE=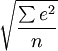

　　選擇統計預測方法時，主要考慮下列三個問題：

　　1、合適性

　　2、費用

　　3、精確性

方法	時間範圍	適用情況	電腦硬體最低要求	應做工作
定性預測法	短、中、長期	對缺乏歷史統計資料或趨勢面臨轉折的事件進行預測	計算器	需做大量的調查研究工作
一元線性回歸預測法	短、中期	自變數與因變數之間存線上性關係	計算器	為兩個變數收集歷史數據，此項工作是此預測中最費時的
多元線性回歸預測法	短、中期	因變數與兩個或兩個以上自變數之間存線上性關係	在兩個自變數情況下可用計算器，多於兩個自變數的情況下用電腦	為所有變數收集歷史數據是此預測中最費時的
非線性回歸預測法	短、中期	因變數與一個自變數或多個其它自變數之間存在某種非線性關係	在兩個變數情況下可用計算器，多於兩個變數的情況下用電腦	必須收集歷史數據，並用幾個非線性模型試驗
趨勢外推法	中期到長期	當被預測項目的有關變數用時間表示時，用非線性回歸	與非線性回歸預測法相同	只需要因變數的歷史資料，但用趨勢圖做試探時很費時
分解分析法	短期	適用於一次性的短期預測或在使用其他預測方法前消除季節變動的因素	計算器	只需要序列的歷史資料
移動平均法	短期	不帶季節變動的反覆預測	計算器	只需要因變數的歷史資料，但初次選擇權數時很費時間
指數平滑法	短期	具有或不具有季節變動的反覆預測	在用電腦建立模型後進行預測時，只需計算器就行了	只需要因變數的歷史資料，是一切反覆預測中最簡易的方法，但建立模型所費的時間與自適應過濾法不相上下
自適應過濾法	短期	適用於趨勢型態的性質隨時間而變化，而且沒有季節變動的反覆預測	電腦	只需要因變數的歷史資料，但制定並檢查模型規格很費時間
平穩時間序列預測法	短期	適用於任何序列的發展型態的一種高級預測方法	電腦	計算過程複雜、繁瑣
干預分析模型預測法	短期	適用於當時間序列受到政策干預或突發事件影響的預測	電腦	收集歷史數據及影響時間
景氣預測法	短、中期	適用於時間趨勢延續及轉折預測	電腦	收集大量歷史資料和數據並需大量計算
灰色預測法	短、中期	適用於時間序列的發展呈指數型趨勢	電腦	收集對象的歷史數據
狀態空間模型和卡爾曼濾波	短、中期	適用於各類時間序列的預測	電腦	收集對象的歷史數據並建立狀態空間模型

　　在統計預測中的定量預測要使用模型外推法，使用這種方法有以下兩條重要的原則：

　　連貫原則，是指事物的發展是按一定規律進行的，在其發展過程中，這種規律貫徹始終，不應受到破壞，它的未來發展與其過去和現在的發展沒有什麼根本的不同；

　　類推原則，是指事物必須有某種結構，其升降起伏變動不是雜亂無章的，而是有章可循的。事物變動的這種結構性可用數學方法加以模擬，根據所測定的模型，類比現在，預測未來。