灰色預測法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
灰色預測法是一種對含有不確定因素的系統進行預測的方法。灰色系統是介於白色系統和黑色系統之間的一種系統。
白色系統是指一個系統的內部特征是完全已知的,即系統的信息是完全充分的。而黑色系統是指一個系統的內部信息對外界來說是一無所知的,只能通過它與外界的聯繫來加以觀測研究。灰色系統內的一部分信息是已知的,另一部分信息時未知的,系統內各因素間具有不確定的關係。
灰色預測通過鑒別系統因素之間發展趨勢的相異程度,即進行關聯分析,並對原始數據進行生成處理來尋找系統變動的規律,生成有較強規律性的數據序列,然後建立相應的微分方程模型,從而預測事物未來發展趨勢的狀況。其用等時距觀測到的反應預測對象特征的一系列數量值構造灰色預測模型,預測未來某一時刻的特征量,或達到某一特征量的時間。
①灰色時間序列預測;即用觀察到的反映預測對象特征的時間序列來構造灰色預測模型,預測未來某一時刻的特征量,或達到某一特征量的時間。
②畸變預測;即通過灰色模型預測異常值出現的時刻,預測異常值什麼時候出現在特定時區內。
③ 系統預測;通過對系統行為特征指標建立一組相互關聯的灰色預測模型,預測系統中眾多變數間的相互協調關係的變化。
④拓撲預測;將原始數據作曲線,在曲線上按定值尋找該定值發生的所有時點,並以該定值為框架構成時點數列,然後建立模型預測該定值所發生的時點
在建立灰色預測模型之前,需先對原始時間序列進行數據處理,經過數據處理後的時間序列即稱為生成列。灰色系統常用的數據處理方式有累加和累減兩種。
1、關聯繫數
1、設時間序列![]() 有n個觀察值,
有n個觀察值,![]() ,通過累加生成新序列
,通過累加生成新序列![]() , 則GM(1,1)模型相應的微分方程為:
, 則GM(1,1)模型相應的微分方程為:
其中:α稱為發展灰數;μ稱為內生控制灰數。
2、設![]() 為待估參數向量,
為待估參數向量,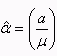 ,可利用最小二乘法求解。解得:
,可利用最小二乘法求解。解得:
求解微分方程,即可得預測模型:
3、模型檢驗
灰色預測檢驗一般有殘差檢驗、關聯度檢驗和後驗差檢驗。
1、殘差模型:若用原始經濟時間序列![]() 建立的GM(1,1)模型檢驗不合格或精度不理想時,要對建立的GM(1,1)模型進行殘差修正或提高模型的預測精度。修正的方法是建立GM(1,1)的殘差模型。
建立的GM(1,1)模型檢驗不合格或精度不理想時,要對建立的GM(1,1)模型進行殘差修正或提高模型的預測精度。修正的方法是建立GM(1,1)的殘差模型。
2、GM(n,h)模型
GM(n,h)模型是微分方程模型,可用於對描述對象作長期、連續、動態的反映。從原則上講,某一灰色系統無論內部機制如何,只要能將該系統原始表徵量表示為時間序列![]() ,並有
,並有![]() , (N表數自然數集),即可用GM模型對系統進行描述。
, (N表數自然數集),即可用GM模型對系統進行描述。
案例一:灰色預測法在百亞集團連鎖企業的應用[1]
商業連鎖企業隨著門店的不斷增加,總部對企業的管理將變得越發困難,尤其是對銷售量的預測,這嚴重影響了決策層對企業的控制和管理,影響總部的決策水平,包括資金的調度和使用、大批量進貨以降低成本、門店的發展速度等等。隨著模糊數學的不斷發展,灰色預測方法得到了廣泛應用,它對於商業連鎖企業的銷售管理,有指導價值。
一、灰色預測原理
灰色預測是灰色系統理論的重要組成部分,它利用連續的灰色微分模型,對系統的發展變化進行全面的觀察分析,並做出長期預測。
灰色系統是部分信息已知、部分未知的系統。同時,灰色系統理論將隨機過程看作是在一定範圍內變化的與時間有關的灰色過程,將隨機變數看成是在一定範圍內變化的灰色量,顯然,商品零售業就是一個灰色過程,商品銷售系統就是一個灰色系統,銷售量就是一個灰色量。
灰色系統理論認為,灰色系統的行為現象儘管是朦朧的,數據是雜亂的,但畢竟是有序的是有整體功能的,因而對變化過程可作科學預測。在灰色理論中,用來發掘這些規律的適當方式是數據生成,將雜亂的原始數據整理成規律性較強的生成數列,再通過一系列運算,就可以建立灰色理論中一階單變數微分方程的模型即CM(1,1)模型。
下麵根據百亞集團1995年至2000年門店分類商品銷售額數據建立GM(1,1)模型,並預測百亞集團在今後幾年裡的門店分類銷售額。
百亞集團門店歷年商品分類平均銷售狀況表(單位10萬元)。
| 年份 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 類別 | ||||||
| 食品類 | 223.3 | 227.3 | 230.5 | 238.1 | 242.9 | 251.1 |
| 煙酒類 | 37.9 | 39.8 | 45.4 | 46.2 | 46.9 | 50.9 |
| 洗化類 | 34.4 | 35.1 | 35.5 | 36.5 | 37.2 | 38.0 |
| 服針紡 | 8.6 | 8.7 | 8.8 | 9.1 | 9.0 | 9.4 |
| 文娛類 | 12.0 | 12.6 | 13.7 | 13.9 | 14.2 | 15.4 |
| 日雜類 | 27.5 | 27.8 | 27.2 | 27.8 | 28.5 | 29.3 |
二、模型的實際應用
據上表的原始數據列:
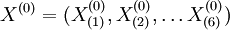
=(223.3,227.3,230.5,238.1,242.9,251.1)
作一次累加生成,得生成數列:
X(1) = (223.3,450.6,681.1,919.2,1162.1,1413.2)
建立數據矩陣B及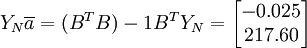
即a=-0.025 u=217.6 u/a=-8705.0
故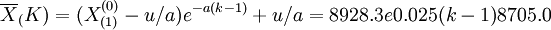 (1)
(1)
在該模型中,依次取K=1,2,3,4,5,6可以得到各生成數據的模型計算值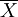 (1)及還原為原始數據的模型計算值X(0)。
(1)及還原為原始數據的模型計算值X(0)。
生成數對照表
| 序號 | 1 | 2 | 3 | 4 | 5 | 6 |
| 模型計算值 | 223.3 | 449.3 | 681.7 | 918.7 | 1162.3 | 1412.1 |
| 實際值 | 223.4 | 450.6 | 681.1 | 919.2 | 1162.1 | 1413.2 |
還原數對照表
| 序號 | 1 | 2 | 3 | 4 | 5 | 6 |
| 年份 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 |
| 模型計算值 | 223.3 | 226 | 232.4 | 237 | 243.6 | 249.8 |
| 實際值 | 223.3 | 227.3 | 230.5 | 238.1 | 242.9 | 251.1 |
| 相對誤差 | 0 | -0.57 | 0.82 | -0.46 | 0.29 | -0.48 |
從上面的經驗可以看出a=-0.025,且接近於0,說明本系統採用灰色預測的方法是適合的,數據檢驗表明最大誤差為0.82%,擬合精度較高。
令K=9,則X(0)(2003)=2693萬元
K=14,則X(0)(2008)=3051萬元
可以預測到2008年,百亞連鎖店的門店食品類商品銷量將達到3051萬元左右,用同樣的方法,可以求得百亞集團連鎖店各類商品銷售量的預測模型。
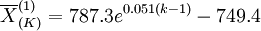 (2)
(2)
 (3)
(3)
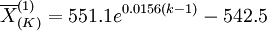 (4)
(4)
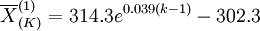 (5)
(5)
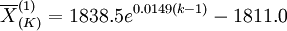 (6)
(6)
在上面的6個預測模型中所有的a<0,且接近於0,說明本系統採用灰色預測方法是適合的,擬合度應當較高。
代入上述預測模型,就可以預測到2003年以及2008年百亞連鎖集團門店商品分類銷售狀況,這對於提高總部的商品批量進貨決策、門店發展決策、資金的調度和使用以及規範化管理具有重要意義。
灰色預測法預測門店分類商品銷售額(單位:10萬元)
| 2001 | 2003 | 2008 | |
| 食品類 | 256.1 | 269.3 | 305.1 |
| 煙酒類 | 53.1 | 58.8 | 75.9 |
| 洗化類 | 38.4 | 39.5 | 43.1 |
| 服針紡 | 9.5 | 9.7 | 10.4 |
| 文娛類 | 15.3 | 16.4 | 19.9 |
| 日雜類 | 29.7 | 30.6 | 33 |
- ↑ 李春剛.灰色預測法在商業連鎖企業的應用[J].經濟師,2001,(12)

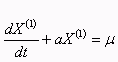
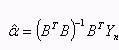








長知識啊!