商品銷售量
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
什麼是商品銷售量[1]
商品銷售量是指貿易企業向其以外的單位和個人出售(包括對境外直接出口)商品的數量(金額)。
影響商品銷售量變動的因素[2]
影響商品銷售量變動的因素很多,在商品貨源可以充分保證的情況下,企業的商品銷售量主要受三個方面的因素制約:
1.消費者需求因素
消費者需求因素包括消費者數量及構成、購買力水平、購買動機等,對商品銷售量大小有決定性的影響。一般地說,在其他條件不變的情況下,商品銷售量與消費人口數量成正比關係。但在一定的商圈範圍內,消費者構成不同,其購買力水平不同、購買動機不同、消費結構存在一定的差異,對不同商品的銷售量大小有明顯影響。
2.市場競爭因素
市場競爭因素包括同類商品的市場投放量、市場需求飽和程度、新老產品更新換代情況、同類企業之間的競爭態勢都會對企業的銷售量帶來影響。一般地講,市場同類商品投放量越大、需求飽和程度越高,企業的銷售量會相應減少;新產品上市,會削弱老產品的銷售量;競爭對手數量增加或者實力增強,也會減少企業同類產品的市場銷售量。
3.企業經營因素
企業經營因素主要指企業的經濟實力、職工素質、促銷能力及占有的市場份額,對銷售量有直接影響。一般地說,企業經濟實力強、職工素質高、促銷方式靈活、市場占有份額大,銷售量相應也大;反之亦然。
商品銷售量變化的規律性[2]
儘管影響商品銷售量變動的因素很多,但通過銷售量變動的歷史資料分析可以發現,任何一種商品的銷售量變動都有一定的規律性。歸納起來,在正常情況下,一種商品的銷售量變化大致有以下6種類型:
1.銷售量均衡增長,逐期擴大
這種趨勢,對處於成長期的產品來說,表現尤為明顯。若用坐標圖顯示,其銷售量表現為一條呈上升趨勢的曲線。
2.銷售量起伏變化大體平穩
這種趨勢,對處於成熟期的產品來說,表現更為明顯。若用坐標圖顯示,其銷售量表現為一條波浪式的曲線。
3.銷售量變化不規則,但總體上趨於增長
這種趨勢,若用坐標圖顯示,表現為一條不規則的、總體上呈上升趨勢的曲線。
4.銷售量受相關產品制約大,隨相關產品銷售量變化
具有正相關和負相關兩種情況。前者如房屋裝修材料的銷售量與房屋建築規模(面積)呈正相關關係;後者如陶瓷用品與塑料用品的銷售量呈負相關關係。
5.銷售量受季節性影響大,隨季節變化
而周期性變化 如各種時令性商品、節日用品、旅游用品等,其銷售量變化不僅具有上述某種類型特征,而且兼有明顯的季節性特點。如用坐標圖顯示,其銷售量的季節性變化趨勢在企業各個經營周期(或年份)中相同。
6.銷售量受產品經濟壽命周期影響,呈拋物線變化
如產品在試銷期的銷售量緩慢增長,中期快速增長,衰退期銷售量下降,用坐標圖顯示,表現為一條拋物線。
商品銷售量(額)及變化趨勢預測[3]
企業在計劃期間究竟能銷售多少,必須通過市場調查,進行科學的銷售預測。銷售預測是根據市場上供需情況的發展趨勢,以及本企業的銷售單價、推銷活動、產品改進、分銷途徑等方面的計劃安排,來對該項商品在計劃期間的銷售量或銷售額所做出的預計或估量。
商品銷售量(額)及變化趨勢預測常見的技術方法是趨勢預測分析法。它是應用事物發展的連續性原理來預測事物發展的趨勢。其方法是:首先把本企業過去的銷售歷史資料按時間順序排列下來;然後運用數理統計的方法預計、推測計劃期間的銷售數量或銷售金額,也稱時間序列預測分析法。
這類方法的優點是收集信息方便、迅速;缺點是對市場情況的變動未加考慮。根據採用的具體數學方法的不同,又分為算術平均法、移動加權平均法、指數平滑法和回歸分析法。
- 一、算術平均法
以過去若幹時期的銷售量或銷售金額的算術平均數作為計劃期的銷售量(銷售額)。計算公式為:
計劃期銷售量(銷售額)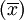 = = |
|
【例1】甲公司今年上半年乙產品銷售量的資料如下。要求預測7月份的乙產品銷售量。
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 乙產品(萬斤) | 138 | 136 | 142 | 134 | 146 | 144 |
7月份的乙產品銷售量=(138+136+142+134+146+144)/6=140(萬斤)
這種方法的優點是計算簡便,但它使各個月份的銷售差異平均化,特別是沒有考慮到近期的變動趨勢,因而測出的預計數與實際數可能發生較大誤差。
註意這種方法的適用條件:適用於銷售量(銷售額)比較穩定的商品,如沒有季節性的食品、文具、日常用品等。
- 二、加權平均法
根據過去若幹時期的銷售量或銷售金額,按其距計劃期的遠近分別進行加權,然後計算其加權平均數,據以作為計劃期的銷售預測數。
註意:所取的觀察值應隨時間的推移而順延。預測8月份,則以5、6、7三個月的歷史資料為依據。接近計劃期的實際銷售情況對計劃期預計數的影響較大。近期確定的加權數大,遠期確定的權數小。
加權平均法的計算公式為:計劃期銷售量(銷售額)(</math>(\overline x)</math>)=各期銷售量(銷售額)分別乘其權數之和(∑wx)
【例2】依[例1]資料,要求預測7月份的乙產品銷售量。
預測7月份的乙產品銷售量我們選取4、5、6三個月的歷史資料來計算。
令w1=0.2;w2=0.3;w3=0.5
預測7月份的乙產品銷售量=134×0.2+146×0.3+144×0.5=142.6(萬斤)
- 三、指數平渭法
指數平滑法實質上也是一種加權平均法。導入平滑繫數α,前期實際銷售量(銷售額)乘以α,前期預測的銷售量(銷售額)乘以(1-α),這兩個乘積相加得到本期預測銷售量(銷售額)。選取α值大於0,小於1,一般取值為0.3-0.7。選取的平滑繫數越大,則近期實際數對預測結果的影響越大;選取的平滑繫數越小,則近期實際數對預測結果的影響越小。
註意:選取較小的平滑繫數計算的結果能反映觀察值變動的長期趨勢;選取較大的平滑繫數計算的結果能反映觀察值變動的新近趨勢。指數平滑法計算公式為:
計劃期銷售量(銷售額)(</math>(\overline x)</math>)=平滑繫數×上期實際銷售數+(1-平滑繫數)×上期預測銷售數
【例3】依[例1)資料,甲公司6月份的實際銷售量為144萬斤,原來預測6月份的銷售量為148萬斤,平滑繫數採用0.7。要求按指數平滑法預測7月份的乙產品銷售量。
預測7月份的乙產品銷售量=0.7×144+(1-0.7)×148=145.2(萬斤)
- 四、回歸分析法
回歸分析法是根據直線方程式y=a+bx,按照數學上最小平方法的原理來確定一條能正確反映自變數x與因變數y之間具有誤差的平方和最小的直線,這條直線為回歸直線。
直線方程式y=a+bx中常數項。與繫數占的值可按下列公式計算:
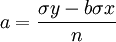
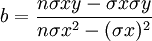
回歸分析法應用到銷售預測,可用y代表銷售量(銷售額),x代表間隔期(觀察期)。
由於觀察期是按時間順序排列的,間隔期相等,故可以採用簡捷的辦法,令∑x=0來求回歸線。具體說,如果實際觀察的期數為奇數,則取x的間隔期為1;如果實際觀察的期數為偶數,則取x的間隔期為2。確定間隔期的具體做法如下:
當實際觀察的期數為奇數時,取x的間隔期為1,如表2所示。
| 觀察期 | 間隔期(x) |
| 1 2 3 4 5 | -2 -1 0 1 2 |
| n=5 | ∑x=0 |
當實際觀察的期數為偶數,取x的間隔期為2,如表3所示。
| 觀察期 | 間隔期(x) |
| 1 2 3 4 5 6 | -5 -3 -1 1 3 5 |
| n=6 | ∑x=0 |
根據上述∑x=0的確定,a與b的值的公式可簡化為:
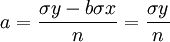
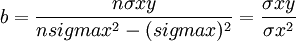
【例4】依[例1)資料,要求預測7月份的銷售量。
| 月份 | 間隔期(x) | 銷售量(y) | xy | x^2 |
| 1 2 3 4 5 6 | -5 -3 -1 1 3 5 | 138 136 142 134 146 144 | -690 -408 -142 134 438 720 | 25 9 1 1 9 25 |
| n=6 | ∑x=0 | ∑y=840 | ∑xy=52 | ∑x^2=70 |
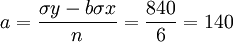
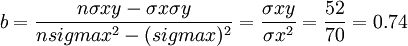 所以y=a+bx=140+0.74×7=145.18(萬斤)
所以y=a+bx=140+0.74×7=145.18(萬斤)
(註意這裡的間隔期確定為7。)
【例5】依[例4—1)資料,如果不考慮1月份的基本資料,要求根據2—6月份基本資料預測7月份的銷售量。
| 月份 | 間隔期(x) | 銷售量(y) | xy | x^2 |
| 2 3 4 5 6 | -2 -1 0 1 2 | 136 142 134 146 144 | -272 -142 0 146 288 | 4 1 0 1 4 |
| n=5 | ∑x=0 | ∑y=702 | ∑xy=20 | ∑x^2=10 |
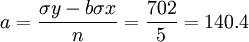
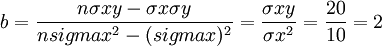
所以y=a+bx=140.4+2×3=146.4(萬斤)
(註意盆單的間隔期的確定為3。)







