分解分析法
出自 MBA智库百科(https://wiki.mbalib.com/)
目錄 |
分解分析法指將一複雜的事物分解為多個比較簡單的事物，將大系統分解為具體的組成要素，從中分析可能存在的風險及潛在損失的威脅。失誤樹分析方法是以圖解表示的方法來調查損失發生前種種失誤事件的情況，或對各種引起事故的原因進行分解分析，具體判斷哪些失誤最可能導致損失風險發生。
例如，可將匯率風險分解為匯率變化率、利率變化率、收益率期間結構等影響因素，然後對每一種影響因素作進一步的分析。
分解分析法的案例分析[1]
現有A、B兩因素分組資料如下表，A因素有a個水平，B因素有b個水平。設A因素有a-p個水平中的某些處理缺失數據，a-p>1;因素B有b-p個水平的某些處理缺失數據，b-p>1。如果a-p=1，那麼在劃分資料時，需要將該因素其它的一個或二個水平划到處理數據缺失的水平資料中，以估計水平間的交互作用效應、平方和分量方差組分等。
將上述資料等重覆和不等重覆的處理分開，並設劃分後的兩因素完全交叉處理內等重覆資料，A因素包括p個水平，B因素包括q個水平，重覆數為r，含pqr個觀測值；處理內不等重覆資料A因素有a-p個水平，B因素有b-p個水平，共N個觀測值。
- 1.F檢驗
對於有交互作用的雙向分類資料，假設各因素均為固定效應，我們感興趣的是考慮因數A的a個水平和B個水平以及交互作用間是否有差異。這歸結為檢驗假設：
HAB：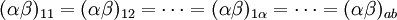
或HA：
或HB：
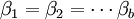
當H_{AB}、H_A或H_B為真時構造統計量：
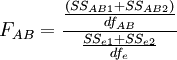——F(dfAB,dfe)
——F(dfA,dfe)
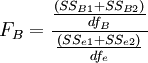——F(dfB,dfe)
其中dfAB = (p − 1)(q − 1) + (a − p − 1)(b − q − 1)dfA = a − 2,dfB = b − 2,dfe = N + pq(r − 1) − (a − p)(b − q)
給定顯著水準α，若F > Fα則表明差異顯著，否定H0，否則接受H0。
- 2.方差組分的估計
若兩因素效應為隨機時，研究者的主要興趣是獲得各方差組分的無偏估計而不是顯著性檢驗。
通過對上表中的等重覆與不等資料各平方和分量，分別求數學期望，合併相同方差組分有：
![(\alpha-2)^2_{\sigma_e}+\left[r(p-1)+(a-p-1)k_4\right]^2_{\sigma_{\alpha\beta}}+\left[(p-1)pr+(a-p-1)k_5\right]^2_{\sigma_{\alpha}}=SS_{B1}+SS_{B2}](/w/images/math/c/4/0/c40cab827af5fcb77d43959ec1ad8279.png)
![(b-2)^2_{\sigma_e}+\left[r(q-1)+(b-q-1)k_2\right]^2_{\sigma_{\alpha\beta}}+\left[(q-1)(p-1)qr+(b-q-1)k_1\right]^2_{\sigma_\alpha}=SS_{B1}+SS_{B2}](/w/images/math/0/6/f/06f8e57856b3ab0e4191a070ce1a5746.png)
![\left[(q-1)(p-1)+(a-p-1)(b-q-1)\right]^2_{\sigma_e}+\left[(q-1)(p-1)r+(a-p-1)(b-q-1)k_1\right]^2_{\sigma_{\alpha\beta}}=SS_{AB1}+SS_{AB2}](/w/images/math/3/3/2/332b9f479058c1971b6258cf28e7462b.png)
![\left[N+pq(r-1)-(a-p)(b-q)\right]^2_{\sigma_e}=SS_{e1}+SS_{e2}](/w/images/math/f/e/9/fe9b2f7b9015dc23b212e5984da8dc01.png)
解此方程組，不論所劃分的兩部分之間有否相關都可以估計出各因數方差組分的大小。
- 3.方法的拓廣與總結
對多因素少數水平處理髮生數據缺失的資料，劃分的方法可能不僅一種，比如，某一因素的一個水平有幾個處理缺失了數據，而這幾個處理也屬於另一因素的幾個水平，則劃分只在一個因素內進行即可。
同理可以證明，任何一個多因素次級樣本含量全不等資料，在各因素水平間，交互作用間不存在相關的條件下，都可以沿一個因素或幾個因素劃分成幾個部分，分別採用最小二乘分析法求出各部分資料的觀測值所包含的各種效應、平方和分量和方差組分等，爾後再合併估計與比較檢驗。
採用上文方法，可比對整個資料實施最小二乘分析降低正規方程繫數矩陣階數p+q+pq階，如果對整個處理數皆不等的資料進行分解分析，效果更為可觀。
如果將所劃分的每部分資料看作一個單元，次級樣本含量等資料的分解分析法實質是單元內統計方法的一個特例。其特殊之處在於對每個單元的統計分析方法不盡相同。因此從這個意義上講，分解分析法在生物科學研究中必將具有廣泛的使用價值。
- ↑ 王義通 孫巨集雁.次級樣本含量不等資料的分解分析法.黑龍江畜牧獸醫.2001年第7期
