灰色決策

出自 MBA智库百科(https://wiki.mbalib.com/)

　　灰色決策是指運用灰色系統理論，就灰色系統(信息部分明確，部分不明確的系統)中的決策問題進行的決策，層次分析決策指將複雜問題中的各種因素通過劃分相互聯繫的有序層次使之條理化，然後根據某些判斷準則就每一層次的元素的相對重要性賦予定量化的度量，其後依據數學方法推算出各個元素的相對重要性權值和排序，最後對結果進行研究、分析與調查的決策。

　　某一研究範圍內的備選方案全體記為A={A₁, A₂, ...,A_n};指標因素集合記為S={S₁,S₂,...,S_m}.方案A_i在指標場下的效果評價值為非負區間灰數,i=1,2,...,n;j=1,2,...,m)，方案A_i的效果評價向量記為

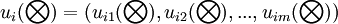　　(i=1,2,...,n) (1)

　　為了消除量綱和增加可比性，用灰色極差變換

　　對效益型指標值

　　,

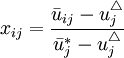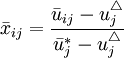
　　對成本型指標值

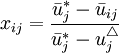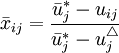　　, (2)

　　其中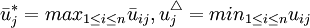(j=1,2,...,m),對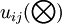(i=1,2,...,m)進行標準化處理.

　　定義1：設標準化後的個方案效果評價向量為

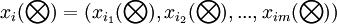　　(i=1,2,...,n)　　 　　　　(3)

　　其中均為[ 0, 1]上的非負區間灰數.記

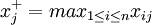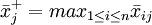　　,,(j=1,2...,m)　　　　　　(4)

　　則稱m維非負區間灰數向量

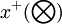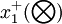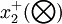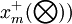　　=(,,..., 　　　　　　(5)

　　為理想方案效果評價向量，其中x_j^{+}(\bigotimes)\in [x_j^{+},\bar{x}_j^{+}]</math>(j=1,2...,m)

　　定義2(灰色區間關聯繫數)設標準化後的各方案效果評價向量及理想方案效果評價向量為定義1中式(3)和式(5)所示，則稱

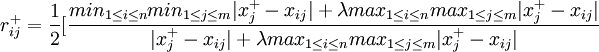
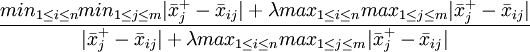+ (6)

　　為子因素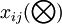關於理想母因素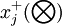的灰色區間關聯繫數(i=1,2,...,n;j=1,2,...m)，其中為分辨繫數或比較環境調節因數.

　　由定義2可知，理想方案效果評價值關於理想母因素的關聯繫數構成向量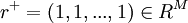.當決策問題中方案的指標評價值均為清晰數(即白數)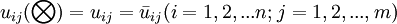時，所定義的灰色區間關聯繫數化為文灰色關聯繫數.所以經典灰色關聯繫數公式是灰色區間關聯繫數公式的特例.

　　定義3(灰色區間相對關聯繫數)設標準化後的各方案效果評價向量及理想方案效果評價向量由定義1中式(3)和式(5)給出，記

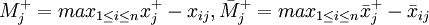　　 (7)

　　由定義3可知，理想方案效果評價值關於理想母因素的灰色區間相對關聯繫數構成向量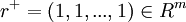

　　1、研究了灰色決策問題的區間關聯和區間聚類分析方法：提出了灰色區間關聯繫數公式和灰色區間相對關聯繫數公式，構建了幾種關聯度決策演算法，對不完全信息下灰色區間關聯決策方法進行了研究。

　　2、在經典灰色規劃的基礎上，對灰色動態規劃、灰色多目標規划算法、灰色正項幾何規劃進行了研究：提出了灰色動態規劃、θ動態定位規劃及其最優解的概念，構建了灰色動態規劃及θ動態定位規劃最優解的演算法。對一般意義上的灰色多目標規劃，提出了客觀確定子目標權重的方法及修正方法，利用子目標的權重引入了各個子目標取最優值的白化權函數，構建了灰色多目標規劃有效解及其θ定位規劃最優解的演算法。提出了灰色正項幾何規劃、θ定位幾何規劃及其準優解和最優解的概念，構建了灰色正項幾何規劃準優解的演算法。算例說明瞭演算法的合理性和可行性。

　　3、對灰色風險型決策方法進行了研究：提出了灰色多指標風險型決策的概念,對指標權重完全未知且指標值為區間灰數的風險型多指標決策問題,給出了灰色模糊關係法及雙基點法兩種決策方法,利用信息熵確定的屬性權重使決策方法更符合客觀要求。提出了具有交易費用的灰色組合投資模型的有效解及其臨界最優解和均值白化最優解的概念。

　　4、對灰色模糊決策方法進行了研究：提出了基於灰色模糊信息的多屬性決策的概念,構建了灰色模糊多屬性決策問題的演算法,直接由灰色模糊決策矩陣確定變權的基礎權重和上確界,使演算法在理論上更加嚴謹可靠。提出了灰色群決策問題的概念,給出了灰色群決策問題的解法,通過實例對解法的合理性進行了說明與分析。建立了基於灰色模糊關係的多屬性群體決策方法,分別對屬性權重向量已知和未知兩種情況給出了簡便實用的演算法。最後,通過算例說明瞭各種演算法的合理性。

　　5、對灰色粗糙決策方法進行了研究：提出了基於灰色綜合決策權的決策表離散化方法,對應用決策表方法解決實際問題時可能出現的問題進行了有益的探討,指出約簡過程要註意理論與實際相結合、定性與定量相結合,才能得到貼近實際的決策規則。

　　6、對灰色博弈決策方法進行了研究：提出了二人有限零和灰色博弈的概念,建立了帶有灰色約束的二人有限零和博弈模型和博弈平衡解優序關係的確定方法,該方法與傳統方法的不同之處在於,在灰色博弈模型中,考慮了博弈雙方在選擇自身的策略時受到了某個灰色不確定性約束。提出了具有混合策略的二人有限零和灰色博弈的概念,構建了具有混合策略的二人有限零和灰色博弈模型及其平衡解的求解方法。實例說明瞭有關概念及結論的合理性與求解方法的有效性。