索洛經濟增長模型
出自 MBA智库百科(https://wiki.mbalib.com/)
索洛經濟增長模型(Solow Growth Model)
索洛經濟增長模型(Solow Growth Model)是羅伯特·索洛所提出的發展經濟學中著名的模型,又稱作新古典經濟增長模型、外生經濟增長模型,是在新古典經濟學框架內的經濟增長模型。
正當1987年世界股票市場暴跌之時,瑞典皇家科學院宣佈該年度諾貝爾經濟學獎授於一直與里根政府的經濟政策唱反調、主張政府必須有效地干預市場經濟的美國麻省理工學院教授羅伯特·索洛(Robert M·Solow)。許多經濟學界人士認為,紐約股票市場的這場大動蕩,恰恰證實了索洛堅持的理論,使他的經濟增長理論成為當今世界熱門研究課題之一。可是,他的這一理論———表明各種不同因素是如何對經濟增長和發展產生影響的長期經濟增長模型,早在30年前他在一篇題為《對經濟增長理論的貢獻》的論文中就提出來了。[1]
模型的基本假定[1]
索洛在構建他的經濟增長模型時,既汲取了哈羅德—多馬經濟增長模型的優點,又屏棄了後者的那些令人疑惑的假設條件。
索洛認為,哈羅德—多馬模型只不過是一種長期經濟體系中的“刀刃平衡”,其中,儲蓄率、資本—產出比率和勞動力增長率是主要參數。這些參數值若稍有偏離,其結果不是增加失業,就是導致長期通貨彭脹。用哈羅德的話來說,這種“刀刃平衡”是以保證增長率(用Gw表示,它取決於家庭和企業的儲蓄與投資的習慣)和自然增長率(用Gn表示,在技術不變的情況下,它取決於勞動力的增加)的相等來支撐的。
索洛指出,Gw和Gn之間的這種脆弱的平衡,關健在於哈羅德—多馬模型的勞動力不能取代資本,生產中的勞動力與資本比例是固定的假設。倘若放棄這種假設,Gw和Gn之間的“刀刃平衡”也就隨之消失。基於這一思路,索洛建立了一種沒有固定生產比例假設的長期增長模型。
該模型的假設條件包括:
1.只生產一種產品,此產品既可用於消費也可用於投資。
2.產出是一種資本折舊後的凈產出,即該模型考慮資本折舊。
3.規模報酬不變,即生產函數是一階齊次關係式。
4.兩種生產要素(勞動力和資本)按其邊際實物生產力付酬。
6.勞動力永遠是充分就業的。
7.勞動力與資本可相互替代。
8.存在技術進步。
在這些條件下,索洛建立的模型向人們顯示出:在技術繫數可變的情況下,人均資本量具有隨時間推移而向均衡狀態的人均資本量自行調整的傾向(圖一,k1與k2逐漸趨向ko),即,當人均資本量大於其均衡狀態時(k2),人均資本量會有逐漸減小的趨勢,即資本的增加就會比勞動力的增加慢得多;反之,亦然。索洛是人均資本量入手集中分析均衡(即穩定狀態)增長路徑的。
模型的基本框架[1]
索洛把經濟中的全部產出看成僅僅是一種產品的產出。其每年生產量用Y(t)表示,代表社會的實際收入,其中一部分被消費掉,其餘部分用於儲蓄和投資。用於儲蓄的占總產品比例s固定不變,即儲蓄量為sY(t)。K(t)是資本存量。這種資本存量的增加量就是凈投資,即dk/dt或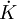 因此,索洛模型的基本方程式可以寫成:
因此,索洛模型的基本方程式可以寫成:
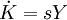 (1)
(1)
因產出是用資本和勞動力生產的,技術能力可用生產函數來反應:
Y=F(K,L) (2)且該函數滿足假設規模報酬不變。
把(2)式代入(1)式,有:
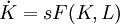 (3)
(3)
其中,L代表勞動力。
由於人口的增長是外生變數,勞動力以一個不變增長率n增加。因此:
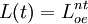 (4)
(4)
索洛把n看成是在沒有技術進步情況下的哈羅德的自然增長率(Gn),把L(t)看成是在t時期可利用的勞動力供給。(4)式的右邊表明勞動力從0期到t期的綜合增長率。我們還可以把(4)式看作是勞動力的供給曲線,“它說的是以指數增長的勞動力完全無彈性地得到就業。勞動力供給曲線是一條縱向線,它隨著勞動力按(4)式的增長而向右移動。於是,調整實際工資率以使全部可利用的勞動力得到雇佣,而邊際生產力等式決定著這種實際上得到控制的工資率”。
把(4)式代入(3)式,索洛給出下列基本方程式:
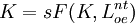 (5)
(5)
他把這個方程式作為在全部可利用的勞動力得到充分利用的情況下決定必須遵循的資本積累的時間軌跡方程式。資本存量和勞動力的時間軌跡一經確知,相應的實際產出的時間軌跡就可根據生產函數計算出來。實際工資率的時間軌跡可用邊際生產力等式確定,即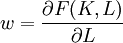 (6)
(6)
索洛把經濟增長過程概括為:“在任何時候,可利用的勞動力供給都由等式(4)給定,而且可利用的資本存量也是一個已知數。既然生產要素的實際報酬可調整而使勞動力和資本得以充分利用,我們就能利用生產函數等式(2)求出當期產出量。於是,儲蓄傾向告訴我們多少凈產出將用於儲蓄和投資,從而我們得知當期的資本凈積累,再加之已積累的存貨,這就為下一期提供了可利用的資本”。
可能的增長類型[1]
上一節的方程式(5)有助於研究資本—勞動力比率(K/L)的行為。為此,索洛引入了一個新的變數r,用來代表資本—勞動力比率,即人均資本量。因此,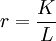 或K=rL。把方程式(4)代入該表達式中,得到:
或K=rL。把方程式(4)代入該表達式中,得到:
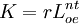 (7)
(7)
把方程式(7)對時間微分,得到資本存量變化率的方程式:
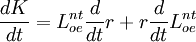
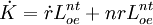
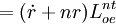 (8)
(8)
把方程式(5)代入方程式(8)中,得到:
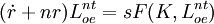 (9)
(9)
方程式(9)表明瞭,在假定勞動力是充分就業的且每一時期的儲蓄是充分就業產出的一個比例s情況下,資本是如何持續增長的。
規模收益不變的假定,意味著生產函數是一階齊次函數。用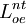 來除方程式(9),得到:
來除方程式(9),得到:
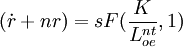 (10)
(10)
方程式(10)的兩邊同時減去nr,得到:
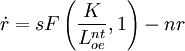
最後,把資本—勞動比率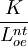 寫成r,得到索洛的基本方程式:
寫成r,得到索洛的基本方程式:
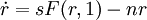 (11)
(11)
其中,r——人均資本存量(K/L)
n——勞動力增長率率(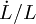 )
)
F(r,1)——人均產出函數或人均收入函數 sF(r,1)——指人均產出中用於儲蓄或投資的產品量 方程式(11)表明,實際用於儲蓄的產品量〔sF(r,1)〕與均衡狀態所需要達到的產品量nr之間的差距,該方程式可以用來找到一條總能達到穩定狀態且與勞動力增長率相一致的資本積累路徑。
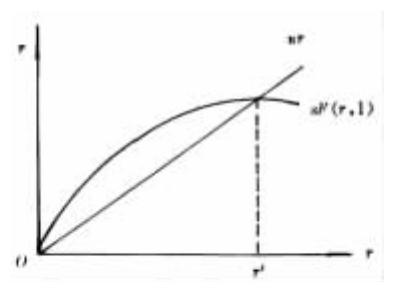
以基本方程式(11)為基礎,索洛用圖示說明瞭可能的增長類型(見圖—1)
在圖—1中,橫軸為人均資本量r,縱軸為人均產出量y,(y=Y/L),通過原點的直線是函數nr,另一條曲線為y=sF(r,1)。
圖—1 可能的增長類型。
代表函數sF(r,1)這樣畫出來的圖示反映出資本的邊際生產力遞減。這兩條曲線在nr=sF(r,1),即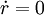 處相交,此時橫坐標為r'當
處相交,此時橫坐標為r'當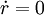 時,人均資本量不變,而且人均資本量增長率與勞動力增長率相等且同為n。資本—勞動力的比率r′一旦確定就不變了,資本和勞動力按該比例增加。倘若規模報酬不變,實際產出也會以相同的相對比率(n)增加,而且每個勞動力的產出將不變。
時,人均資本量不變,而且人均資本量增長率與勞動力增長率相等且同為n。資本—勞動力的比率r′一旦確定就不變了,資本和勞動力按該比例增加。倘若規模報酬不變,實際產出也會以相同的相對比率(n)增加,而且每個勞動力的產出將不變。
如若r′與實際r不一致,資本—勞動力比率情況將如何?若r>r′,則nr>sF(r,1),r將降低以接近於r′;相反,若r<r′,nr<sF(r,1),r將提高以接近於r′。因此,均衡值r′是穩定的。“不管人均資本量的初始值如何,該體系將以自然比率向平衡增長髮展……若初始資本存量低於均衡值,資本和產出將以快於勞動力增長的速度而增加,直至接近均衡值。若該初始比率高於均衡值,資本和產出將以比勞動力增長速度更慢的速度增加。產出的增長總是處於勞動力和資本的增長速度之間”。
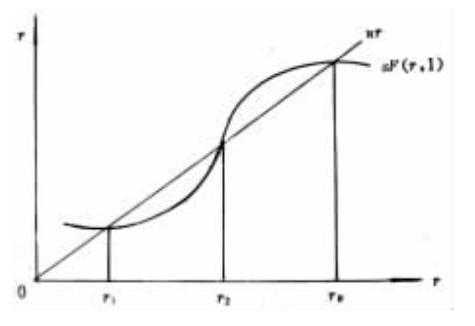
圖—2 生產力曲線。
但是,圖—1所表現出來的那種很強的穩定性並不是絕對的,這取決於生產力曲線sF(r,1)的形狀。在圖—2中,生產力曲線sF(r,1)在r1、r2和r3三處與nr曲線相交。r1和r3是穩定的,而r2則不穩定。“該體系不是按資本—勞動力比率r1進行平衡增長,就是按r3進行平衡增長,這取決於最初可觀察到的資本—勞動比率。在任何一種情況下,勞動力供給、資本存量和實際產出將以比率n漸進增長;但在r1左右,其資本量要比在r3左右為少,故前者的人均產出水平比後者的人均產出水平低。那麼,對於在O和r2之間的初始比率,其相應的平衡增長均衡是r1,而對於大於r2的任何初始比率,其相應的平衡增長均衡就是r3比率r2本身就是一種均衡的但不穩定的增長率,任何偶然的擾動在一定時期內都會被誇大。如此畫出的圖—2使得生產在沒有資本的情況下也要進行”。
索洛對他的長期增長模型作了這樣的總結:“當生產在通常的比例變動和報酬不變的新古典條件下進行時,自然增長率與有保證的增長率之間沒有明確的抵觸是可能的。也許不會有……任何‘刀刃’。該體系能夠調整任何既定的勞動力增長率,最終達到按比例增加的穩定狀態”,即:
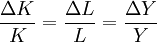
索洛增長模型表明的基本含義[2]
索洛增長模型表明的基本含義是:人均資本擁有量的變化率ḱ取決於人均收入儲蓄率sf(k)和按照既定的資本勞動比配備每一新增長人口所需資本量nk之間的差額。
索洛增長模型sf(k)=ḱ+nk還表明另一個含義。一個社會中的人均儲蓄率sf(k)有兩個用途:
一是用於人均資本擁有量的增加量ḱ,即為每個人配備更多的資本裝備,這被稱作“資本的深化”;
二是用於為每一新增人口提供平均的資本裝備nk,這被稱作“資本的廣化”。換句話說,經濟中的全部儲蓄轉化為投資後,一部分用於提高人均資本擁有量(資本的深化),另一部分則用於為新增人口提供平均數量的資本裝備(資本的廣化)。
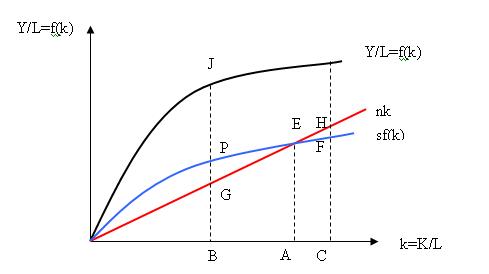
圖中所示,橫軸為人均資本擁有量k,縱軸為人均收入f(k)。集約生產函數曲線f(k)表明人均收入隨著人均資本擁有量的增加而增加,人均產量即人均收入f(k)也相應增加。人均儲蓄曲線sf(k)位於人均收入曲線f(k)的下方,因為儲蓄只是收入的一部分,兩者間的距離為非儲蓄,即消費的部分。
當人均資本擁有量k為OB,則此時的人均收入為BJ,人均儲蓄為BP,這部分人均儲蓄一部分用於裝備每一新增人口即資本廣化的BG和一部分用於人均資本擁有量即資本深化的GP。這意味著k將提高,於是導致f(k)增加,因此,B點將右移到A點。A點資本的深化等於0,全部的人均儲蓄都被用於資本的廣化,經濟達到均衡。反之亦然。
索洛模型的意義與不足[1]
作為創立新古典經濟增長模型的先軀,索洛教授在構造他的長期增長模型過程中,不僅保留了哈羅德—多馬模型的主要特征(如齊次資本函數、比例儲蓄函數以及既定的勞動力增長率),而且還在理論模型的現實性方面有新的突破。主要表現在以下幾個方面:
1.他在分析經濟增長的過程中採用了一種連續性生產函數,從此人們稱其為新古典生產函數。
2.勞動力與資本之間可相互替代的假設使得經濟增長過程具有調整能力,從而該理論模型更接近於現實。
3.長期增長率是由勞動力增加和技術進步決定的,前者不僅指勞動力數量的增加,而且還含有勞動力素質與技術能力的提高,所以,索洛的長期增長模型打破了一直為人們所奉行的“資本積累是經濟增長的最主要的因素”的理論,向人們展示,長期經濟增長除了要有資本以外,更重要的是靠技術的進步、教育和訓練水平的提高。
在一定程度上說,技術進步、勞動力質量的提高比增加資本對經濟增長的作用更大。這種觀點在他30年後獲獎前夕接受採訪時又得到進一步闡述。他說,除了純粹的農業國以外,這一理論對所有國家都適用。“發展中國家不能把本國經濟的發展僅僅依賴於資本和勞動力的增長上。發展中國家,特別是起步較晚國家,要更多地研究如何在現有工業的基礎上逐步提高勞動生產率、技術和教育進程。這樣就能有效地跟上世界經濟的發展”(顧耀銘,1987)許多國家都相繼接受了他的理論,在中高等教育、研究與發展(R&D)等方面,政府不斷增加投資和提供稅收刺激措施,成效顯著。
當然,作為一種理論模式,索洛的長期增長模型也並非盡善盡美。正如森(Sen,1970)教授指出的那樣,索洛的模型也有其不足之處:
1.索洛的增長模型考慮的僅僅是哈羅德的Gw和Gn之間的均衡問題,而忽略了G和Gw之間的均衡。
2.索洛的模型沒有投資函數,此函數一旦引入,哈羅德模型的不穩定性問題即會出現於索洛的模型中。森教授認為,勞動力和資本間的替代性假設似乎並不是新古典學派和新凱恩斯學派對增長研究之不同的關鍵所在,其主要差異在於索洛模型沒有考慮投資函數以及由此產生的企業家對將來預期的重要性。
3.索洛假設要素價格是可變的,這也會給穩定增長的路徑設置障礙。例如,利息率由於流動陷井問題而不會下降到低於一定的最低水平;反過來,這也許使資本—產出比率不能提高到實現均衡增長路徑所必需的水平。
4.索洛模型是以提高勞動生產率的技術進步為假定前提構建的。然而,這一假定只是柯布一道格拉斯生產函數型哈羅德中性技術進步的一個特例,沒有任何經濟證據。
5.索洛增長模型的另一假設是“資本是同質的且易變的”,但事實上,資本品是高度異質的,因此而出現不能簡單加總問題。結果,當存在多種多樣的資本品時,穩定增長路徑是很難實現的。
1.主要結論
(1)無論從任何一點出發,經濟向平衡增長路徑收斂,在平衡增長路徑上,每個變數的增長率都是常數。
(2)在其他外生變數相似的條件下,人均資本低的經濟有更快的人均資本的提高,人均收入低的經濟有更高的增長率。
(3)人均產出(Y/L)的增長來源於人均資本存量和技術進步,但只有技術進步才能夠導致人均產出的永久性增長。
(4)通過調節儲蓄率可以實現人均最優消費和最優資本存量的“黃金律”增長。
(5)儲蓄率的變化只會暫時性地影響增長率,而不會永久性地影響;儲蓄率的顯著變化對平衡增長路徑上的產出變化只有較小的影響,且作用緩慢。
2.批評
(1)未能夠解釋長期經濟增長的真正來源。把技術進步(勞動的有效性)看成為外生給定的,而這恰恰是長期經濟增長的關鍵。因此,索洛模型是通過“假定的增長”來解釋增長的。
(2)理論預測與實際數據不符。如果資本取得的市場收益大致體現了其對產出的貢獻,那麼實物資本積累的變化既不能很好地解釋世界經濟增長,也不能說明國家間的收入差距。
例如:根據C-D生產函數,y = f(k) = ka,一般的a=1/3,設窮國變數帶*,若y/y*=10,則k / k * = 101 / a = 1000。(如此大的資本存量差異!)
資本的邊際產品MPk = f'(k) = aka − 1 = ay(a − 1) / a,若y/y*=10,則MPk / MP * k = 1 / 100。(如此高的資本報酬率差異!)
本条目由以下用户参与贡献
苦行者,蔓草寒烟,funwmy,Kane0135,Lolo,Vulture,Angle Roh,Dan,Cabbage,Zfj3000,鲈鱼,Yixi,贾然,连晓雾,Solitude1314,Gaoshan2013,林巧玲,Llyn.評論(共41條)
非常機械 中國人看不懂中文!
MBA智庫是可以自由參與的百科,如有發現錯誤和不足,可以自由參與編輯和修改。只要通過網頁右上角創建新賬戶,註冊用戶名後即可參與編輯修改,期待您的參與~~
中國人對西方經濟的認識真的好似處於幼兒園水平一樣
全中國就你厲害,就你的認識不是幼兒園水平,那你寫個高水平的讓大家看看啊
這個是以曼昆為代表的新古典巨集觀經濟學模型吧?巴羅的索洛模型與這個有些許不同。不過對於解釋資本存量和國民收入與內生變數的變動關係方面是大同小異的。
其實我沒看懂。。。維基中文解釋的更簡單
果真很簡單。。。
樓上的簡直無語~真是搞笑,什麼翻譯過來的,不好,賣雞蛋的就一定要養雞、就要自己會下蛋?!你看不懂就不好?!講解的很詳細,也挺好的,就是符號最好用經典教材常用的,受眾廣,容易看懂~還有就是配圖隔得遠,要來回拉,思路容易斷,建議改善~總之支持詞條編輯者
索洛模型描述了一個完全競爭的經濟、資本和勞動投入的增長引起產出的增長,而新古典生產函數決定了在勞動供給不變時,資本的邊際產出遞減。這一生產函數與儲蓄率不變,人口增長率不變,技術進步不變的假設結合,形成了一個完整的一般動態均衡模型。
圖片里的數學公式是錯的,請及時糾正! 既然Solow模型是基於新古典生產函數,那麼方程就應該是Y=A*F(K,L)=A*(K^alpha)*L^1-alpha) 從這個方程再推理Y=A*(K^alpha)
The Solow per capita production function The production function model was applied to the study of growth problems by Robert Solow (American economist, Massachusetts Institute of Technology, Nobel prize 1990). Solow began with a production function of the Cobb-Douglas type: Q = A Ka L b where A is multifactor productivity , a and b are less than one, indicating diminishing returns to a single factor, and a + b = 1 , indicating constant returns to scale. Solow noted that any increase in Q could come from one of three sources: 1. an increase in L . However, due to diminishing returns to scale, this would imply a reduction in Q / L or output per worker. 2. an increase in K . An increase in the stock of capital would increase both output and Q / L 3. an increase in A or in multifactor productivity could also increase Q / L or output per worker. To concentrate attention on what happens to Q / L or output per worker (and hence, unless the employment ratio changes, output per capita), Solow rewrote the Cobb-Douglas production function in what we shall refer to as per capita form: Q / L = A K a L b - 1 = A K a / L 1 - b
since multiplying by L b - 1 is the same as dividing by L 1 - b . Also, since we assumed that a + b = 1, a = 1 - b. Q = A K a / L a = A ( K / L ) a Defining q = Q / L and k = K / L, that is, letting small letters equal per capita variables , we have q = A k a
圖片里的數學公式是錯的,請及時糾正! 既然Solow模型是基於新古典生產函數,那麼方程就應該是Y=A*F(K,L)=A*(K^alpha)*L^1-alpha) 從這個方程再推理Y=A*(K^alpha)
上面的公式是Y=A*F(K,L)=(K^alpha)*A*L^1-alpha),而你給的Y=A*F(K,L)=A*(K^alpha)*L^1-alpha)和他是一樣的,只是把A的位置調換,公式沒有錯的












不好!!!