柯布—道格拉斯生產函數
出自 MBA智库百科(https://wiki.mbalib.com/)
柯布-道格拉斯生產函數(Cobb-Douglas production function)
目錄[隱藏] |
柯布—道格拉斯生產函數最初是美國數學家柯布(C.W.Cobb)和經濟學家保羅·道格拉斯(Paul H. Douglas)共同探討投入和產出的關係時創造的生產函數,是以美國數學家C.W.柯布和經濟學家保羅.H.道格拉斯的名字命名的。是在生產函數的一般形式上作出的改進,引入了技術資源這一因素。用來預測國家和地區的工業系統或大企業的生產和分析發展生產的途徑的一種經濟數學模型,簡稱生產函數。是經濟學中使用最廣泛的一種生產函數形式,它在數理經濟學與經濟計量學的研究與應用中都具有重要的地位。它是以美國數學家C·W·柯布和經濟學家保羅·H·道格拉斯的名字命名的。柯布—道格拉斯生產函數的一般形式可以表示為:
他們根據有關歷史資料,研究了從1899-1922年美國的資本和勞動對生產的影響,在技術經濟條件不變的情況下,得出了產出與投入的勞動力及資本的關係。但是柯布-道格拉斯生產函數中把技術水平A作為固定常數,難以反映出因技術進步而給產出帶來的影響。
柯布—道格拉斯生產函數中,如果有任何一種投入品為零,則產出也為零,因此對於生產來說,每種生產要素都是必需的,沒有一種要素可以完全替代另一種要素。
柯布—道格拉斯生產函數是採用的邊際分析方法,可用於分析要素投入對產量(產出)的貢獻率、規模收益和其他系列問題。是生產函數中應用廣泛的一種!
根據研究目的和需要,現在有很多在柯布——道格拉斯生產函數基礎上變形應用的函數形式。
柯布-道格拉斯生產函數的基本形式為:
Y = A(t)LαKβμ
式中Y是工業總產值,At是綜合技術水平,L是投入的勞動力數(單位是萬人或人),K是投入的資本,一般指固定資產凈值(單位是億元或萬元,但必須與勞動力數的單位相對應,如勞動力用萬人作單位,固定資產凈值就用億元作單位),α 是勞動力產出的彈性繫數,β是資本產出的彈性繫數,μ表示隨機干擾的影響,μ≤1。從這個模型看出,決定工業系統發展水平的主要因素是投入的勞動力數、固定資產和綜合技術水平(包括經營管理水平、勞動力素質、引進先進技術等)。根據α 和β的組合情況,它有三種類型:
①α+β>1, 稱為遞增報酬型,表明按現有技術用擴大生產規模來增加產出是有利的。
②α+β<1, 稱為遞減報酬型,表明按現有技術用擴大生產規模來增加產出是得不償失的。
③α+β=1, 稱為不變報酬型,表明生產效率並不會隨著生產規模的擴大而提高,只有提高技術水平,才會提高經濟效益。
美國經濟學家R.M.斯諾提出的中性技術模式即斯諾模型屬於不變報酬型。當μ=1時,斯諾模型為:
Y = A(t)L1 − εKε 或 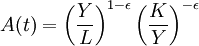
式中(1-ε)是勞動力產出的彈性繫數。根據彈性繫數的經濟意義和數學意義,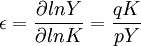 。這裡p是產出價格,q是資本價格。當p=q時,
。這裡p是產出價格,q是資本價格。當p=q時,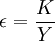 。
。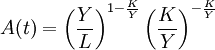 。它表示對生產技術水平、經營管理水平和服務水平的綜合評價,全面反映企業的適應能力、競爭能力和生存能力。A(t)值越大,水平越高。
。它表示對生產技術水平、經營管理水平和服務水平的綜合評價,全面反映企業的適應能力、競爭能力和生存能力。A(t)值越大,水平越高。
根據柯布-道格拉斯生產函數可以得到下列經濟參數(設μ=1):
①勞動力邊際生產力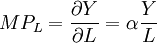 表示在資產不變時增加單位勞動力所增加的產值。
表示在資產不變時增加單位勞動力所增加的產值。
②資產邊際生產力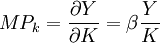 表示在勞動力不變時增加單位資產所增加的產值。
表示在勞動力不變時增加單位資產所增加的產值。
③勞力對資產的邊際代換率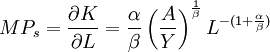 表示產值不變時增加單位勞動力所能減少的資產值。
表示產值不變時增加單位勞動力所能減少的資產值。
④勞動力產出彈性繫數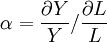 ,表示勞動力投入的變化引起產值的變化的速率。
,表示勞動力投入的變化引起產值的變化的速率。
⑤資產產出彈性繫數 ,表示資產投入的變化引起產值變化的速率。國際上一般取α=0.2~0.4,β=0.8~0.6。中國根據國家計委測算一般可取α=0.2~0.3,β=0.8~0.7。
,表示資產投入的變化引起產值變化的速率。國際上一般取α=0.2~0.4,β=0.8~0.6。中國根據國家計委測算一般可取α=0.2~0.3,β=0.8~0.7。
柯布一道格拉斯生產函數的應用[1]
柯布一道格拉斯生產函數主要用於測定生產過程中資本投人量和勞動投入量對產出量的影響;亦可測定科技進步、資本增長、勞動增長對產出增長的貢獻率。柯布一道格拉斯生產函數為
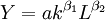
其中:Y代表產出增長率,a代表科技進步率,K代表資本增長率,β1代表資本產出彈性繫數,L代表勞動增長率,β2代表勞動產出彈性繫數。
用柯布一道格拉斯生產函數測定科技進步、資本增長、勞動增長對產出增長的貢獻率,必須先估計參數β1和β2,有下列兩種方法可供選擇。
- 1.正規化法
正規化法是在假定規模報酬不變(β1+β2=1)的條件下,利用產出量、資本量和勞動量三者平均增長率(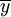 、
、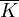 、
、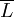 )的比例關係,估計參數a、β1和β2,進而測定科技進步、資本增長、勞動增長對產出增長的貢獻率。計算公式為
)的比例關係,估計參數a、β1和β2,進而測定科技進步、資本增長、勞動增長對產出增長的貢獻率。計算公式為
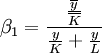
β2 = 1 − β1
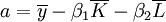
科技進步、資本增長、勞動增長對產出增長的貢獻率的關係式為
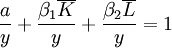
【例1】某企業近10年增加值與資本和勞動投入如圖1所示。根據正規化法估計的科技進步率a=1.9449,資本產出彈性繫數β1=0.5941,勞動產出彈性繫數β2=0.4059,測定的科技進步、資本增長、勞動增長對產出增長的貢獻率分別為24.49%、51.48%和24.03%。為了便於比較,亦可測定不同時期的科技進步、資本增長、勞動增長對產出增長的貢獻率。
- 2.回歸估計法
回歸估計法亦是在假定規模報酬不變(β1+β2=1)的條件下,利用最小二乘法估計參數a、β1和β2,進而測定科技進步、資本增長、勞動增長對產出增長的貢獻率。柯布一道格拉斯生產函數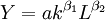 兩邊取對數得:
兩邊取對數得:
lgy=lga+β1lgK+β2lgL
=lga+β1lgK+(1-β1)lgL
lgy-lgL=Iga+β1(lgK-lgL)
lg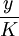 =lga+β1lg
=lga+β1lg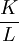
這是一個一元線性回歸模型,可用最小二乘法估計lga和β1,用1-β1求得β2,進而可測定科技進步、資本增長、勞動增長對產出增長的貢獻率。
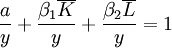
根據表1中所列的數據,用最小二乘法估計的回歸模型為
lg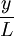 =0.097+0.847 lg
=0.097+0.847 lg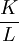
(2.383) (6.562)
R=0.918 F=43.056 SE=0.0990
模型各項檢驗具有顯著性。據此可求得科技進步率a=1.2503,資本產出彈性繫數β1=0.847,勞動產出彈性繫數β2=0.153,測定的科技進步、資本增長、勞動增長對產出增長的貢獻率分別為15.75%、73.39%和9.06%。由於貢獻率之和不等於100%,調整後分別為16.04%、74.74%和9.22%。
- ↑ 龔曙明編著.應用統計學(第二版修訂本).北京交通大學出版社,2007.6.
評論(共25條)
兩個指數說反了。應該是勞動份額占據2/3,資本份額1/3。現代社會是民主社會,以人為本。為了限制兩極分化,達成社會穩定,這也是必須的。
兩個指數說反了。應該是勞動份額占據2/3,資本份額1/3。現代社會是民主社會,以人為本。為了限制兩極分化,達成社會穩定,這也是必須的。
樓上的能說清楚一些麽?看不懂啊~
在美國,勞動收入占據全部收入的2/3,資本收入占據1/3,這個比率長期穩定。這個比率是由於工會爭取高工資的努力與社會儲蓄偏好對收益率要求之間達到的均衡所決定的。所謂cobb-douglas生產函數不過是這個特征的數學體現。
附個案例就好了
已添加了柯布—道格拉斯生產函數的應用部分,望對您有幫助~
這是他們得出的結論
Y = F(N,K) = AN1-θKθ, where Y represents the level of output. (1 - θ) and θ are weights equal to the shares of labor (N) and capital (K) in production, while A is often used as a measure for the level of technology. It can be easily shown that labor and capital each contribute to economic growth by an amount that is equal to their individual growth rates multiplied by their respective share in income.

 无广告阅读
无广告阅读  免验证复制
免验证复制  微信支付
微信支付  支付宝
支付宝  PayPal
PayPal 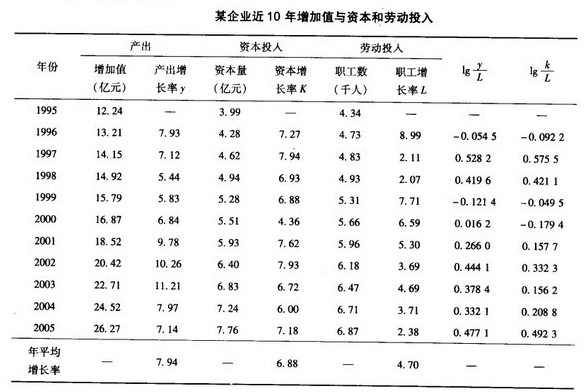











還是不明白