DOE

出自 MBA智库百科(https://wiki.mbalib.com/)

DOE（Design of Experiment,試驗設計）

　　DOE（Design of Experiment）試驗設計，一種安排實驗和分析實驗數據的數理統計方法；試驗設計主要對試驗進行合理安排，以較小的試驗規模(試驗次數)、較短的試驗周期和較低的試驗成本，獲得理想的試驗結果以及得出科學的結論。

　　試驗設計源於1920年代研究育種的科學家Dr.Fisher的研究, Dr. Fisher是大家一致公認的此方法策略的創始者, 但後續努力集其大成, 而使DOE在工業界得以普及且發揚光大者, 則非Dr. Taguchi (田口玄一博士) 莫屬。

• 要為原料選擇最合理的配方時（原料及其含量）；
• 要對生產過程選擇最合理的工藝參數時；
• 要解決那些久經未決的“頑固”品質問題時；
• 要縮短新產品之開發周期時；
• 要提高現有產品的產量和質量時；
• 要為新或現有生產設備或檢測設備選擇最合理的參數時等。

　　另一方面，過程通過數據表現出來的變異，實際上來源於二部分：一部分來源於過程本身的變異，一部分來源於測量過程中產生的變差，如何知道過程表現出來的變異有多接近過程本身真實的變異呢？這就需要進行MSA測量系統分析。

　　試驗設計的三個基本原理是重覆，隨機化，以及區組化。

　　所謂重覆，意思是基本試驗的重覆進行。重覆有兩條重要的性質。第一，允許試驗者得到試驗誤差的一個估計量。這個誤差的估計量成為確定數據的觀察差是否是統計上的試驗差的基本度量單位。第二，如果樣本均值用作為試驗中一個因素的效應的估計量，則重覆允許試驗者求得這一效應的更為精確的估計量。如s₂是數據的方差，而有n次重覆，則樣本均值的方差是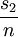。這一點的實際含義是，如果n=1，如果2個處理的y₁ = 145，和y₂ = 147，這時我們可能不能作出2個處理之間有沒有差異的推斷，也就是說，觀察差147-145=2可能是試驗誤差的結果。但如果n合理的大，試驗誤差足夠小，則當我們觀察得y₁隨機化是試驗設計使用統計方法的基石。

　　所謂隨機化，是指試驗材料的分配和試驗的各個試驗進行的次序，都是隨機地確定的。統計方法要求觀察值（或誤差）是獨立分佈的隨機變數。隨機化通常能使這一假定有效。把試驗進行適當的隨機化亦有助於“均勻”可能出現的外來因素的效應。

　　區組化是用來提高試驗的精確度的一種方法。一個區組就是試驗材料的一個部分，相比於試驗材料全體它們本身的性質應該更為類似。區組化牽涉到在每個區組內部對感興趣的試驗條件進行比較。

　　策略一：篩選主要因數（X型問題化成A型問題）

　　實驗成功的標誌：在ANOVA分析中出現了1~4個顯著因數；這些顯著因數的累積貢獻率在70%以上。

　　策略二：找出最佳之生產條件（A型問題化成 T型問題）

　　實驗成功的標誌：在第二階段的實驗中主要的誤差都是隨機因素造成的。

　　因為各因數皆不顯著，因此，每一因數之各項水準均可使用,在此情況下豈不是達到了成本低廉且又容易控制之目的。

　　策略三：證實最佳生產條件有再現性。

　　第一步 確定目標

　　我們通過控製圖、故障分析、因果分析、失效分析、能力分析等工具的運用，或者是直接實際工作的反映，會得出一些關鍵的問題點，它反映了某個指標或參數不能滿足我們的需求，但是針對這樣的問題，我們可能運用一些簡單的方法根本就無法解決，這時候我們可能就會想到試驗設計。對於運用試驗設計解決的問題，我們首先要定義好試驗的目的，也就是解決一個什麼樣的問題，問題給我們帶來了什麼樣的危害，是否有足夠的理由支持試驗設計方法的運作，我們知道試驗設計必須花費較多的資源才能進行，而且對於生產型企業，試驗設計的進行會打亂原有的生產穩定次序，所以確定試驗目的和試驗必要性是首要的任務。隨著試驗目標的確定，我們還必須定義試驗的指標和接受的規格，這樣我們的試驗才有方向和檢驗試驗成功的度量指標。這裡的指標和規格是試驗目的的延伸和具體化，也就是對問題解決的著眼點，指標的達成就能夠意味著問題的解決。

　　第二步 剖析流程

　　關註流程，使我們應該具備的習慣，就像我們的很多企業做水平對比一樣，經常會有一個誤區，就是只講關註點放在利益點上，而忽略了對流程特色的對比，試驗設計的展開同樣必須建立在流程的深層剖析基礎之上。任何一個問題的產生，都有它的原因，事物的好壞、參數的便宜、特性的欠缺等等都有這個特點，而諸多原因一般就存在於產生問題的流程當中。流程的定義非常的關鍵，過短的流程可能會拋棄掉顯著的原因，過長的流程必將導致資源的浪費。我們有很多的方式來展開流程，但有一點必須做到，那就是儘可能詳盡的列出可能的因素，詳盡的因素來自於對每個步驟地詳細分解，確認其輸入和輸出。其實對於流程的剖析和認識，就是改善人員瞭解問題的開始，因為並不是每個人都能掌握好我們所關註的問題。這一步的輸出，使我們的改善人員能夠瞭解問題的可能因素在哪裡，雖然不能確定哪個是重要的，但我們至少確定一個總的方向。

　　第三步 篩選因素

　　流程的充分分析，使我們有了非常寶貴的資料，那就是可能影響我們關註指標的因素，但是到底哪個是重要的呢？我們知道，對一些根本就不或微小影響因素的全面試驗分析，其實就是一種浪費，而且還可能導致試驗的誤差。因此將可能的因素的篩選就有必要性，這時，我們不需要確認交互作用、高階效應等問題，我們的目的是確認哪個因素的影響是顯著的。我們可以使用一些低解析度的兩水平試驗或者專門的篩選試驗來完成這個任務，這時的試驗成本也將最小處理。而且對於這一步任務的完成，我們可以應用一些歷史數據，或者完全可靠的經驗理論分析，來減少我們的試驗因數，當然要註意一點就是，只要對這些數據或分析有很小的懷疑，為了試驗結果的可靠，你可以放棄。篩選因素的結果，使得我們掌握了影響指標的主要因素，這一步尤為關鍵，往往我們在現實中是通過完全的經驗分析得出，甚至抱著可能是的態度。

　　第四步 快速接近

　　我們通過篩選試驗找到了關鍵的因素，同時篩選試驗還包含一些很重要的信息，那就是主要因素對指標的影響趨勢，這是我們必須充分利用的信息，它可以幫助我們快速的找到試驗目的的可能區域，雖然不是很確定，但我們縮小了包圍圈。這時我們一般使用試驗設計中的快速上升（下降）方法，它是根據篩選試驗所揭示的主要因素的影響趨勢來確定一些水平，進行試驗，試驗的目的就像我們在尋找罪犯一樣的縮小嫌疑範圍，我們得出的一個結論就是，我們的改善最優點就在因素的最終反映的水平範圍內，我們離成功更近了一步。

　　第五步 析因試驗

　　在篩選試驗時我們沒有強調因素間的交互作用等的影響，但給出了主要的影響因素，而且快速接近的方法，使我們確定了主要因素的大致取值水平，這時我們就可以進一步的度量因素的主效應、交互作用以及高階效應，這些試驗是在快速接近的水平區間內選取得，所以對於最終的優化有顯著的成效，析因試驗主要選擇各因素構造的幾何體的頂點以及中心點來完成，這樣的試驗構造，可以幫助我們確定對於指標的影響，是否存在交互作用或者那些交互作用，是否存在高階效應或者哪些高階效應，試驗的最終是通過方差分析來檢定這些效應是否顯著，同時對以往的篩選、快速接近試驗也是一個驗證，但我們不宜就在這樣的試驗基礎上就來描述指標與諸主效應的詳細關係，因為對於3個水平點的選取，試驗功效會有不足的可能性。

　　第六步 回歸試驗

　　我們在析因試驗中，確定了所有因素與指標間的主要影響項，但是考慮到功效問題，我們需要進一步的安排一些試驗來最終確定因素的最佳影響水平，這時的試驗只是一個對析因試驗的試驗點的補充，也就是還可以利用析因試驗的試驗數據，只是為了最終能夠優化我們的指標，或者說有效全面的構建因素與水平的相應曲面和等高線，我們增加一些試驗點來完成這個任務。試驗點一般根據回歸試驗的旋轉性來選取，而且它的水平應該根據功效、因數數、中心點數等方面的合理設置，以確保回歸模型的可靠性和有效性。這些試驗的完成，我們就可以分析和建立起因素和指標間的回歸模型，而且可以通過優化的手段來確定最終的因數水平設定。當然為了保險起見，我們最後在得到最佳參數水平組合後進行一些驗證試驗來檢驗我們的結果。

　　第七步 穩健設計

　　我們知道，試驗設計的目的就是希望通過設置我們可以調控的一些關鍵因素來達到控制指標的目的，因為對於指標來講我們是無法直接控制的，試驗設計提供了這種可能和途徑，但是在現實中卻還存在一類這樣的因素，它對指標影響同樣的顯著，但是它很難通過人為的控制來確保其影響最優，這類因素我們一般稱為雜訊因素，它的存在往往會使我們的試驗成果功虧一簣，所以對待它的方法，除了儘量的控制之外可以選用穩健設計的方法，目的是這些因素的影響降低至最小，從而保證指標的高優性能。事實上這些因素是普遍存在的，例如我們的汽車行駛的路面，不可能保證都是在高級公路上，那麼對於一些差的路面，我們怎樣來設計出高性能呢？這時我們會選擇出一些抗干擾的因素來緩解干擾因素的影響，這就是穩健設計的意圖和途徑。通常我們會經常使用在設計和研發階段，但有時也會隨著問題的產生而暴露出來，但我們會提出一個問題了，重新選定主要因素的水平會不會帶來指標的振蕩和劣化，這是完全有可能的，但我們可以通過EVOP等途徑來重新設定以保證因素更改後的輸出效果。

　　註：

　　1.試驗設計需要成本的投入，我們必須確定試驗進行的必要性，以及選取最優的設計方案。

　　2.水平的選取可能直接影響試驗設計的結果，要謹慎的選取，最好有專業知識和歷史數據的支持。

　　3.儘可能的利用一些歷史數據，在確認可靠後提取對我們試驗有用的信息，來儘量減少試驗投資和縮短試驗周期。

　　4.試驗設計並不能提供解決所有問題的途徑，現實當中的局限驗證了這一點，我們要全面考慮解決問題的方式，選取最有效、最經濟的解決途徑。

　　5.註意充分的分析流程，不要遺漏關鍵的因素，不要被一些經驗論的不可能結論左右。

　　6.除了試驗設計涉及的因素外，要儘量確定所有的環境因素是穩定和符合現實的，往往會做不到這一點，我們可以用隨機化、區組化來儘量避免。

　　7.註意結果的驗證和控制，不要輕信結果。

　　8.儘量保證試驗的模擬性，避免一些理想的試驗環境，比如試驗室，理想不現實的環境是的試驗可能根本就沒有作用。

　　9.試驗設計者要關註試驗過程，保證試驗意圖和方案的徹底執行。

　　10.如果實現一步到位的試驗設計是可能的，那就不要猶豫的開展吧，上面的七步只是針對普通的情況。　

　　在工業生產和工程設計中能發揮重要的作用，主要有：

　　1.提高產量；

　　2.減少質量的波動，提高產品質量水準；

　　3.大大縮短新產品試驗周期；

　　4.降低成本；

　　5.試驗設計延長產品壽命。

　　在工農業生產和科學研究中，經常需要做試驗，以求達到預期的目的。例如在工農業生產中希望通過試驗達到高質、優產、低消耗，特別是新產品試驗，未知的東西很多，要通過試驗來摸索工藝條件或配方。如何做試驗，其中大有學問。試驗設計得好，會事半功倍，反之會事倍功半，甚至勞而無功。

　　如果要最有效地進行科學試驗，必須用科學方法來設計。所謂試驗的統計設計，就是設計試驗的過程，使得收集的數據適合於用統計方法分析，得出有效的和客觀的結論。如果想從數據作出有意義的結論，用統計方法作試驗設計是必要的。當問題涉及到受試驗誤差影響的數據時，只有統計方法才是客觀的分析方法。這樣一來，任一試驗問題就存在兩個方面：試驗的設計和數據的統計分析。這兩個是緊密相連的，因為分析方法直接依賴於所用的設計。

　　常見的試驗設計方法，可分為二類，一類是正交試驗設計法，另一類是析因法。

　　（1）正交試驗設計法

　　① 定義

　　正交試驗設計法是研究與處理多因素試驗的一種科學方法。它利用一種規格化的表格——正交表，挑選試驗條件，安排試驗計劃和進行試驗，並通過較少次數的試驗，找出較好的生產條件，即最優或較優的試驗方案。

　　② 用途

　　正交試驗設計主要用於調查複雜系統（產品、過程）的某些特性或多個因素對系統（產品、過程）某些特性的影響，識別系統中更有影響的因素、其影響的大小，以及因素間可能存在的相互關係，以促進產品的設計開發和過程的優化、控制或改進現有的產品（或系統）。

　　案例：^[1]

　　當試驗中只有一個變化的參數時，屬於單因素試驗問題。例如，需要確定液壓作動器的活塞的面積，以使作動器達到最優性能。人們根據對現象的認識，可以估計出最優參數可能存在的區間。如果對它的認識比較清楚，這種估計比較精確，估計的區間較窄；相反，估計的區間就較寬。現在要通過一系列的試驗使認識深化。如果逐步試驗，要使估計區間縮小100倍就需要作100次試驗。但是如果使用區間縮減法中的“黃金分割試驗技術”，只要作11次試驗就可以將區間縮小到百分之一，作14次試驗就可以對區間的認識精度提高500倍。

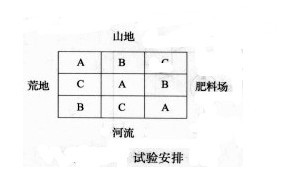
　　在多因素試驗中，往往需要分離出不同因素的影響。譬如要比較A、B、C3種種子的產量。如果只是單純的種子產量問題，似乎只要在3塊同面積的土地上分別用3種種子播種，然後比較產量就可以了。但是如果試驗田的位置在南北方向上處於山地和河流之間，東西方向上處在肥料場和荒地之問，這時仍然任意取3塊等面積的試驗田作試驗，就可能由於土壤的肥脊不同和灌溉的充分與否影響試驗田的產量，而不單是種子一個因素的結果。要估計這些因素的影響，合理的方法是將試驗區分為9塊試驗田(如下圖)，將3種不同的種子的每一種分播在3塊不同的試驗田裡，將3塊田的產量平均，就得到由於種子品種造成的差異(排除了土壤和灌溉的因素)；而將靠肥料場的3塊田的平均產量，與靠荒地的3塊田的平均產量比較，就得到由於土地肥脊程度所造成的產量差異(排除了種子品種和灌溉條件因素)；用靠山的3塊田與傍水的3塊田平均產量進行比較可以看出由於灌溉條件造成的差異(排除了種子品種和土壤條件的差異)。

　　（2）析因法

　　① 定義析

　　析因法又稱析因試驗設計、析因試驗等。它是研究變動著的兩個或多個因素效應的有效方法。許多試驗要求考察兩個或多個變動因素的效應。例如，若幹因素：對產品質量的效應；對某種機器的效應；對某種材料的性能的效應；對某一過程燃燒消耗的效應等等。將所研究的因素按全部因素的所有水平（位級）的一切組合逐次進行試驗，稱為析因試驗，或稱完全析因試驗，簡稱析因法。

　　② 用途

　　用於新產品開發、產品或過程的改進、以及安裝服務，通過較少次數的試驗，找到優質、高產、低耗的因素組合，達到改進的目的。