產量成本法
出自 MBA智库百科(https://wiki.mbalib.com/)
產量法(output method)
目錄 |
產量成本法是根據企業成本的歷史資料,利用成本與產量之間的依存關係來測算產品成本的方法。
產品成本按照其習性,可以分成固定成本和變動成本兩部分。固定成本是成本構成中相對穩定的一部分,產品產量在一定範圍內的變化對其沒有影響,即固定成本不隨產品產量的變化而變化,常常表現為一個常量。變動成本則與產品產量的變化密切相關,產品產量提高,變動成本隨之增高;產品產量降低,變動成本隨之降低。在成本總額中表現為一個變數。根據這種關係可以建立起產品成本的線性方程:
y=a+bx
式中:y—成本總額;
- a—固定成本;
- b—單位變動成本;
- x—產品產量;
- bx—變動成本總額。
變動成本總額隨產量的增減變動而變化。利用歷史資料,運用一定的方法確定a和b的值,預測出任何產量下的產品總成本,即歷史成本法。確定公式中a、b值的方法有高低點法、散佈圖法和回歸分析法等方法。
1、高低點法
高低點法是指從過去一定期間內和相關範圍內的產品產量及產品成本的記錄資料中選出產品產量的最高點和最低點以及產品成本的最高點和最低點,據以推算出單位產品的變動成本b,然後再根據總成本和單位變動成本確定固定成本a來建立成本方程式,確定未來的成本。
高低點法比較簡單,但是由於只依靠兩組數據,所以,選用的數據如不能反映企業生產經營活動的正常情況,計算結果也將存在很大誤差。因此,根據歷史資料採用數學方法計算a和b數值時,應註意進行實際調查研究,考慮預算期影響成本變動的各項因素,對a、b數值進行適當調整,然後根據計劃期產量來計算計劃期的總成本和單位成本。
2、散佈圖法
散佈圖法是根據若幹期歷史資料來繪製各期成本點散佈圖,在各個點之間畫一條反映成本變動平均趨勢的直線,直線的截距為固定成本,然後據此計算單位變動成本,再憑此得到的固定成本、單位變動成本預測計劃期的產品成本的方法。其工作步驟為:
1)收集歷史數據
收集以前各期產量與總成本的歷史數據。
2)畫出散佈圖
將各期總成本數據標入直角坐標系,畫出散佈圖。
3)確定固定成本平均值
根據離散的歷史成本點目測成本隨產量變動的趨勢,畫出一條能反映成本平均變動趨勢的直線,直線與縱軸的交點即固定成本平均值。
4)計算單位變動成本
在直線上任取一點,根據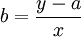 的計算公式,計算出單位變動成本。
的計算公式,計算出單位變動成本。
5)計算總成本
按照計算出的固定成本平均值(a)、單位變動成本(b),預測未來某期產量下的總成本,預測公式為:
y=a+bx
式中:y—未來預測期的總成本;
- x—產量。
3、回歸分析法
回歸分析法是研究變數之間相互關係的一種數理統計方法。它是根據一系列歷史成本資料,用數學上的最小二乘法原理,計算出能代表平均成本水平的直線的截距和斜率,以其作為固定成本和變動成本,進而進行成本預測的方法。
採用回歸分析法,也需要若幹組觀測數據,全部觀測數據通過計算來代替目測,確定出a和b值以及直線議程式,在這一點上與散佈圖法不同。用最小二乘法來確定回歸直線,要求各個觀測點與這條線上相對應點的距離的平方和最小。
依據直線議程式y=a+bx和以前若幹期(n)的歷史資料,可以建立一組決定回歸直線的聯立方程式:
首先,將上述議程式用觀測值的形式來表示,計算公式如下:
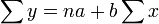
然後,將上式左右兩邊產量進行加權,得出:
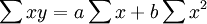
依據以上兩議程式,經過變換,直接列出求a、b值的計算公式。即:
有了a、b值的計算公式後,將其他有關各值代入公式可求得a、b的值,進而得出直線方程。
以上根據回歸直線方程式所計算出來的y值只是一個平均數,這個值只是個近似值,它與實際值存在著一定程度的誤差。誤差愈小,求出的數據愈可靠。誤差的大小決定於回歸直線方程式中y與x之間線性關係的相關程度,相關程度愈高,誤差愈小。通常是利用測定繫數(簡寫為R2)來測定其相關程度,測定繫數愈大說明相關程度愈高,誤差愈小;測定繫數愈小則說明相關程度愈低,誤差愈大。測定繫數的計算公式如下:
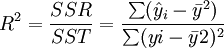
式中:yi——各月份實際產品成本;
-
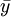 ——實際產品成本的平均數;
——實際產品成本的平均數;
-
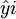 ——回歸直線上的各月成本;
——回歸直線上的各月成本;
- SSR——回歸離差的平方和;
- SST——離差的平方和。
從上列公式可見,回歸離差的平方和在離差的平方和中所占的比例愈大,則得出的R2值就愈大。這說明x、y之間的相關程度愈強,誤差愈小,所求得的直線方程可靠性也愈大。
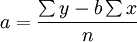
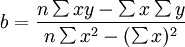








這個東西太好了.很有幫助