产量成本法
出自 MBA智库百科(https://wiki.mbalib.com/)
产量法(output method)
目录 |
产量成本法是根据企业成本的历史资料,利用成本与产量之间的依存关系来测算产品成本的方法。
产品成本按照其习性,可以分成固定成本和变动成本两部分。固定成本是成本构成中相对稳定的一部分,产品产量在一定范围内的变化对其没有影响,即固定成本不随产品产量的变化而变化,常常表现为一个常量。变动成本则与产品产量的变化密切相关,产品产量提高,变动成本随之增高;产品产量降低,变动成本随之降低。在成本总额中表现为一个变量。根据这种关系可以建立起产品成本的线性方程:
y=a+bx
式中:y—成本总额;
- a—固定成本;
- b—单位变动成本;
- x—产品产量;
- bx—变动成本总额。
变动成本总额随产量的增减变动而变化。利用历史资料,运用一定的方法确定a和b的值,预测出任何产量下的产品总成本,即历史成本法。确定公式中a、b值的方法有高低点法、散布图法和回归分析法等方法。
1、高低点法
高低点法是指从过去一定期间内和相关范围内的产品产量及产品成本的记录资料中选出产品产量的最高点和最低点以及产品成本的最高点和最低点,据以推算出单位产品的变动成本b,然后再根据总成本和单位变动成本确定固定成本a来建立成本方程式,确定未来的成本。
高低点法比较简单,但是由于只依靠两组数据,所以,选用的数据如不能反映企业生产经营活动的正常情况,计算结果也将存在很大误差。因此,根据历史资料采用数学方法计算a和b数值时,应注意进行实际调查研究,考虑预算期影响成本变动的各项因素,对a、b数值进行适当调整,然后根据计划期产量来计算计划期的总成本和单位成本。
2、散布图法
散布图法是根据若干期历史资料来绘制各期成本点散布图,在各个点之间画一条反映成本变动平均趋势的直线,直线的截距为固定成本,然后据此计算单位变动成本,再凭此得到的固定成本、单位变动成本预测计划期的产品成本的方法。其工作步骤为:
1)收集历史数据
收集以前各期产量与总成本的历史数据。
2)画出散布图
将各期总成本数据标入直角坐标系,画出散布图。
3)确定固定成本平均值
根据离散的历史成本点目测成本随产量变动的趋势,画出一条能反映成本平均变动趋势的直线,直线与纵轴的交点即固定成本平均值。
4)计算单位变动成本
在直线上任取一点,根据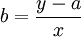 的计算公式,计算出单位变动成本。
的计算公式,计算出单位变动成本。
5)计算总成本
按照计算出的固定成本平均值(a)、单位变动成本(b),预测未来某期产量下的总成本,预测公式为:
y=a+bx
式中:y—未来预测期的总成本;
- x—产量。
3、回归分析法
回归分析法是研究变量之间相互关系的一种数理统计方法。它是根据一系列历史成本资料,用数学上的最小二乘法原理,计算出能代表平均成本水平的直线的截距和斜率,以其作为固定成本和变动成本,进而进行成本预测的方法。
采用回归分析法,也需要若干组观测数据,全部观测数据通过计算来代替目测,确定出a和b值以及直线议程式,在这一点上与散布图法不同。用最小二乘法来确定回归直线,要求各个观测点与这条线上相对应点的距离的平方和最小。
依据直线议程式y=a+bx和以前若干期(n)的历史资料,可以建立一组决定回归直线的联立方程式:
首先,将上述议程式用观测值的形式来表示,计算公式如下:
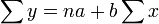
然后,将上式左右两边产量进行加权,得出:
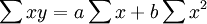
依据以上两议程式,经过变换,直接列出求a、b值的计算公式。即:
有了a、b值的计算公式后,将其他有关各值代入公式可求得a、b的值,进而得出直线方程。
以上根据回归直线方程式所计算出来的y值只是一个平均数,这个值只是个近似值,它与实际值存在着一定程度的误差。误差愈小,求出的数据愈可靠。误差的大小决定于回归直线方程式中y与x之间线性关系的相关程度,相关程度愈高,误差愈小。通常是利用测定系数(简写为R2)来测定其相关程度,测定系数愈大说明相关程度愈高,误差愈小;测定系数愈小则说明相关程度愈低,误差愈大。测定系数的计算公式如下:
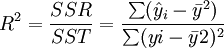
式中:yi——各月份实际产品成本;
-
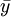 ——实际产品成本的平均数;
——实际产品成本的平均数;
-
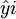 ——回归直线上的各月成本;
——回归直线上的各月成本;
- SSR——回归离差的平方和;
- SST——离差的平方和。
从上列公式可见,回归离差的平方和在离差的平方和中所占的比例愈大,则得出的R2值就愈大。这说明x、y之间的相关程度愈强,误差愈小,所求得的直线方程可靠性也愈大。
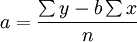
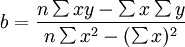








这个东西太好了.很有帮助