產業經濟場

用手机看条目

出自 MBA智库百科(https://wiki.mbalib.com/)

什麼是產業經濟場

　　物理學對“場”的認識已較為明確，即場是物質存在的一種基本形式，具有能量、動量和質量，具體可把場定義為物理量在空間或部分空間的分佈。產業經濟場的提出是受物理學場論的啟示，將產業與電荷或粒子作類比產生的概念。我們認為產業經濟場是產業對其周圍作用的經濟場空間，即由於產業存在或狀態改變所引起的經濟影響因數分佈不均勻產生系統態勢的時空範圍。

　　產業經濟場的質量主要包含產品的物質材料、生產技術、資金投入、設備能力、產品功能、經營管理、售後服務等直接和間接投入量。產業經濟場的能量是以產品服務滿足於社會需要的能力，即質量與數量的綜合作用力。它不是一種物理量，而是一種社會經濟活動量。產業經濟場的動量是產品交換所代表的利益關係，通常與產業經濟場的質量及耗費時間密切相關。產品的流向、流速和流量以及對產品的設計、生產、銷售價格和方式的定位均決定著產業經濟場的動量。

[編輯]

產業經濟場的特征

　　(1)產業經濟場的客觀實在性。

　　確定產業經濟場的客觀實在性是進一步研究經濟場理論的基礎。儘管產業經濟場並不像產業實體那樣有形有質、可觸可摸，但其客觀存在是毋庸置疑的。產業經濟場是由經濟影響因數場組成的，而作為經濟影響因數的物質材料、生產技術、資金投人、設備能力、產品功能以至產業本身是客觀存在的。產業經濟場儘管並非這些物質性因數本身，而是受產業存在或存在狀態改變作用而產生的量變。但是不能否認這些影響因數量變部分的物質性。因此，理論上產業經濟場具有客觀物質性。

　　(2)產業經濟場的混沌性。

　　如果說產業經濟場的客觀實在性是研究產業經濟場的物質基礎，那麼產業經濟場的混沌性就是研究經濟場的理論前提。產業經濟場的混沌性具有以下幾方面含義:首先，產業經濟場的混沌性表現為周期性與非周期性的辯證統一。由於產業經濟場受產業變化的影響，而產業變化恰恰是周期性與隨機性的矛盾統一體，相應地產業經濟場也就處於周期性和非周期性的辯證統一之中。其次，產業經濟場的混沌性具有自相似性。所謂自相似性是指一個對象能在一定範圍內局部放大再現其總體結構性質。產業經濟場的這一特性使得運用局部—整體法研究產業經濟場成為可能。最後，產業經濟場的混沌性還表現在混沌中包含有序現象，低層次混沌往往是高層次有序的基礎。沒有混沌就不會出現結構的有序化。

　　(3)產業經濟場的恆變性。

　　產業經濟場的多種客觀屬性是時刻變化的，這是由於各個經濟影響因數無時無刻不受產業系統內產業的互動作用而發生變化，而變化的產業經濟場又驅使產業不斷調整自身狀態。兩方面相互作用即導致產業經濟場的恆變與動態平衡。產業經濟場的恆變性還體現在經濟發展的周期性波動方面。認識了經濟場的波動性及其規律，我們便可以更好地在現實經濟生活中運用這一規律，減少經濟波動的影響，使經濟更好、更快地發展。

　　(4)產業經濟場的彌散性和疊加性。

　　根據經濟場理論，產業經濟場不以點狀存在，亦不以線狀存在。產業經濟場產生於產業周圍，呈現彌散狀態充溢於整個產業系統之中。在產業系統中的任一時空坐標，都存在著系統內的任一產業經濟場。產業經濟場並非孤立存在，許多場以系統形式位於同一時空位置並產生疊加場效應。產業系統中任一時空坐標的產業都受到相關產業及周圍環境在該點的疊加作用。產業經濟場的彌散性和疊加性是產業間相互作用的根源。正是由於產業經濟場的彌散和疊加，任兩個產業相隔一定空間距離時就會發生作用，當產業間距離很大時，作用變弱;當距離縮短時，作用變強。產業經濟場的疊加方式是複雜的，一般來說是非線性疊加，並常常存在消減性疊加的情況。

　　(5)產業經濟場的可感知性。

　　產業經濟場的彌散疊加是產業經濟場發生作用的物質基礎。產業的一切活動都是由外部信息和內部運作決定的。產業經濟場要令產業對之發生響應就必須能被產業通過某些形式感知。產業根據對產業經濟場的感知(信息輸入)作出相應的適應性對策(信息處理)，而後調整自身的行為、位置等存在狀態(信息反饋)。特定產業並不能感知產業經濟場的一切信息，同時對產業經濟場的感知方式、靈敏度等也存在不同程度的產業間差異，因此產業對同樣的產業經濟場就會有不同反應。這就是產業經濟場疊加不完全的原因。

[編輯]

產業經濟場的運行規律^[1]

　　在愛因斯坦引力場理論中，時空彎曲表明引力場存在，物質粒子按黎曼空間短程線運動;在電磁場理論中，電磁場運動規律體現在麥克斯韋方程組中，帶電粒子按明可夫斯基空間短程線運動，即物理學中物質場按自身固有規律運動。產業經濟場亦存在其自身固有規律，處於產業經濟場中的經濟活動均被納人其運行軌道之中。與物質場運行規律相似，產業經濟場也是以橢圓規律運行的。經濟學家帕烏斯、範·格爾德倫和德·沃爾夫發現的經濟長波，而熊彼特又使我們明白經濟波動中的基欽周期、尤格拉周期和康德拉捷夫周期。由此，我們又可得到:產業經濟場是以波動性規律運行的。可見，產業經濟場既以橢園性規律運行，又以波動性規律運行。根據泛複變函數理論，橢圓性運動與數學上的黎曼空間構成對應關係，波動性運動與數學上的雙曲空間構成對應關係。這裡可以把黎曼空間和雙曲空間統一稱為XS空間。則產業經濟場是以XS空間方式運行的。

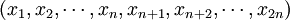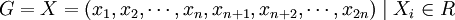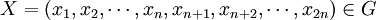　　設2n個有序實數 $(x_1 , x_2 , \cdots , x_n , x_{n+1} , x_{n+2} , \cdots , x_{2n})$ 的全體構成的集合為: $G = {X = (x_1 , x_2 , \cdots , x_n , x_{n+1} , x_{n+2} , \cdots , x_{2n}) \mid X_i \in R}$ 對任意 $X = (x_1 , x_2 , \cdots , x_n , x_{n+1} , x_{n+2} , \cdots , x_{2n}) \in G$ ，令

　　 $λ 1 = x 1 + x n + 1$ 　　　　 $μ 1 = μ 1 - μ n + 1$

　　 $λ 2 = x 2 + x n + 2$ 　　　　 $μ 2 = μ 2 - μ n + 2$

　　 $\cdots$ 　　　　 $\cdots$ 　　　　 $\cdots$ 　　　　　　 $\cdots$

　　 $λ n = x n + x 2 n$ 　　　　 $μ n = μ n - μ 2 n$

　　記 $λ = (λ 1,λ 2,λ n),μ = (μ 1,μ 2,μ n)$ ，則x與 $(λ,μ n)$ 表示G中的同一點，記為 $x ˜(λ,μ n)$ 。泛複變函數理論指出，G中任意兩鄰近點間廣義距離ds定義為

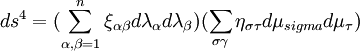　　 $ds^4 = (\sum_{\alpha , \beta = 1}^n \xi_{\alpha \beta} d \lambda_{\alpha} d \lambda_{\beta})(\sum_{\sigma \gamma} \eta_{\sigma \tau} d \mu_{sigma} d \mu_{\tau})$ (3)

　　其中， $ξ αβ = ξ αβ (λ 1,λ 2,λ n)$

　　　　　　 $η στ = η στ (μ 1,μ 2,μ n)$ 　　　　(4)成為G的度規，且 $ξ αβ = ξ αβ$ ， $η στ = ητσ$

　　我們把定義了廣義距離ds空間G稱為XS空間。稱

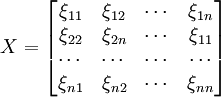
　　 $\Chi = \begin{bmatrix} \xi_{11} & \xi_{12} & \cdots & \xi_{1n} \\ \xi_{22} & \xi_{2n} & \cdots & \xi_{11} \\ \cdots & \cdots & \cdots & \cdots \\\xi_{n1} & \xi_{n2} & \cdots & \xi_{nn} \end{bmatrix}$

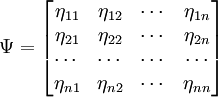　　 $\Psi = \begin{bmatrix} \eta_{11} & \eta_{12} & \cdots & \eta_{1n} \\ \eta_{21} & \eta_{22} & \cdots & \eta_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ \eta_{n1} & \eta_{n2} & \cdots & \eta_{nn} \end{bmatrix}$ 為廣義距離ds的度規矩陣。若以 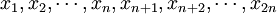$x_1 , x_2 , \cdots , x_n , x_{n+1} , x_{n+2} , \cdots , x_{2n}$ 表示經濟影響因數，比如產業的供給、需求、價格、投人和產出等，則 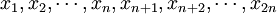$x_1 , x_2 , \cdots , x_n , x_{n+1} , x_{n+2} , \cdots , x_{2n}$ 不僅成為描述XS空間的坐標系統，而且同時也能夠描述產業經濟場。因為產業經濟場與XS空間G構成對應關係，根據泛複變函數理論可知XS空間G的結構和性質完全由度規( $(ξ αβ,η στ)$ 決定。因此，我們認為度規 $(ξ αβ,η στ)$ 不僅決定了XS空間G的結構和性質，同時也決定了產業經濟場。由於經濟場的存在，XS空間是彎曲的，所以描述經濟場的坐標系統是曲線坐標系統。

　　根據XS空間相量場基本理論可以求出表徵產業經濟場度規 $(ξ αβ,η στ)$ 所滿足的場方程:

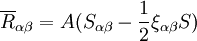
　　 $\overline R_{\alpha \beta} = A(S_{\alpha \beta} - \frac{1}{2} \xi_{\alpha \beta} S)$

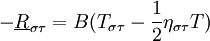　　 $- \underline R_{\sigma \tau} = B(T_{\sigma \tau} - \frac{1}{2} \eta_{\sigma \tau} T)$ 　　　　(6)

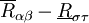　　式中: $\overline R_{\alpha \beta} - \underline R_{\sigma \tau}$ 為XS空間G的“曲率”相量，A,B是表徵產業經濟特特性的常量，(S_{\alpha \beta} , T_{\sigma \tau})是產業經濟場的能量相量，且 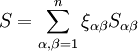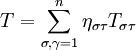$S = \sum_{\alpha , \beta = 1}^n \xi_{\alpha \beta} S_{\alpha \beta}$ ， $T = \sum_{\sigma , \gamma = 1} ^n \eta_{\sigma \tau} T_{\sigma \tau}$ 。這裡，我們只需知道表徵產業經濟場特性的常量A,B和產業經濟場的能量分佈 $(S αβ, T στ)$ ，就可以根據場方程(6)解出度規 $(ξ αβ,η στ)$ ，從而得到該產業的運行規律。改革開放以來，我國建立了許多高新技術產業開發區並給予了許多優惠政策，就是為了增強區域產業發展的經濟能量分佈，由場方程(6)解出的度規 $(ξ αβ,η στ)$ 能夠表徵出較強的產業經濟場。