兩階段增長模型
出自 MBA智库百科(https://wiki.mbalib.com/)
兩階段增長模型(Two-Stage Growth Model)
目錄 |
兩階段增長模型(Two Stage Growth Model)就是假設企業增長呈現兩個階段:第一階段為超常增長階段,又稱為觀測期,其增長率高於永續增長率,實務中的預測期一般為5~7年;第二階段是永續增長階段,又稱永續期,增長率為正常穩定的增長率。對達到穩定期前的預測期長度的估計非常重要。通常假設預測期為一個不穩定的發展期,即投資資本回報率與資本成本不相等。但長久的競爭最終使投資報酬率等於其資本成本,也就是最終會達到穩定期,因此預測期的長短會間接影響企業價值的大小。因此有必要根據行業的發展狀況與公司的競爭戰略地位估計公司的預測期長度。
該模型對企業股權價值計算的核心是正確區分觀察期和永續期,並正確計算兩個階段的現金流量和折現繫數。判斷企業是否進入永續增長狀態的標誌有兩個:第一,在永續增長狀態下,企業具有穩定的銷售增長率,其大約等於巨集觀經濟的名義增長率;第二,企業具有穩定的投資資本回報率,並與資本成本接近。
兩階段增長模型的框架[1]
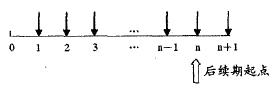
假設企業第n年現金流量增長率為g,n+1年以後增長率均為g,則對企業兩個階段時間間隔的劃分成為計算其現金流量的關鍵點。2005年與2006年全國註冊會計師《財務成本管理》輔導教材在實例分析中對兩種情況下後續期的起點作出了不同的處理。2005年規定後續期起點為第n年,2006年無論課本或習題則統一更正為第n+1年,這不禁會使讀者產生困惑。為了驗證兩種方法的正確性,擬對兩種方法進行推導演算。
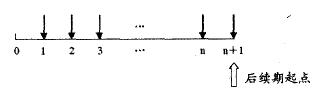
將永續期起點視為第n+1年,其現金流量圖可以表示如下:
則企業的股權價值V為:
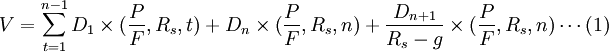
將永續期起點視為第n年,其現金流量圖可以表示如下:
則企業股權價值V為:
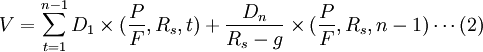
比較以上兩種計算方法發現,n-1年以前的價值在兩種方法下計算結果相同,其區別在於對第n年以後的現值的計算。對公式(2)中後半部分進行推導得出:

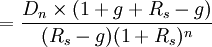
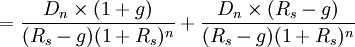
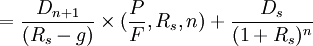
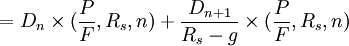
將式(3)帶入公式(2),替換公式(2)的後半部分,則可以得出:公式(1)=公式(2)。
從以上計算結果可以看出,在企業第n年增長率與後續期增長率相同的情況下,無論將第n年還是第n+1年作為企業計算股權價值的後續期起點,其計算結果都完全一致。同樣,這種結論也適合於企業實體現金流量的“兩階段增長”模型。
兩階段增長模型的模式[2]
模式一:第一階段為股利超常增長階段,股利增長率較高且不變,第二階段為股利穩定增長階段,股利增長率較低且預計長期穩定。這一模式稱為“恆恆模式”。
這種模式對應於這樣一類公司,其在發展的第一階段,由於可供再投資的凈現值為正的項目較多,留置盈利較多,股利派發率較低,但這些盈利的項目使得公司盈利和股利的增長率較高且不變。當公司發展進入第二階段後,由於市場競爭趨於白熱化,可供再投資的盈利機會越來越少,留置盈利較少,公司就會提高股利派發率,公司盈利能力的下降就會使得盈利和股利的增長率都下降到一個穩定水平。股利派發率的定義式為:
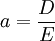
其中a為dividend payout ratio,即股利派發率。D為dividend per share,即每股股利。E為earnings per share,即每股盈利。
模式二:第一階段為股利超常增長階段,且股利增長率不變。第二階段為股利零增長階段,股利長期穩定。這一模式稱為“恆零模式”。這種模式對應於這樣一類公司,其發展的第一階段與第一種模式的公司類似,其發展的第二階段,由於市場高度飽和,可供再投資的盈利機會基本沒有,因而公司不留置任何盈利,把股利派發率提高到1OO ,盈利和股利的增長率都降為零。
模式三:第一階段為股利零增長階段,第二階段為股利穩定增長階段,股利增長率長期穩定。這種模式稱為“零恆模式”。這種模式對應於這樣一類公司,其發展的第一階段有較多的再投資盈利機會,公司留置較多盈利,因而股利金額較少,保持不變,即增長率為零。這樣盈利增長較快,而股利派發率經常向下變動,以保持一個較少而穩定的股利金額。當公司進入發展的第二階段之後,由於本行業趨於飽和,再投資的盈利機會越來越少,因而公司減少留置盈利,把股利派發率提高到一個穩定的較高水平,盈利和股利都保持一個長期穩定的增長率。
模式四:第一階段為零股利階段,第二階段為股利穩定增長階段,股利增長率長期穩定[3](p2 ∞’。這一模式稱為“無恆模式”。 .這種模式對應於這樣一類公司,其發展的第一階段有很多可供再投資的凈現值為正的項目機會,因而不派發股利。當公司進入發展的第二階段之後,由於再投資的盈利機會越來越少,公司把股利派發率提高到一個穩定水平,盈利和股利保持一個較低的長期穩定增長率。
模式五:第一階段為零股利階段,第二階段為股利零增長階段,股利增長率為零。這一模式稱為“無零模式”。
這種模式對應於這樣一類公司,其發展的第一階段公司有很多再投資的盈利機會,因而不派發股利。當公司發展進入第二階段後,由於市場飽和,已基本沒有再投資項目機會,因而把股利派發率提高到100 ,股利增長率為零。
兩階段增長模型的應用局限[1]
(一)理論假設存在局限性
該模型假設企業現金流量的增長呈現出兩階段態勢。這種假設在實務中只是一種近似正確的假設,企業的發展不可能在每個會計年度都完全符合兩階段的假設。因此該模型只能近似估計企業的股權或實體價值
(二)未來現金流量難以確定
“兩階段增長”模型作為現金流量折現法的一種應用,因而帶有現金流量折現法的一些缺陷。現金流量折現法的核心思想是將企業未來預期的現金流量按一定的折現率進行貼現,將其折算為現值以評價公司價值。這種方法需要預測公司各項已投資項目以及公司整體的未來凈現金流量,然後根據一定的折現率計算出投資項目的現值,也就是公司的價值。然而由於巨集觀經濟未來的不確定性以及經營環境的複雜多變性,導致了投資項目未來收益的不確定性,投資的現金流從本質上說是不確定的,一般而言,決策者很難準確估計某個投資項目在其壽命期內的凈現金流量。很顯然,由於企業未來的現金流量難以或者無法得到準確的預測,因而這種方法存在著難以彌補的缺陷。
(三)折現率的確定存在問題
目前的評估方法中,折現率一般是在企業資金成本的基礎上,綜合考慮企業的財務風險因素而選取的。在具體評估企業價值時,一般會以靜止的方法確定折現率,以目前資本結構下的折現率進行企業價值評估,折現率是固定的。但是在實踐中,由於企業經營活動不斷變化,致使企業風險也在不斷變化,進而影響到資本結構中各種資金的權重,導致折現率波動,從而引起企業價值評估結果變化。
綜上所述,“兩階段增長”模型帶有較強的主觀陛。無論其假設條件、未來現金流量或者其折現率的估算都帶有主觀色彩。儘管“兩階段增長”模型存在諸多局限性,但是這種模型仍然具有一定的科學性,在實踐中也初步顯示出其優越性,因而受到國內外許多專家學者的關註,並且為世界許多先進企業所接受及應用。我們必須清楚其適用性,在理論與實務中不斷促進其逐步完善。
運用該模型進行股權估價時,同樣必須註意模型中的約束條件。穩定增長模型所要求的增長率約束條件或假設在兩階段增長模型中依然必須具備。除此之外,如何判斷高速增長?如何劃分高速增長階段與穩定增長階段?這也是實際工作中較難以把握的事實。特別是公司的高速增長時期的紅利增長率與穩定增長時期的紅利增長率存在明顯的不同,由此引致股權要求的收益率相應地不同,從而分析人員在兩階段模型中能否合理地使用不同階段所要求的股權收益率,直接關係到估價的有效性。'
兩階段模型一般適合於具有這樣特征的公司:公司當前處於高速增長階段,並預期今後一段時期內仍保持這一較高的增長率,在此之後,支持高速增長率的因素消失。如,模型適應於一種情形是:某公司擁有一種在未來幾年內能夠產生出色盈利的產品專利權,在這段時間內,預期公司將實現超常增長,一旦專利到期,預計公司無法保持超常的增長率,從而進入穩定增長階段。另一種情形是:一家公司處於一個超常增長的行業,而這個行業之所以能夠超常增長,是因為存在很高的進入壁壘(國家政策、基礎設施所限),並預計這一進入壁壘在今後幾年內能夠繼續阻止新的進入者進入該行業。當然,我們在使用兩階段增長模型時,對兩階段間增長率的過度懸殊不能過大,要適中。如果公司運營從一個高速增長階段陡然下降到穩定增長階段,用這種模型進行估價其結果不太合理。








幾家上市公司能永續?