現金流量圖

出自 MBA智库百科(https://wiki.mbalib.com/)

現金流量圖（Cash flow diagram）

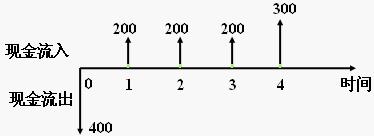
　　現金流量圖是一種反映經濟系統資金運動狀態的圖式，即把經濟系統的現金流量繪入一時間坐標圖中，表示出各現金流入、流出與相應時間的對應關係。運用現金流量圖，就可全面、形象、直觀地表達經濟系統的資金運動狀態。

　　現金流量圖是描述現金流量作為時間函數的圖形，它能表示資金在不同時間點流入與流出的情況。它是經濟分析的有效工具，其重要有如力學計算中的結構力學圖。

　　現金流量圖包括三大要素：大小、流向、時間點。

　　其中：大小表示資金的數額；流向指項目的現金流入或流出；時間點是指現金流入或現金流出所發生的時間。

　　1、橫軸表示時間軸，將橫軸分為n等份，註意第n-1期終點和第n期的始點是重合的。每一等分代表一個時間單位，可以是年、半年、季、月或天。

　　2、與橫軸垂直向下的箭頭代表現金流出，與橫軸垂直向上的箭頭代表現金流入，箭頭的長短與金額的大小成比例。

　　3、代表現金流量的箭頭與時間軸的焦點即表示該現金流量發生的時間。

　　由此可知，要正確繪製現金流量圖，必須把握好現金流量的三要素，即現金流量的大小、方向、時間點。

　　現金流量圖與立腳點有關，從借款人角度出發和從貸款人角度出發所繪現金流量圖不同。

　　說明：

　　1、水平線是時間標度，時間的推移是自左向右， 每一格代表一個時間單位（年、月、日）；時間長度稱為期數。

　　2、垂直箭線表示現金流量：常見的向上——現金的流入，向下——現金的流出。

　　3、一般假定現金的支付都發生在每期期末。

　　4、現金流量圖與立腳點有關。

　　註意：

　　1、時間的連續性決定了坐標軸上的每一個時點既表示上一期期末也表示下一期期初，如第一年年末的時刻點同時也表示第二年年初。

　　2、立腳點不同，畫法剛好相反。

　　3、凈現金流量 = 現金流入－現金流出

　　4、現金流量只計算現金收支(包括現鈔、轉帳支票等憑證)，不計算項目內部的現金轉移(如折舊等)。

　　應有明確的發生時點；必須實際發生（如應收或應付賬款就不是現金流量）；不同的角度有不同的結果（如稅收，從企業角度是現金流出；從國家角度都不是）。

　　一、現金流量圖的畫法

　　現金流量圖是一種反映經濟系統資金運動狀態的圖式，即把經濟系統的現金流量繪入一時間坐標圖中，表示出各現金流入、流出與相應時間的對應關係。運用現金流量圖，就可全面、形象、直觀地表達經濟系統的資金運動狀態。

　　它是在課程講授和題目分析中使用，主要用於分析現金流量發生的時間點、大小、方向，確定其形式，並選擇所使用的公式。

　　因為在需要分析現金流鼉的案例中，現金流量的時間點、大小和方向是最主要的三個因素，而且所涉及的因素和數據較多，有時候會涉及到納稅的計算、利息支出等，在分析中容易出現遺漏或錯誤。而使用現金流量圖更為直觀，不容易遺漏數據。

　　具體畫法如下：

　　1.因為涉及到時間點的問題，我們在分析時，必須使用坐標圖。以橫軸為時間軸，向右延伸表示時間的延續，根據題目中涉及的期間劃分成若幹個時間單位，軸上每一刻度表示一個時間單位，可取年、半年、季或月等，由左至右分別為起始日和終止日，時間單位分別標記為0、1、2……N，零表示時間序列的起點。

　　根據題目中的資金流動，分析每一筆資金流動的時點。

　　2.相對於時間坐標的垂直箭線代表不同時點的現金流量情況。一般情況下，在橫軸上方的箭線表示現金流入，即表示收益；在橫軸下方的箭線表示現金流出，即表示費用。

　　3.箭頭的長短表示現金的多少，在各箭線上方(或下方)註明現金流量的具體數值。

　　4.箭線與時間軸的交點即為現金流量發生的時間點，這對於分析現金流量的形式，選擇使用公式有重要意義。

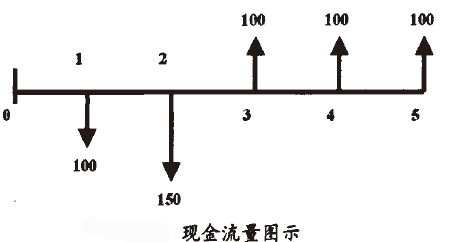
　　例如：某企業計劃投資的一個項目，在第一年年末需要投資100萬元，第二年年末需要投資150萬，項目能在以後三年內每年年末產生100萬的收入，如果資金成本為12％，試計算該項目是否值得投資?經過分析可以繪製出現金流量圖如下圖所示。通過對這個現金流量圖的分析，我們可以發現，兩次現金流出的金額是不相等的，只能使用複利現值的公式分兩步計算現金流出的現值。而三次現金流入的金額是相等的，是一個遞延年金的形式，期數為3，而遞延期為2，就可以直接使用公式計算了。

　　總之，要正確繪製現金流量圖，必須把握好現金流量的三要素，即：現金流量的大小(現金數額)、方向(現金流入或流出)和作用點(現金髮生的時間點)。

　　二、現金流量圖在教學中的應用

　　1、一般應用

　　在計算項目投資的時間價值時，現金流量的分析是最困難的，我們以一個簡單的例題來說明現金流量圖的使用。當然在實際的工作或者考試中碰到的問題要複雜的多。

　　例：某個項目投資總額1000萬元，分5年支付工程款，3年後開始投產，有效期限為5年。投產開始時墊付流動資金200萬元，結束時收回。投產後每年可產生300萬元的現金流入。假設資金成本為10%，試用凈現值法分析該項目是否可行?要計算這個題目，必須先分析現金流量，我們以現金流量圖來進行分析。為了更加清楚，我們用兩個圖形分別表示現金流出和現金流入。

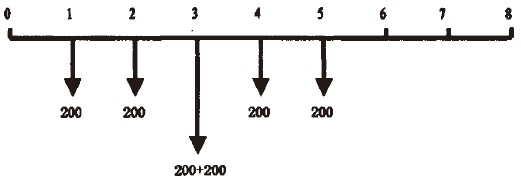
　　該項目的現金流出情況如下圖所示：

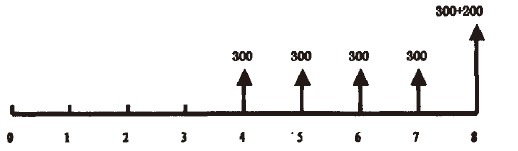
　　上圖可分解為A=200，n=5的普通年金和S=200，n=3的複利該項目的現金流人情況如下圖所示：

　　上圖可分解為A=300，n=8，m=3的遞延年金和5=200，n=8的複利。

　　通過這兩個圖形可以看出，現金流出量有兩組數據需要計算：一個是A=200，n=5的普通年金現值，一個是S=200，n=3的複利現值；現金流入量也有兩組數據需要計算：一個是A=300，n=8，m=3的遞延年金現值。一個是S=200，n=8的複利現值。瞭解了這些就可以直接將數據代入相關的公式計算結果了。

　　2。特殊用法

　　在很多時候，分析項目的現金流量需要做一些變形，才能套用公式，可以大大減少計算量。主要形式有預付年金和遞延年金轉化為普通年金，然後用普通年金的計算方法來計算。在實際應用中，還有很多情況，需要根據題目的要求來具體分析，這裡只用最基本的變形來說明。

　　(1)預付年金轉化為普通年金

　　預付年金是指在一定時期內，各期期初等額的系列收付款項。它與後付年金的主要區別在於每期收付款項發生的時點不同，前者在期初，後者在期末。因為後付年會在現實生活中更常見，所以通常又稱之為普通年金。財務管理教科書中一般均以普通年金作為教學的霞點，分別介紹其現值和終值的計算，並且在教科書中附普通年金終值繫數表和普通年金現值繫數表，以方便相應的終值和現值的計算。而對於預付年會終值或現值的計算，一般是通過分析預付年金與普通年金之間的關係，利用普通年金終值繫數或現值繫數進行求解。但是現有的教科書中對於預付年金與普通年金之問的關係的分析都比較晦澀，學生理解較困難。

　　而利用現金流量圖可以使這種分析變得更直觀，從而方便學生理解和記憶。

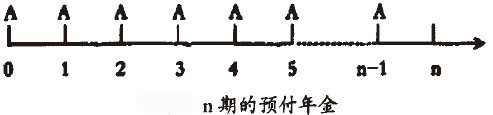
　　依據預付年金的定義，預付年金可以用下圖表示：

　　為了將預付年金轉換為普通年金，可以將預付年金中每期發生的款項向後“平移“一期，根據複利終值的計算公式，平移後每期發生額均為原發生額乘以一年期終值繫數，圖示如下：

　　很顯然，上圖正是一個標準的每期發生額為A(1+i)的n年期普通年金。據此，預付年金的現值和終值計算公式可以表示為：預付年金現值PVAin=A x(1+i)×PVIFAin；預付年金終值FVAin=A×(1+i)×FVIFAin。這樣預付年金終值或現值的計算可以根據普通年金終值繫數或普通年金現值繫數計算出來，即只要給定貼現率和期數，利用普通年金終(現)值繫數表就可以求出預付年金的終值或現值。

　　(2)遞延年金轉化為普通年金

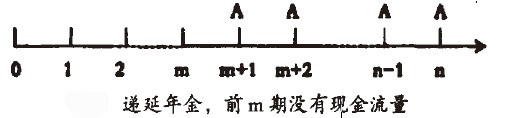
　　遞延年金是指在最初若幹期沒有收付款項的情況下，隨後若幹期有等額的系列收付款項。可以用下圖表示：

　　前m期沒有收付款項，從m+l期期末開始收付款項，共發生n-m期。遞延年金也可以根據定義式進行計算，只是計算量大、非常複雜，但利用現金流量圖將其轉化為普通年金問題進行計算則較為簡便。

　　比較遞延年金與普通年金容易發現，在整個n期內，僅在前m期內未發生等額收付款項，在之後的n-m期內，是典刑的等額系列收付款項。如果假設前rtl期也存在等額收付款項，則是一個n期的普通年金。在計算現值的時候，可以先計算n期普通年金的現值，然後把不存在的前m期的普通年金現值減去，就得到了結果，計算量大大減少。根據年金現值計算公式遞延年金現值為：PVA in=A×(PVIFA-PVIFAim),直接可以通過查表得出結果。

　　同樣可以推算遞延年金的終值計算公式，從而使遞延年金的終值計算轉換成普通年金終值計算。學生分析的過程大大簡化，提高了計算速度和準確性。