遞延年金現值

出自 MBA智库百科(https://wiki.mbalib.com/)

遞延年金現值是指間隔一定時期後每期期末或期初收入或付出的系列等額款項，按照複利計息方式折算的現時價值，即間隔一定時期後每期期末或期初等額收付資金的複利現值之和。

　　遞延年金現值是指若幹時期後開始每期款項的現值之和、其現值計算方法有三種。

　　第一種方法：把遞延年金視為“2”期普通年金，求出遞延期末(圖中“2”，所對應的位置)的現值，然後再將此現值調整到第一期的期初(圖中“0”對應的位置)。

　　其計算的基本步驟如下。

• 第一步，求出遞延期末的現值。

　　P_m=A·(P/A,i,n)

• 第二步，將遞延期末的現值調整到第一期期初。

　　P=P_m·(P/S,i,m)

• 綜合以上兩個計算步驟，則可得到遞延年金現值的計算公式之一。

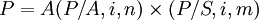
　　(例1)如上圖所示，假設銀行利率為6％，其遞延年金現值為多少?

　　解 P=A(P/A,i,n)(P/S,i,m)

　　=100×(P/A,6％,4)×(P/S,6％,2)

　　=(100×3．465×0．890)元

　　=308．4元

　　第二種方法：假設遞延期也發生款項的等額收付，則先求出包含遞延期在內，即(m+n)期的普通年金現值，然後扣除實際並未收付的遞延期(m)的普通年金現值，即可得出最終結果。

• 按此方法可得遞延年金現值計算公式之二。

　　P = P_{m + n} − P_m

　　依例1資料，計算其遞延年金現值。

　　解 P=A[(P/A,i,m+n)-(P/S,i,m)]

　　=100×[(P/A,6％,2+4)一(P/A,6％,2)]

　　=[100×(4．917-1．833)]元

　　=308．4元

　　第三種方法：先求出遞延年金的終值，再將其折算為現值。

　　其計算的基本步驟如下。

• 第一步，求出遞延年金的終值。

　　S=A(S/A,i,n)

• 第二步，將遞延年金的終值折算為現值。

　　P=S(P/S,i,m+n)

• 綜合以上兩個計算步驟，則可得到遞延年金現值的計算公式之三。

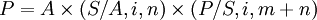
　　依例1資料，計算其遞延年金現值。

　　解 P=A(S/A,i,n)(P/S,i,m+n)

　　=100(S/A,6％,4)(P/S,6%,2+4)

　　=(100×4．375×0．705)元

　　=308．4元

　　(例2)小王是一個自由職業者，他從2004年1月起每月月末交納養老保險金120元，以便在30年以後的退休期間每月月未能領取一筆固定的養老金。假設養老金的月利率為o．36％，那麼，他在退休後的20年中每月能夠領取多少養老金?

　　分析：該問題中有兩個年金，一是從2004年1月起的360個月(至2033年12月)中每月月末發生120元的年金，這是普通年金；二是從2034年1月起的240個月(至2053年12月)每月月末發生的年金，這是遞延年金。可以以不同的時點為基準，建立交納養老金和領取養老金的現值相等關係。

　　解 假設小王退休後每月能領取的養老金為A元，下麵分別按照三個不同的時點來求A。

　　(1)以2004年1月初為基準日。

• 交納養老金的年金現值為

　　120×(P/A,0．36%,360)

• 領取養老金的年金現值為

　　A(P/A,0．36％,240)(P/S,0．36％,360)

• 這兩個現值應當相等，故得到下列方程。

　　120×(P/A,0．36％,360)＝A(P/A,0．36％,240)(P/S,0．36％,360)

• 計算上述方程中的繫數，代入上式，得

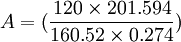　　元＝550．02元

　　(2)以2033年12月末(即2034年1月初)為基準日。

• 交納養老金的年金終值為

　　120×(S/A,0．36%,360)

• 領取養老金的年金現值為

　　A(P/A,0．36%,240)

• 這兩個值應當相等，故得到下列方程。

　　120×(S/A,0．36%,360)＝A(P/A,0．36%,240)

• 計算上述方程中的繫數，代入上式，得A＝(120×735．043)元＝549．50元

　　(3)以2053年12月末(即2054年1月初)為基準日。

• 交納養老金的年金終值為

　　120×(S/A,0．36%,360)×(S/P,0．36%,240)

• 領取養老金的年金終值為

　　A(S/A,0．36%,240)

• 這兩個終值應當相等，故得到下列方程。

　　120×(S/A,0．36%,360)×(S/P,0．36%,240)=A(S/A,0．36%,240)

• 計算上述方程中的繫數，代人上式，得

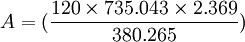　　元

　　以三個不同的時點為基準日，建立交納養老金和領取養老金的價值平衡關係，計算得到的結果是相同的(略有誤差是近似計算所致)。

• 遞延年金