套期保值比率
出自 MBA智库百科(https://wiki.mbalib.com/)
套期保值比率(Hedge Ratio)
目錄 |
套期保值比率的概念[1]
套期保值比率是指為規避固定收益債券現貨市場風險,套期保值者在建立交易頭寸時所確定的期貨合約的總價值與所保值的現貨合同總價值之間的比率。確定合適的套期保值比率是減少交叉套期保值風險,達到最佳套期保值效果的關鍵。
套期保值比率計算公式[1]
由於固定收益債券的票面利率有許多種,且大都不等於利率期貨合約的標的資產(一般都是虛擬券)規定的利率。因此,在運用利率期貨對固定收益債券進行套期保值時,固定收益債券現貨的價值與所需利率期貨合約的價值之間並不是1:1的關係,規避等量不同品種債券的利率風險時,在利率期貨市場上需要不同面值的期貨頭寸。而且基差風險的存在,會使套朗保值的效果受到很大影響,運用套期比率的概念,套期保值者能夠儘可能地降低基差風險的影響。
用利率期貨進行套期保值的目的是降低利率變動對固定收益債券資產價格的影響,降低利率風險。因此在完美套期保值下,現貨頭寸價格波動的損失應正好為期貨頭寸的盈利沖抵,即:
套期保值債券價格波動=期貨合約價格波動×套期保值比率
由此可得套期保值比率的計算公式:
|
套期保值比率= | 套期保值債券價格波動 | |
| 期貨合約價格波動 |
因此,套期保值比率應該等於現貨價格變動程度與期貨標的價格變動程度的比。如果套期保值債券的波動大於所用來進行套期保值期貨合約的波動,那麼套期保值比率應大於1。
譬如,假定長期國債期貨合約的標的債券是票面利率為3%的7年期虛擬國債,如果我們持有的債券票面利率為2.5%,期限是10年,那麼同國債期貨標的相比,該債券票面利率更高,期限更長,因此該債券價格受利率變化影響的程度更大,套期保值比率應大於1,即能夠用較少數量的國債期貨合約進行套期保值。如果債券價格波動性是期貨標的波動性的兩倍,那麼每一單位的現貨債券需要兩倍金額的國債期貨合約來為其保值。
套期保值比率的計算[1]
確定利率期貨套期保值比率最重要的因素是套期保值債券與利率期貨合約波動的計算。在債券分析中,衡量債券波動性的指標主要有久期和基點價值,相應地,利率期貨套期保值比率的計算方法有修正久期(duration)法、基點價值法
(一)修正久期法
1.久期
久期是衡量債券持有者收到全部現金付款的平均等待時間,反映了債券價格與市場利率變動的關係,是衡量債券對利率敏感性的重要指標。當市場利率發生波動時,債券價格絕對波動幅度與久期成正比,久期越大,價格波動就越大。在其他條件不變的情況下,債券期限越長,票面利率越低,久期越大。
久期的概念最初是由Macaulay提出的,隨後發展出多種不同的形式的久期,其中有麥考利久期(Macaulay duration)、修正久期、有效久期和關鍵年久期等。在假定收益率曲線平坦,並且用於所有未來現金流的貼現率固定不變的情況,麥考利久期的計算公式為:
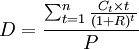
其中,D代表麥考利久期,t代表距償還利息和(或)本金的時間長度,Ct代表在時間t償還的利息和(或)本金,n代表債券到期日的時間長度,R代表利率,P代表債券貼現價格。其計算公式為:

債券的現值是將來所有本息的現值,因此,久期是債券本息償還時間的加權值,對應於t時的權重等於c時刻所有償還的本息現值占債券總現值的比率。在對現貨頭寸進行套期保值時,投資者關心的是利率變動對債券價格變動的影響。將上面債券價格公式關於利率及求導數:
![\frac{dP}{dR}=-\frac{1}{1+R}[\frac{C_1}{1+R}+\frac{2C_2}{(1+R)^2}+L+\frac{nC_n}{(1+R)^n}]](/w/images/math/c/8/8/c88a85a6dd4929a5ad3bf12cd236f8c3.png)
上式反映了利率發生微小變動時,債券價格的變動值。公式右邊括弧中正好是債券的麥考利久期。將公式兩邊同除以債券價格P,就可得到利率發生微小變動時,債券價格變動的百分比,即:
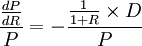
麥考利久期與(1+R)的比值通常稱為修正久期(modified duration,Dm):
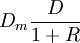
這表明,修正久期可以看做利率發生微小變動時所引起的債券價格的變動水平。
對於債券組合而言,其久期可以表示為組合中每隻債券久期的加權平均,權重等於各債券在組合中所占的比重,這可以用久期的計算公式推導得到。
2.利用久期計算套期保值比率
久期度量了債券價格隨利率變動時的波動特征,因此可以用來計算利率期貨套期保值比率。由於利率期貨合約價格近似等於最便宜可交割債券價格除以轉換因數,因此利率期貨合約的修正久期可以用最便宜可交割債券的修正久期除以轉換因數得到。從而我們可以計算出最優的套期保值比率:
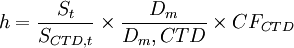
其中,St代表套期保值債券價值,SCTD,t代表最便宜可交割債券價值,Dm代表套期保值債券修正久期,Dm,CTD代表最便宜可交割債券修正久期,CFCTD代表最便宜可交割債券轉換因數。
由於久期概念存在一定的局限性,這使得久期法計算的最優套期接保值比率也存在一些缺點,但這些缺點並不會很嚴重,因為公式中力子和分母中都有久期,可以將其缺點部分抵消。
例如,2002年3月,某養老基金經理決定在5月中旬用價值100頂瑞士法郎(CHF)的短期存款購買債券組合,該基金經理預計利率將會下降,從而造成債券價格上漲,因此決定用CONF期貨(瑞士聯邦長期政府債券期貨,每張合約包含1咖張面值CHN0(的瑞士聯邦長期政府債券)進行套期保值,將債券價格鎖定在目前6t價格水平上。2002年3月份的市場情況見下表。
2002年3月份市場情況
| 債券組合市場價值 | CHF10000000 |
| CTD債券價格 | CHF98.74 |
| CONF期貨2002年6月合約價格 | CHF120.50 |
| 債券組合修正久期 | 7.00 |
| CTD債券修正久期 | 7.56 |
| CTD債券轉換因數 | 0.819391 |
利用修正久期法計算的套期保值比率為:

2002年3月份市場情況
| 債券組合市場價值 | CHF10210000 |
| CTD債券價格 | CHF101.01 |
| CONF期貨2002年6月合約價格 | CHF123.27 |
因此,該基金經理在3月中旬以CHFl20.50的價格買進77張2002年6月到期的CONF期貨合約。到5月中旬,市場利率果然下降,債券價格上揚(見上表)。於是該基金經理以每張合約CHN23.27的價格將持有的CONF期貨合約平倉,併在債券市場上買回價值CHFl0210 000的債券組合。結果該基金經理在期貨市場上所獲利潤不僅彌補了在債券上的虧損,而且還有盈餘CHF3290,套期保值是成功的(見下表)。
交易策略與結果
| 日期 | 債券組合現貨 | 期貨 |
| 3月15日 | 市場價值 CHF10000000 | 以CHF120.50的價格買進77張CONF期貨合約 |
| 5月15日 | 市場價值 CHF10210000 | 以CHF123.27的價格賣出77張CONF期貨合約 |
| 交易結果 | 虧損CHF210000 | 盈利CHF213290 |
(二)基點價值法
除了久期外,另一種衡量債券價格波動性的指標就是基點價值(basi。pointvalue,BPV),即債券收益率變化一個基點(0.01個百分點)時,債券價格的變化幅度(這裡的變化幅度指的是價格的變動額,而不是百分比)。即:
|
債券基點價值= | 債券價格變化幅度 | |
| 收益率變換幅度 |
利用債券的基點價值,可以計算出對債券進行套期保值的套期保值比率:
|
套期保值比率= | 套期保值債券價格波動 | |
| 期貨合約價格波動 |
=
| 套期保值債券價格波動 | ||
| 收益率波動 |
/
| 期貨合約價格波動 | ||
| 收益率波動 |
=
| 套期保值債券BPV | ||
| 期貨合約BPV |
由於利率期貨合約價格近似等於最便宜可交割債券除以轉換因數,因此利率期貨合約的基點價值近似等於最便宜可交割債券的基點價值除以其轉換因數,即:
|
期貨合約BPV= | CTD債券BPV | |
| CTD債券轉換因數 |
因此,
|
套期保值比率= | 套期保值債券BPV | |
| CTD債券BPV×CTD債券轉換因數 |
例如,在2002年3月份,某機構投資者持有價值EUR4咖萬的債券組合,並決定在2個月後進行減持。如果市場利率上揚,那麼該投資者將會有債券價格下跌的風險,為消除這一擔心,該投資者決定用歐洲債券期貨(每張合約包含100舊張面值EURl00的德國聯邦政府債券)進行套期保值,以鎖定價格,規避利率風險。2002年3月份的市場情況見下表。
2002年3月份市場情況
| 債券組合市場價值 | EUR40000000 |
| CTD債券價格 | EUR95.12 |
| 歐洲債券期貨2002年6月合約價格 | EUR106.00 |
| 債券組合基點價值 | EUR32800.00 |
| CTD債券基點價值 | EUR0.06763 |
| CTD債券轉換因數 | 0.897383 |
利用基點價值法計算的套期保值比率為:
h=\frac{32800.00}{0.06763\times1000}\times0.897383=435.22
2002年5月份市場情況
| 債券組合市場價值 | EUR39016000 |
| CTD債券價格 | EUR930391.10 |
| 歐洲債券期貨2002年6月合約價格 | EUR103.73 |
因此,該機構投資者持有債券組合可以通過在3月份以EUR106.00的價格賣出435張6日到期的歐洲債券組合期貨合約即可達到保值的目的。到5月份,利率果然上漲,債券組合價格下跌(5月的市場情況見上表)。於是改投資者賣出所有的債券組合,同時以EUR103.73買進435張歐洲債券期貨合約,將持有的期貨合約對沖。結果。該投資者在債券結果上的損失在期貨市場上得到了彌補(見下表)
交易策略與結果
| 日期 | 債券組合現貨 | 期貨 |
| 3月15日 | 市場價值 EUR40000000 | 以EUR106.00的價格賣出435張歐洲債券期貨合約 |
| 5月15日 | 市場價值 EUR39016000 | 以EUR103.73買進435張歐洲債券期貨合約 |
| 交易結果 | 虧損 EUR984000 | 盈利EUR987450 |
套期保值比率的調整[1]
分別用債券價格對利率變動的敏感性和對利率期貨合約價格的敏感性推導出了套期保值比率的計算公式。在這一過程中,隱含著這樣一個假定:最便宜可交割債券與被套期保值的債券之間的相對收益率差額是常數。我們並沒有考慮各種債券自身的其他特點,特別是在對不可交割債券進行套期保值時,被套期保值債券與最便宜可交割債券的一些不同特性如信用等級、利率水平、期限特征等,會使得二者收益率之間的差額處在不斷的變動之中,這會對套期保值的效果產生不利影響。因此,為保證套期保值的效果,在實際應用中,需要對前面計算得到的套期保值比率按照被套期保值債券的特征進行適當調整。
對利率期貨套期保值比率進行調整的常用方法是收益率;繫數法。具體做法是,用歷史數據建立被保值債券收益率與最便宜可交割債券收益之間的回歸方程:
rb = α + βrCTD + ε
其中,rb表示被套期保值債券的收益率,rCTD表示套期保值的CTD債券的收益率,ε是誤差項,α和β分別是截距和回歸繫數。
利用回歸分析可以得到繫數β的估計值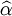 ,稱為收益率;(Yield beta),表示被套期保值債券與CTD債券收益率間的相對變動率,即被套期保值債券收益率受CTD債券收益率變動的影響程度。誤差項說明這兩種債券收益率之間的關係不是固定的,是有雜訊的。
,稱為收益率;(Yield beta),表示被套期保值債券與CTD債券收益率間的相對變動率,即被套期保值債券收益率受CTD債券收益率變動的影響程度。誤差項說明這兩種債券收益率之間的關係不是固定的,是有雜訊的。
利用收益率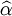 可以對套期保值比率進行調整,以消除被保值債券因信用風險等因素而造成的與CTD債券收益率之間的差異。
可以對套期保值比率進行調整,以消除被保值債券因信用風險等因素而造成的與CTD債券收益率之間的差異。
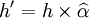 其中,
其中,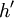 表示調整後的套期保值比率,h表示用修正久期法或基點價值法計算的套期保值比率。
表示調整後的套期保值比率,h表示用修正久期法或基點價值法計算的套期保值比率。
評論(共3條)
H=coefficient of the correlation of the two assets*sd. S\ sad. F
“假定長期國債期貨合約的標的債券是票面利率為3%的7年期虛擬國債,如果我們持有的債券票面利率為2.5%,期限是10年,那麼同國債期貨標的相比,該債券票面利率更高,期限更長,因此該債券價格受利率變化影響的程度更大,套期保值比率應大於1”此段中,國債期貨合約的標的債券票面利率:3%,債券票面利率為2.5%,為何說“債券票面利率更高,期限更長”?求解。








套期保值比率錯了,CTD債券轉換因數 應該在分子而不是分母