久期
出自 MBA智库百科(https://wiki.mbalib.com/)
久期(Duration)
目錄 |
什麼是久期(Duration) [1]
久期有許多不同的形式和解釋。幾種尤為重要的種類是麥考萊久期(Macaulay duration)、修正久期(Modified duration)、封閉式久期(Closed-form duration)和有效久期(Effective duration)。
麥考萊久期(Macaulay duration)
久期的概念最早是馬考勒(Macaulay)在1938年提出來的,所以又稱馬考勒久期(簡記為D)。馬考勒久期是使用加權平均數的形式計算債券的平均到期時間。它是債券在未來產生現金流的時間的加權平均,其權重是各期現金值在債券價格中所占的比重。
“久期”又叫“持續期”,要歸功於F.R•麥考萊,他在1938年提出要通過衡量債券的平均到期期限來研究債券的時間結構。當被運用於不可贖回債券時,麥考萊久期就是以年數表示的可用於彌補證券初始成本的貨幣加權平均時間價值。久期對於財務經理的主要價值在於它是衡量利率風險的直接方法,久期越長,利率風險越大。麥考萊久期有如下假設:收益率曲線是平坦的;用於所有未來現金流的貼現率是固定的。
保羅·薩繆爾森、約翰·斯克斯和瑞丁敦在隨後的若幹年獨立地發現了久期這一理論範疇,特別是保羅·薩繆爾森和瑞丁敦將久期用於衡量資產/負債的利率敏感性的研究,使得久期具有了第二種含義,即:資產針對利率變化的價格變化率。
久期--的第二個含義是債券投資管理中的一個極其重要的策略----“免疫策略”的理論基礎,根據該策略,當交易主體債券組合的久期與債權的持有期相等的時候,該交易主體短期內就實現了“免疫”的目標,即短期內的總財富不受利率波動的影響。
但是運用這一策略的前提則是,現有久期概念能否正確地衡量未來任何利率變動情景下債券價格的變動情況。
修正久期(Modified duration)
債券的修正久期幫助投資者理解,如果到期收益率(YTM)上升或下降1%,債券價格會上升或下降多少。
如果投資者擔心短期內利率會發生變化,這是一個重要的指標。具有半年付息的債券的修正久期可以用以下公式計算:
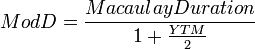
封閉式久期(Closed-form duration)
有效久期(Effective duration)
票面利率、到期時間、初始收益率是影響債券價格的利率敏感性的三個重要因素,它們與久期之間的關係也表現出一些規則。
- 1.保持其它因素不變,票面利率越低,息票債券的久期越長。
票面利率越高時,早期的現金流現值越大,占債券價格的權重越高,使時間的加權平均值越低,即久期越短。
- 2.保持其它因素不變,到期收益率越低,息票債券的久期越長。
到期收益率越低時,後期的現金流現值越大,在債券價格中所占的比重也越高,時間的加權平均值越高,久期越長。
- 3.一般來說,在其它因素不變的情況下,到期時間越長,久期越長。
債券的到期時間越長,價格的利率敏感性越強,這與債券的到期時間越長久期越長是一致的。但是,久期並不一定總隨著到期時間的增長而增長。
![MacD=\frac{\sum_{t=1}^T PV(c_t)\times t}{P}=\sum_{t=1}^T[\frac{PV(c_t)}{P}\times t]](/w/images/math/1/5/e/15e569d6a15bea19c72448931376c522.png) (公式1)
(公式1)
其中,
- MacD是馬考勒久期,
- P是債券當前的市場價格,
- PV(Ct)是債券未來第t期可現金流(利息或資本)的現值,
- T是債券的到期時間。
- t為從當前到t時刻現金流發生的持續時間。
- y為債券的風險程度相適應的收益率。假設未來所有現金流的貼現率都固定為y。
需要指出的是在債券發行時以及發行後,都可以計算馬考勒久期。計算發行時的馬考勒久期,T(到期時間)等於債券的期限;計算發行後的馬考勒久期,T(到期時間)小於債券的期限。
![MacD=\frac{1+r}{r}-\frac{1+r+N\times (c-r)}{c\times [(1+r)^N-1]+r}](/w/images/math/d/2/0/d2015efbad53a4e5e8cedbb2dab489e0.png)
- D為久期;
- c為票息率
- r為市場利率
- N為到期期限;
任一金融工具的久期公式一般可以表示為[2]:
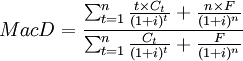 (公式2)
(公式2)
其中:
實際上,公式(公式3)的分母正是該金融工具的市場價值,因此,久期公式又可表示為:
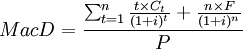 (公式3)
(公式3)
其中:P表示該金融工具的市場價值或價格。
久期的計算過程舉例[2]
下麵試舉一例來說明久期的計算過程。假設面額為1000元的3年期變通債券,每年支付一次息票,年息票率為10%,此時市場利率為12%,則該種債券的久期為:
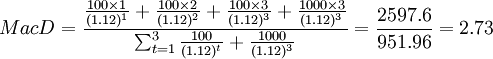 (年)
(年)
如果其他條件不變,市場利率下跌至5%,此時該種債券的久期為:
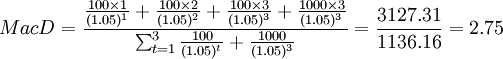 (年)
(年)
同理,如果其他條件不變,市場利率上升至20%,此時久期為:
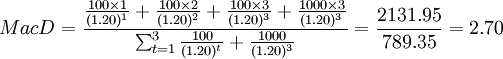 (年)
(年)
再者,如果其他條件不變,債券息票率為0,那麼:
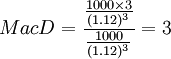 (年)
(年)
- 從上面的計算結果可以發現,久期隨著市場利率的下降而上升,隨著市場利率的升而下降,這說明兩者存在反比關係。此外,在持有期間不支付利息的金融工具,其久期等於到期期限或償還期限。那些分期付息的金融工具,其久期總是短於償還期限,是由於同等數量的現金流量,早兌付的比晚兌付的現值要高。金融工具到期期限越長其久期也越長;金融工具產生的現金流量越高,其久期越短。
- 1.只有貼現債券的馬考勒久期等於它們的到期時間
- 2.直接債券的馬考勒久期小於或等於它們的到期時間
馬考勒久期與債券價格的關係
對於給定的收益率變動幅度,馬考勒久期越大,債券價格的波動幅度越大:
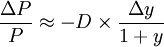
到期時間、息票率、到期收益率是決定債券價格的關鍵因素,與久期存在以下的關係:
- 1.零息票債券的久期等於到它的到期時間。
- 2.到期日不變,債券的久期隨息票據利率的降低而延長。
- 3.息票據利率不變,債券的久期隨到期時間的增加而增加。
- 4.其他因素不變,債券的到期收益率較低時,息票債券的久期較長。
債券的凸性準確地描述了債券價格與收益率之間非線性的反向關係;而久期將債券價格與收益率之間的反向關係視為線性的(一階導數關係),只是一個近似公式。
凸性(C),實際上描述了債券價格和收益率的二階導數關係。定義如下:
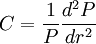
凸性(C)和馬考勒久期(D)一起,可以更加準確地反映利率變動對債券價格的影響:
(泰勒級數二級展開)
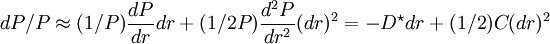
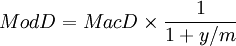
通常,久期值還得再除以1+y/m加以修正,y即債務工具的收益率,m為每年發生現金流的次數,這個修正久期用ModD表示,即ModD =MacD/(1+y/m)。
在債券分析中,久期已經超越了時間的概念,投資者更多地把它用來衡量債券價格變動對利率變化的敏感度,並且經過一定的修正,以使其能精確地量化利率變動給債券價格造成的影響。修正久期越大,債券價格對收益率的變動就越敏感,收益率上升所引起的債券價格下降幅度就越大,而收益率下降所引起的債券價格上升幅度也越大。可見,同等要素條件下,修正久期小的債券比修正久期大的債券抗利率上升風險能力強,但抗利率下降風險能力較弱。
正是久期的上述特征給我們的債券投資提供了參照。當我們判斷當前的利率水平存在上升可能,就可以集中投資於短期品種、縮短債券久期;而當我們判斷當前的利率水平有可能下降,則拉長債券久期、加大長期債券的投資,這就可以幫助我們在債市的上漲中獲得更高的溢價。
需要說明的是,久期的概念不僅廣泛應用在個券上,而且廣泛應用在債券的投資組合中。一個長久期的債券和一個短久期的債券可以組合一個中等久期的債券投資組合,而增加某一類債券的投資比例又可以使該組合的久期向該類債券的久期傾斜。所以,當投資者在進行大資金運作時,準確判斷好未來的利率走勢後,然後就是確定債券投資組合的久期,在該久期確定的情況下,靈活調整各類債券的權重,基本上就能達到預期的效果。
久期是一種測度債券發生現金流的加權平均期限的方法。由於債券價格敏感性會隨著到期時間的增長而增加,久期也可用來測度債券對利率變化的敏感性,根據債券的每次息票利息或本金的支付時間的加權平均來計算久期。
久期的計算就當是在算加權平均數。其中變數是時間,權數是每一期的現金流量,價格就相當於是權數的總和(因為價格是用現金流貼現算出來的)。這樣一來,久期的計算公式就是一個加權平均數的公式了,因此,它可以被看成是收回成本的平均時間。
決定久期即影響債券價格對市場利率變化的敏感性包括三要素:到期時間、息票利率和到期收益率。
不同債券價格對市場利率變動的敏感性不一樣。債券久期是衡量這種敏感性最重要和最主要的標準。久期等於利率變動一個單位所引起的價格變動。如市場利率變動1%,債券的價格變動3,則久期是3。
實際上,久期在數值上和債券的剩餘期限近似,但又有別於債券的剩餘期限。在債券投資里,久期被用來衡量債券或者債券組合的利率風險,它對投資者有效把握投資節奏有很大的幫助。
一般來說,久期和債券的到期收益率成反比,和債券的剩餘年限及票面利率成正比。但對於一個普通的附息債券,如果債券的票面利率和其當前的收益率相當的話,該債券的久期就等於其剩餘年限。還有一個特殊的情況是,當一個債券是貼現發行的無票面利率債券,那麼該債券的剩餘年限就是其久期。這也是為什麼人們常常把久期和債券的剩餘年限相提並論的原因。
另一種說法:久期是債券平均有效期的一個測度,它被定義為到每一債券距離到期的時間的加權平均值,其權重與支付的現值成比例 。
久期是考慮了債券現金流現值的因素後測算的債券實際到期日。價格與收益率之間是一個非線性關係。但是在價格變動不大時,這個非線性關係可以近似地看成一個線性關係。也就是說,價格與收益率的變化幅度是成反比的。值得註意的是,對於不同的債券,在不同的日期,這個反比的比率是不相同的。
久期的案例分析[3]
某附息債券的面值為1000元,剩餘期限為3年,票面年利率為8%,每年付息一次。該債券市場價格為950.25元,因此該債券的到期收益率為10.00%。請計算該債券的久期是多少?
解:該附息債券剩餘期限內會收回3筆現金流,分別是第一年的利息80元,第二年的利息80元,第三年的本金和利息之和1080元。現金流收回時間和現金流金額分別是表1中的第一列和第二列。三筆現金流發生的時間不一樣,因此對應的現值(貼現)因數也不一樣。按照三個貼現因數,三筆現金流貼現到現在的現值分別是72.73元、66.12元和811.40元。貼現計算如下:
第一筆現金流貼現值=第一筆現金流金額×第一筆現金流貼現因數
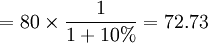 (元)
(元)第二筆現金流貼現值=第二筆現金流金額×第二筆現金流貼現因數
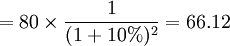 (元)
(元)第三筆現金流貼現值=第三筆現金流金額×第三筆現金流貼現因數
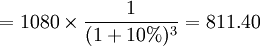 (元)
(元) 其中,第一筆現金流貼現因數為 ,第二筆現金流貼現因數為
,第二筆現金流貼現因數為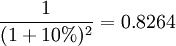 ,第三筆現金流貼現因數為
,第三筆現金流貼現因數為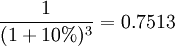 。貼現因數和現金流現值分別是表5.2中的第三列和第四列。
。貼現因數和現金流現值分別是表5.2中的第三列和第四列。
現金流之和950.25即為債券價格P0,表1的第五列是各期現金流現值PV(Ct)和現金流收回時間t的乘積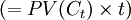 ,以及乘積之和2639.17元
,以及乘積之和2639.17元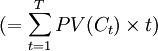 。用乘積之和除以P0就得到債券的久期為2.78年。
。用乘積之和除以P0就得到債券的久期為2.78年。
久期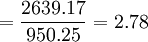 (年)
(年)
表1 久期計算細表
| 現金流收回時間 | 現金流金額 | 現值(貼現)因數 | 現金流現值 | 現金流現值×現金流收回時間 |
| 1 | 80 | 0.9091 | 72.73 | 72.73 |
| 2 | 80 | 0.8264 | 66.12 | 132.23 |
| 3 | 1080 | 0.7513 | 811.40 | 2434.21 |
| 950.25 | 2639.17 |
- ↑ Bond duration-Wikipedia
- ↑ 2.0 2.1 鄭鳴.商業銀行管理學[M].清華大學出版社, 2005.ISBN:7302101256, 9787302101253
- ↑ 岑仲迪 顧鋒娟編著.證券投資學.清華大學出版社,2011.02.
本条目由以下用户参与贡献
Lolo,Zfj3000,Angle Roh,Dan,Ania,Dionwang,Vulture,Dawinetion,Franklee0415,Guyu1016,风行水使,Scuibk,Cqzxmw,Yixi,连晓雾,林巧玲,可恨密码记不住,方小莉,李文诚,苏青荇,〢.蔠嚸,LuyinT,M id 731f627d96217404746689a7b388d1a5,AleAle.評論(共33條)
有點簡單了,不知是否可以補充得更詳細一些?
已對內容進行了補充,期待網友參與完善
謝謝您的貢獻,MBA智庫百科的發展離不開大家的參與及完善
“需要說明的是,久期的概念不僅廣泛應用在個券上,而且廣泛應用在債券的投資組合中。一個長久期的債券和一個短久期的債券可以組合一個中等久期的債券投資組合,而增加某一類債券的投資比例又可以使該組合的久期向該類債券的久期傾斜。所以,當投資者在進行大資金運作時,準確判斷好未來的利率走勢後,然後就是確定債券投資組合的久期,在該久期確定的情況下,靈活調整各類債券的權重,基本上就能達到預期的效果。”
這裡可以再具體說明下麽?
公式要這麼複雜麽?
還好啦 只用到求和、一階導數,沒有用更複雜的高等數學~
久期這一概念已經被廣泛用來檢測交易組合對於利率曲線的風險暴露。顧名思義,金融產品的久期是指投資人收到一比投資的所有現金流支付平均需要等待的時間。一個N年期零利息國債的久期為N年,而一個N年帶息(coupon-bearing)國債的久期小於N年,這是因為國債持有人在N年之前就已經收到某些現金流支付。---詳細見《風險管理與金融機構》(《risk management and financial institutions》)作者:約翰。赫爾(John C.Hull)多倫多大學
到期日不變,債券的久期隨息票據利率的降低而延長。 一般來說,久期和債券的到期收益率成反比,和債券的剩餘年限及票面利率成正比。這篇文章自相矛盾啊,久期和票面利率成反比!!!請改正。
到期日不變,債券的久期隨息票據利率的降低而延長。 一般來說,久期和債券的到期收益率成反比,和債券的剩餘年限及票面利率成正比。這篇文章自相矛盾啊,久期和票面利率成反比!!!請改正。
也有相同疑問。 請學習精湛者賜教。
可否對“免疫策略”加以分析?
可參考條目免疫策略,希望對您有幫助!~
智庫真是太牛啦,我英語教科書上面難以理解的知識點這裡都有解釋,我一本教科書1000人民幣這裡的知識全部不用收費哈哈,光憑這點還是我們中國好啊~~
是很專業啊,大學數學以前太荒廢了。
"一般來說,久期和債券的到期收益率成反比,和債券的剩餘年限及票面利率成正比。但對於一個普通的附息債券,如果債券的票面利率和其當前的收益率相當的話,該債券的久期就等於其剩餘年限。 " 這一段有問題有問題。票面利率等於當前收益率久期也小於剩餘年限;票面利率與久期的關係也不對。
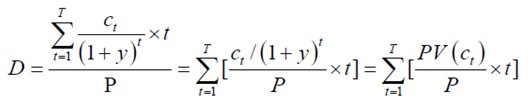








有點簡單了,不知是否可以補充得更詳細一些?