有效久期

出自 MBA智库百科(https://wiki.mbalib.com/)

有效久期(Effective Duration)

　　有效久期是指在利率水平發生特定變化的情況下債券價格變動的百分比。它直接運用不同收益率變動為基礎的債券價格進行計算，這些價格反映了隱含期權價值的變動。

　　弗蘭克•法波齊(Frank Fabozzi)描述了另一種衡量久期的方法，它是從修正久期的含義發展而來的。有效久期是衡量不同利率水平下債券價格敏感性的方法。在收益率發生很小變動時它是修正久期的近似值。有效久期對可贖回債券或其他期限和現金流不確定的證券尤為有用。

　　在Macaulay久期模型研究中存在一個重要假設，即隨著利率的波動，債券的現金流不會發生變化。然而這一假設對於具有隱含期權的金融工具，如按揭貸款、可贖回(或可賣出)債券等而言則很難成立。因此，Macaulay久期模型不應被用來衡量現金流易受到利率變動影響的金融工具的利率風險。針對Macaulay久期模型這一局限，FrankFabozzi提出了有效久期的思想。所謂有效久期是指在利率水平發生特定變化的情況下債券價格變動的百分比。它直接運用不同收益率變動為基礎的債券價格進行計算，這些價格反映了隱含期權價值的變動。

　　有效久期不需要考慮各期現金流的變化情況，不包含利率變化導致現金流發生變化的具體時間，而只考慮利率一定變化下的價格總體情況。因此，有效久期能夠較準確地衡量具有隱含期權性質的金融工具的利率風險。對於沒有隱含期權的金融工具，有效久期與修正久期是相等的。

　　隨著對久期模型研究的不斷深入，相繼有人提出了方向久期、偏久期、關鍵利率久期、近似久期以及風險調整久期等新的久期模型，把利率的期限結構、票息率的改變以及信用風險、贖回條款等加入到模型裡面，使久期模型得到了進一步的發展。

　　用下列公式可以計算有效久期：

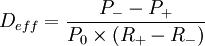
　　其中：

• P_——利率下降x個基本點時的債券價格；
• P+——利率上升x個基本點時的債券價格；
• R_——初始收益率減去x個基本點；
• R+——初始收益率加上x個基本點；
• P0——債券的初始價格。

　　例：考慮8年期利率為9.5％的債券，半年支付1次利息，按面值90％出售，其到期收益率為11.44％。我們現在用收益率中5個基本點的變化來計算其有效持續期。收益率為11.49％時，相關債券價格為89.77％元，收益率11.39％時，價格為90.25％。

• 修正持久期
• 麥考利久期