加權算術平均數
出自 MBA智库百科(https://wiki.mbalib.com/)
加權算術平均數(Weighted Arithmetic Mean)
目錄 |
加權算術平均數是具有不同比重的數據(或平均數)的算術平均數。
比重也稱為權重,數據的權重反映了該變數在總體中的相對重要性,每種變數的權重的確定與一定的理論經驗或變數在總體中的比重有關。依據各個數據的重要性繫數(即權重)進行相乘後再相加求和,就是加權和。加權和與所有權重之和的比等於加權算術平均數。加權算術平均數主要用於原始資料已經分組,並得出次數分佈的條件。
根據分組整理的數據計算的算術平均數。其計算公式為:
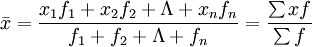
式中:f代表各組變數值出現的頻數。
例:以下表為例,計算人均日產量。
某企業50名工人加工零件均值計算表
| 按零件數分組 | 組中值x | 頻數f | xf |
|---|---|---|---|
| 105~110 110~115 115~120 120~125 125~130 130~135 135~140 | 107.5 112.5 117.5 122.5 127.5 132.5 137.5 | 3 5 8 14 10 6 4 | 322.5 562.5 940.0 1715.0 1275.0 795.0 550.0 |
| 合計 | – | 50 | 6160.0 |
解:平均日產量=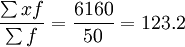 (件)
(件)
這種根據已分組整理的數據計算的算術平均數就稱為加權算術平均數。這時,算術平均數的大小,不僅取決於研究對象的變數值,而且受各變數值重覆出現的頻數(f)或頻率(f/∑f)大小的影響,如果某一組的頻數或頻率較大,說明該組的數據較多,那麼該組數據的大小對算術平均數的影響就大,反之則小。可見各組頻數的多少(或頻率的高低)對平均的結果起著一種權衡輕重的作用,因而這一衡量變數值相對重要性的數值稱為權數。這裡所謂權數的大小,並不是以權數本身值的大小而言的,而是指各組單位數占總體單位數的比重,即權數繫數(f/∑f)。權數繫數亦稱為頻率,是一種結構相對數。
當然,利用組中值作為本組平均值計算算術平均數,是在各組內的標誌值分佈均勻的假定下。計算結果與未分組數列的相應結果可能會有一些偏差,應用時應予以註意。在統計分析過程中,如果搜集到的是經過初步整理的次級數據,或數據要求不很精確的原始數據資料可用此法計算均值。如果要求結果十分精確,那麼需用原始數據的全部實際信息,如果計算量很大,可藉助電腦的統計功能。
如果是計算相對數的平均數,則應符合所求的相對數本身的公式,將分子視為總體標誌總量,分母視為總體單位總量。
例:某季度某工業公司18個工業企業產值計劃完成程式資料如下表,計算平均產值計劃完成程度。
某工業公司產值完成情況表
| 產值計劃完成程度(%) | 組中值(%) x | 企業數(個) | 計劃產值(萬元) f | 實際產值(萬元) xf |
|---|---|---|---|---|
| 80~90 90~100 100~110 110~120 | 85 95 105 115 | 2 3 10 3 | 800 2500 17200 4400 | 680 2375 18060 5060 |
| 合計 | - | 18 | 24900 | 26175 |
計劃完成相對數的計算公式是實際完成數與計劃任務數之比,因此,平均計劃完成程度的計算只能是所有企業的實際完成數與其計劃任務數之比,不能把各個企業的計劃完成百分數簡單平均。
評論(共6條)
什麼時候用普通演算法,什麼時候更適合用加權平均法?
頻數或所占比重不同的時候用加權~
在什麼條件下,加權算術平均數等於普通算術平均數?
加權各項的重要性一致的時候
在什麼條件下,加權算術平均數等於普通算術平均數?
在各數值權重相等時,加權平均=算術平均








在什麼條件下,加權算術平均數等於普通算術平均數?