麥卡勒姆規則
出自 MBA智库百科(https://wiki.mbalib.com/)
麥卡勒姆規則(McCallum Rule)
目錄 |
麥卡勒姆規則簡介[1]
麥克勒姆規則又被稱為基礎貨幣——名義GDP目標規則。與泰勒規則一樣,它也是一個適應性政策方程,但具有不同的政策工具及其背後的不同的貨幣政策傳導機制。麥克勒姆規則的政策工具是基礎貨幣而不是聯邦基金名義利率。根據這一規則,基礎貨幣增長率依名義GDP增長率(或水平值)與設定的目標之間的離差而變動。這一規則中也包含了基礎貨幣增長率的變化,在基礎貨幣增長率變化不是很大時,名義GDP目標和基礎貨幣目標可以說是等同的。
麥克勒姆規則包含三個主要部分:(1)名義GDP增長目標;(2)貨幣流通速度變化的移動平均值(即,相對於名義GDP的貨幣需求的變化);(3)名義與實際GDP之差。
- (一)麥卡勒姆一梅爾澤的基礎貨幣規則
在以貨幣供應量為主要中介目標的20世紀80年代,基礎貨幣是中央銀行的一個重要操作工具。在這樣的歷史背景下,麥卡勒姆(1988)提出了一個基礎貨幣規則,即中央銀行遵循這個規則,根據巨集觀經濟條件的變化對基礎貨幣做出相應調整。幾乎與此同時,梅爾澤(Meltzer)(1987)提出了相似的規則,因此也有人將此規則稱為麥卡勒姆一梅爾澤規則。其表達式為:
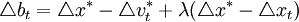
其中,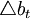 是基礎貨幣對數值的變化,即基礎貨幣在(t-1)到t期之間的增長率;
是基礎貨幣對數值的變化,即基礎貨幣在(t-1)到t期之間的增長率;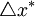 是名義GDP的目標增長率(麥卡勒姆賦值為4.5%),其目標值等於(
是名義GDP的目標增長率(麥卡勒姆賦值為4.5%),其目標值等於(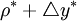 ),
),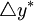 是實際GDP的長期平均增長率。該規則表達式右邊的第二項
是實際GDP的長期平均增長率。該規則表達式右邊的第二項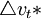 是前16個季度基礎貨幣流通速度的平均增長率,vt = xt − bt為基礎貨幣流通速度對數。這反映了由於技術進步或制度變化(假設為永久性變化)導致的對基礎貨幣需求的長期持續變化,而不是為了反映經濟景氣情況。最後一項是誤差校正項,該項表明當
是前16個季度基礎貨幣流通速度的平均增長率,vt = xt − bt為基礎貨幣流通速度對數。這反映了由於技術進步或制度變化(假設為永久性變化)導致的對基礎貨幣需求的長期持續變化,而不是為了反映經濟景氣情況。最後一項是誤差校正項,該項表明當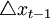 。低於
。低於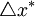 時,基礎貨幣的增長速度就要調高以彌補目標的誤差,麥卡勒姆選擇其繫數λ=0.5。
時,基礎貨幣的增長速度就要調高以彌補目標的誤差,麥卡勒姆選擇其繫數λ=0.5。
該規則的最終目標是穩定名義收入(名義GDP或名義GNP),因此,基礎貨幣必鬚根據名義收入的實際增長率與目標增長率之間的差距進行階段性調整。也有人將麥卡勒姆的這個規則稱為名義收入目標規則。
麥卡勒姆用這個規則對美國1954~1985年的季度數據進行驗證,他假設中央銀行的目標通貨膨脹率為0,根據美國曆史上真實產出的長期增長率大概為3%,因此可以假設名義GDP的年增長目標為3%。通過比較名義GDP偏離其目標路徑的均方差可以發現,使用麥卡勒姆規則可以使名義GDP非常緊密地靠近目標路徑。
不可否認,不管是麥卡勒姆規則還是泰勒規則,他們的初衷都是為了降低通貨膨脹率、減少經濟波動。但實際上,在對英國20世紀80年代的貨幣政策的檢驗中,這兩個規則卻給出了完全不同的結論:麥卡勒姆規則認為應該緊縮政策,而泰勒規則認為應該放鬆,實際上面對當時快速上升的高通貨膨脹,緊縮政策可能更合理。因此儘管泰勒規則更受青睞,而且目前大部分國家都採用利率作為貨幣政策工具,但在政策決策時也不能僅機械地遵循一種規則。
- (二)麥卡勒姆一納爾遜利率規則
儘管與泰勒規則相比,麥卡勒姆基礎貨幣規則中的所有變數都更容易測量,但基礎貨幣本身的測量卻有點麻煩,像在美國,由於很不穩定,這個變數只在很短時間的樣本中用過(1979~1982年)。因此,麥卡勒姆和納爾遜(1999)從基礎貨幣規則轉向了利率規則(聯邦基金利率),其表達形式就像上式中的誤差校正項:
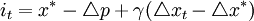
其中,it為名義利率,p是一般價格水平的對數,參數γ比λ大(麥卡勒姆取γ值為1.5)。之所以將貨幣政策工具由基礎貨幣轉向利率,除了數據的可得性原因之外,還因為他們相信基礎貨幣流通速度和聯邦基金利率之間具有穩定的關係,即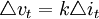 ,而
,而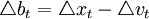 ,根據基礎貨幣規則,有:
,根據基礎貨幣規則,有:
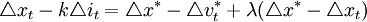
整理後得到:
![\triangle i_t=[\triangle v_t^*+(1+\lambda)(\triangle x_t-\triangle x^*)]/k](/w/images/math/0/4/8/048c6ffc5d01f561e7d988daa55d8ca9.png)
即得到聯邦基金利率變化的規則。
麥卡勒姆規則的產生背景[2]
從1970年代初開始,美國貨幣當局採用弗里德曼的政策主張,以保持穩定的貨幣增長率。從實際效果看,在此後近十年的時間內,貨幣增長率相對穩定,但產出和通貨膨脹卻出現了劇烈波動。於是,人們便懷疑貨幣供應量目標的有效性。面對這些問題,麥卡勒姆認為弗里德曼規則是在假定貨幣需求和貨幣流通速度不變的前提下保持貨幣供應量以固定的比例增長,顯然,這些前提並不能得到滿足。因此,基礎貨幣應根據貨幣流通速度和目標變數的變化進行階段性調整,才能使該規則具有更強的適應性。
麥卡勒姆規則是在弗里德曼規則(Friedman,1982)的基礎上發展起來的,它對後者作了三個重要修正。一是以基礎貨幣(而不是弗里德曼主張的貨幣供應量)為工具。因為貨幣供應量既不是貨幣政策的最終目標,也不是中央銀行可直接控制的政策工具,因此,在發生重大制度變遷時,中央銀行不能使其達到預定目標,而基礎貨幣則不然,在一定條件和相關的財政政策配合下,調控基礎貨幣可能達到預定目標。二是考慮了基礎貨幣流通速度的變化。
基礎貨幣應當根據流通速度的變化進行階段性調整,即兩者呈反方向變化。如果基礎貨幣以不變的比率增長,則不但達不到合意的目標,反而會加劇貨幣供應量和實際經濟的波動。三是把穩定名義收入作為貨幣政策的最終目標。因而,基礎貨幣必鬚根據名義收入的實際增長率與目標增長率之間的差距進行階段性調整。心。由於名義收入與價格水平和真實產出之間存在恆定的關係,所以,以名義收入為目標的優點之一便是可間接地控制通貨膨脹。
麥卡勒姆規則被提出後,一些經濟學家利用貨幣政策的實踐對其進行了實證檢驗,以考察使用麥卡勒姆規則(或它的擴展形式)在穩定通貨膨脹和實際產出方面的影響。麥卡勒姆本人(MeCallum,1987)利用美國1954—1985年的歷史數據,對麥卡勒姆規則的原式進行了回歸分析,結果顯示,使用該規則可使名義國民生產總值(GNP)非常緊密地靠近目標路徑。同時,模型還考察了名義收入缺口的反應繫數入取不同值時的情況,相比較而言,原式的效果更好。Croushore和Stark(1995)選擇了三種巨集觀經濟模型(凱恩斯主義模型、PSTAR+模型和理性預期模型)來模擬運用麥卡勒姆規則時經濟的運轉情況。從模擬的結果看,如果按麥卡勒姆規則進行操作,平均真實產出可接近其潛在水平,同時,模擬的價格大大低於歷史水平。然而,只有在PSTAR+模型中,實際GNP和價格水平兩者才都是穩定的。
Judd和Motley(1991)則考察了在凱恩斯模型、真實商業迴圈模型和向量自回歸模型三種模型下麥卡勒姆規則及其擴展形式(主要是修正後的名義GNP規則和價格水平規則)的表現。在大多數情況下,使用規則時通貨膨脹的波動要比沒有規則時小,唯一例外的是修正後的名義GNP規則在真實商業迴圈模型假設下通貨膨脹的波動比沒有規則時更寬。在三種規則的對比中,名義GNP規則在各種不同的模型中比其他規則具有更強的穩定性。為了檢驗麥卡勒姆規則是否會帶來更大的產出波動,他們還考察了名義GNP規則在1989年的兩季度中實際GNP增長率的表現。在實際商業迴圈模型中,所有規則對實際GNP的增長都沒有影響;而在其他模型中,使用規則的波動在多數時候要比不使用規則時更大一些。這說明,使用規則可能會增加實際GNP的短期波動性。此後,Judd和Motley(1993)又對以利率工具為變數的麥卡勒姆規則進行了檢驗。從結果來看,使用以基礎貨幣為工具、名義國內生產總值(GDP)為目標的規則所導致的平均通貨膨脹率最低,遠低於實際值5.4%,而且最為穩定。而以利率為工具的規則在大多數情況下可能有很高的置信度來保證使通貨膨脹率在接近於零的小範圍內波動,但是在僅有比例項的情況下可能導致發散性的情況。
如果從實證分析方面考慮,與其他規則相比,麥卡勒姆規則更加適合於中國的現實。這是因為:第一,麥卡勒姆規則以基礎貨幣為控制工具,這和中國中央銀行的政策工具是相同的。第二,麥卡勒姆規則無需分別估計通貨膨脹缺口和真實產出缺口,而只需估計名義GDP缺口。這與中國每年只公佈名義GDP目標(即產出目標)而沒有相應的通貨膨脹目標和實際產出目標的情況相吻合。正是從這種角度出發,選擇麥卡勒姆規則對中國的貨幣政策操作進行實際檢驗。但在實際運用過程中,需要根據中國的實際情況對一些變數和參數進行相應的調整。首先,對於麥卡勒姆規則反應函數的具體形式,包括工具和目標變數的選擇以及參數的取值,都沒有統一的看法。由於真實GDP的潛在增長率的可預測性較弱,在模型中剔除了這一變數,僅考慮名義GDP及其增長率。同時,根據已有數據估計反應函數的參數值,並計算出規則模擬的基礎貨幣及其增長率,以便於比較其與實際值的偏差。其次,麥卡勒姆規則原本是建立在浮動匯率制的基礎上,但中國實行的是盯住美元的匯率制度。為維持匯率穩定,中央銀行必須在市場進行外匯買賣操作,而這一過程又會導致基礎貨幣投放量的變化。因此,在建立反應函數時,需考慮固定匯率制度的影響。
麥卡勒姆規則的擴展[3]
麥卡勒姆規則產生以後。許多經濟學家從許多方面擴展了該規則(具體來說。主要包括以下兩個方面:
- 1.對規則目標的擴展
麥卡勒姆重新構造了以通貨膨脹為目標的基礎貨幣規則。規則的形式為,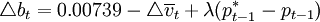 (1)
(1)
其中,pt − 1表示前一期的通貨膨脹,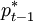 表示中央銀行的通貨膨脹目標。
表示中央銀行的通貨膨脹目標。
賈德和莫特利則將名義收入目標分解為真實收入目標(y)和通貨膨脹目標(p)。具體的規則形式如下:
![\triangle b_t=(\triangle y^f_t+\triangle p_t^*)-\triangle\overline{v}_{t-1}+\lambda[(y^f_{t-1}-y_{t-1})+(\triangle p_{t-1}^*-\triangle p_{t-1})]](/w/images/math/e/a/c/eac6ed60e56c5417dc386f95198a4056.png) (2)
(2)
為了考察上述規則和穩健性。他們使用了菲利浦斯曲線模型、真實經濟周期模型和向量自回歸模型等巨集觀經濟結構模型。比較這些規則在不同的模型假設之下的表現。結果發現。與沒有規則時相比。使用上述規則可以使平均通貨膨脹率為零。而且還可以使通貨膨脹的波動比沒有規則時小得多(但是總體來看。規則(1)和(2)的穩健性不如規則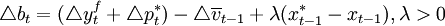 。因為當反應繫數;的取值超過一定的範圍。規則(1)和(2)在一些模型假設下可能會導致發散性的結果。
。因為當反應繫數;的取值超過一定的範圍。規則(1)和(2)在一些模型假設下可能會導致發散性的結果。
杜克爾和費希爾考察了貨幣當局具有多重目標時的情形(在他們的模型中。中央銀行以穩定價格和匯率為目標。並且允許參數隨時間的變化而變化。而霍爾等人在一篇文章中曾經使用預期的名義收入為目標。考察英國的貨幣政策(模型的形式為:

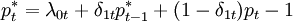
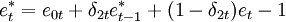 (3)
(3)
其中p、e為分別是以對數來衡量的價格水平和匯率;p * ,e * 是它們的目標值;λmt,m = 0,1,2是服從馬爾科夫轉換過程的參數;ε為隨機擾動。且ε-N(0,σε)。
不過根據麥卡勒姆的研究。這種前瞻性的名義收入規則有很強的模型依賴性。因此。在穩健性方面要大大低於簡單的麥卡勒姆規則。
- 2.對規則工具的擴展
麥卡勒姆考察了使用短期利率(90天的國庫券收益率)為工具的名義收入規則(不過。他認為名義利率與通貨膨脹之間的動態關係是使用該規則的一大難點。因為一般看來。高利率可以降低需求。從而減輕通貨膨脹壓力。但是。從較長時期來看。高利率又是加速通貨膨脹的結果。
因此。這就出現了一個相互矛盾的結論,為了實現低利率。中央銀行需要就必須提高利率以便降低通貨膨脹。儘管如此。麥卡勒姆還是考察瞭如下利率規則:
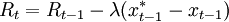 (3)
(3)
其中R表示短期利率,繫數λ為正。
但是。麥卡勒姆對上述利率規則的模擬結果卻不盡如人意λ的最優取值在0.03左右。而且會比麥卡勒姆的原式導致更大的均方根差。如果λ的取值充分低於0.03。則該利率規則無法提供足夠的反饋。因而不能保持名義收入接近其目標路徑;如果;的取值超過0.03(如;λ=0.05),就會出現發散性擺動(因此。麥卡勒姆將滯後兩期的名義收入引入利率規則。希望考察利率的穩定性。規則的形式為:。
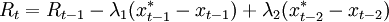 。
。
假設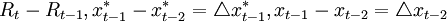 那麼上式可化為:
那麼上式可化為:
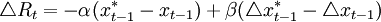 (4)
(4)
其中,α = λ1 − λ2,β = λ2其中右邊第一項表示名義收入缺口的比例項,第二項表示名義收入缺口的導數項。即名義收入增長率的變動;模擬的結果表明,當λ1 = 1.0,λ20.9時,上述規則明顯可以以極高的概率收斂到名義收入的目標值。不過這個結果具有欺騙性:雖然名義收入的總量達到了目標值,但檢查價格水平和產出的增長路徑可以發現,真實產出的增長率幾乎為零,而價格水平具有一個大於零的值,因此,上述規則並沒有達到穩定價格的目標。
McCaIlum規則在西方發達國家的應用比較[4]
McCallum認為,美國在20世紀的整個70年代,實際利率值低於按照其規則計算的理論利率值,說明這一時期美國的貨幣政策比較寬鬆。這與當時美國正面臨著嚴重的通貨膨脹,需要採取緊縮的貨幣政策是相吻合的,McCallum規則符合這一時期的實際情況。進入80年代之後,直到1987年,按照McCallum規則計算的結論,貨幣政策又過於緊縮。1987年~1996年,按照規則貨幣政策比較合適;但1996年之後貨幣政策又有些緊縮。
在英國,McCallum規則說明,整個20世紀70年代的貨幣政策太鬆了。因為按照規則,要求1973年的利率為38%,而實際的利率值僅為10.4%。1983年~1987年,貨幣政策又稍緊。自1987年之後,除1994年,貨幣政策都是比較適宜的。
日本的情況也一樣,McCallum規則說明,1973年~1978年應該稍緊一些,1982年~1987年間的大部分時間,貨幣政策卻又過於緊縮。而1994年之後的大部分時間,除1997年,貨幣政策又開始緊縮。如規則要求1998年的利率是_3.6%,而實際的利率卻是4%。
麥卡勒姆規則與泰勒規則比較[5]
麥卡勒姆規則與泰勒規則比較麥卡勒姆規則與泰勒規則的區別在於,操作工具和目標變數的不同。兩種規則中,究竟要選擇哪一種?這依賴於具體的經濟情況。
按照正統的觀點,1995-1998年日本貨幣政策難以刺激經濟,因為利率已經很低。而按照麥卡勒姆規則,基礎貨幣仍處於緊縮過程,表明期間貨幣政策過於緊縮(McCailum,1999,p.9)。
對於美國的貨幣政策,按照泰勒規則,70年代實際利率已經低於規則所擬合的水平;而麥卡勒姆規則表明,70年代貨幣政策過於放鬆,實際基礎貨幣增長高於麥卡勒姆規則所擬合的水平,而且這種差異在1981-1987年有所縮小。這裡,名義GDP增長作為目標變數要比利率規則更有效。
利用泰勒規則對於英國70年代過於放鬆的貨幣政策進行評價,結果表明,建議的政策利率為38%,而當時的實際利率為10.4%。1983-1987年貨幣政策過於緊縮,1987年以來的政策取向是對的。然而,麥卡勒姆規則的解釋則有所不同,70年代的政策過於放鬆,而且直到1990年大多時候仍過於放鬆。
對於日本經濟來說,泰勒規則表明,1972-1974年貨幣政策應該緊縮,而在1982-1987年大多數時候貨幣政策過於緊縮。麥卡勒姆規則表明,90年代中期貨幣政策過於緊縮。
麥卡勒姆(McCallum,2000)用歷史分析方法對60年代初到1998年,美國、英國和日本(日本為70年代初)的貨幣政策決策進行了分析,並使用泰勒規則和麥卡勒姆規則相結合進行分析。對於泰勒規則有許多擴展的形式,包括利用預期未來通貨膨脹代替公式中的實際通貨膨脹。最常見的是,在泰勒規則的右邊加上實際短期利率的滯後變化it − 1,如此得到泰勒規則的變式。
有關貨幣規則的研究表明,各種規則與工具變數有密切關係,反映了規則具有以下基本性能:第一,所採用的規則實際上作為指標變數,而非工具變數。即是說,可以將利率和基礎貨幣變化作為中介目標,而把其他變數作為中央銀行工具的變數進行逐日操作;第二,政策的狀態或松或緊,可由利率或基礎貨幣變化的設定表示,並參照其他變數。
為瞭解決時間不一致問題,貨幣當局需要事先採取規則。這樣,有利於形成公眾預期,一旦規則公開,貨幣當局應該努力達到,否則,貨幣政策的可靠性就會降低。為此,有人建議中央銀行要直接控制基礎貨幣或狹義貨幣,穩定某些可觀察和度量的變數的增長。
中央銀行要控制哪一種工具?麥卡勒姆規則提出,使用基礎貨巾作為隱含工具,名義GDP對現有途徑的偏差可以作為反饋。
托馬斯(1homas,1997,p.325)提出,基礎貨幣是中央銀行資產負債表中的凈貨幣負債。從基礎貨幣的運用來看,包括流通中的貨幣、存款機構在中央銀行的存款;從基礎貨幣的來源來看,具有正的影響包括資產組合、貼現和透支、貨幣發行、黃金儲備和SDR賬戶(特別提款權賬戶)、持有財政發行貨幣;具有負的影響的方麵包括財政在中央銀行的存款、外國和其他機構在中央銀行的存款、財政持有的鈔票以及其他負債和資本。
古德哈特(goodhart,1994)批評把基礎貨幣作為貨幣政策內含工具,基礎貨幣的可行性和合意性是一個處於爭論的問題。不過,在麥卡勒姆規則中,通過利率調整使基礎貨幣增長與所要求的貨幣政策最終目標相配合是有效的。基礎貨幣作為一種信息變數有其吸引力。從概念上看,中央銀行資產在經濟平衡水平中處於重要地位。從實踐來看,在英國,二次世界大戰以後,基礎貨幣流通速度趨勢比較平穩,而且具有可測性。
![\triangle b_1=\alpha-(\frac{1}{16})[x_{t-1}-b_{t-1}-x_{t-17}+b_{t-17}]+\lambda[x^*-x]_{t-1}](/w/images/math/9/f/c/9fcbf34239aa6cd919e09c42d83f8bf2.png) (1)
(1)
霍爾丹、麥卡勒姆和薩門(Haldane,McCallum,andSa]Inon,1996)根據麥卡勒姆規則的如下形式,對英國基礎貨幣的有關規則進行研究:其中,b為基礎貨幣的對數,x為名義GDP的對數,*為目標值。所有數據為季度值。
常數項α為靜態下的名義收入增長,英國的這一值為1%,與名義GDP年增長4%相對應。公式(1)中的第二項為現行的基礎貨幣流通趨勢,其為前4年移動平均值。目的是要考慮較長時期內機構變化的內含。第三項為政策反饋參數,表明GDP偏離其目標值而通過貨幣政策作出反應的速度(取值為0到1)。
對於英國基礎貨幣規則的研究表明,這一規則能夠保證通貨膨脹不高於2%,而且使貨幣政策工具或實際產出易變性更小。這一規則可作為英國現行貨幣政策框架的有益補充,防止貨幣政策出現較大失誤。
克拉克、古德哈特和黃(Clark,Goodhart,and Huang,1999,p.513)提出,在承諾規則和隨意規則的情況下探求最優貨幣政策時,價格和通貨膨脹的持續性是所有菲利普斯曲線實際模型的共同特征。短期內,產出與通貨膨脹之間存在替代性,但就長期來看,經濟本身具有自動恢復穩定的機制。儘管通貨膨脹最終依賴於貨幣存量增長率,產出的短期穩定和通貨膨脹則依賴於實際利率的調整,因為利率可以影響到總需求和產出能力的變化,進而影響到通貨膨脹。
由於通貨膨脹的持續性,承諾規則和隨意規則策略都會導致靜態依存和震動反饋規則,產出的持續性對最優貨幣政策規則具有重要影響。此外,事前預期總是存在於兩種最優貨幣政策規則的替代關係中。考慮承諾規則的政策行動對市場預期的影響,其中只考慮到利率調整對經濟的影響,而沒有考慮到市場對貨幣當局操作規則的反應。承諾規則使預期通貨膨脹接近於通貨膨脹目標,同時,預期產出則遠離其目標水平。對於隨意規則,則相反。隨意規則對於減少隨機震動對通貨膨脹的影響更為有效,因而,隨意規則條件下,隨機震動對產出的影響要比承諾規則更大。
許多人從歷史分析和計量統計得出,貨幣政策對實際產出具有較大影響,實證分析表明貨幣具有非中性的特點。鮑爾和克勞肖(Ball,and Cmushore,1998)對聯邦基金利率作為貨幣政策變化的度量,以專家預測作為預期,結果表明,聯邦基金利率的上升對實際產出要比對預期產出的影響更大,表明經濟主體低估了政策對總需求產生的效應,這樣,貨幣政策的真實效應表現為,對理性預期具有負效應。此外,實際利率的上升會導致隨後2年通貨膨脹的下降,以及幾乎相等的預期通貨膨脹-下降。
對於貨幣政策的實際影響,鮑爾和克勞肖(Ball,and Croushore,1998,p.8)通過實證分析說明,貨幣政策對於實體經濟的影響具有一定時滯,一般來說,貨幣政策緊縮會產生隨後2-3年的通貨膨脹下降,以及隨後1年的產出效應。
赫斯、斯莫爾和佈雷頓(Hess,Small,and Bmyton,1993)提出,麥卡勒姆為了尋求美聯儲能夠直接控制的政策工具,選擇了基礎貨幣作為政策工具。由於經濟學家尚未對巨集觀經濟模型達成共識,需要對不同模型條件下麥卡勒姆規則進行估計,並使樣本更新到1992年。
考慮基礎貨幣作用的以下兩種形式:一是,基礎貨幣直接與支出相聯繫;二是,貨幣傳導機制通過利率運作。由此,得出以下結論:基礎貨幣與名義產出之間的關係看上去有所減弱,主要在於增長的流通速度有較大變化。通過利率進行貨幣政策傳導時,麥卡勒姆的基礎貨幣工具的預測能力與利率對基礎貨幣的敏感度有關,同時短期利率變化通過長期利率進行傳導。這種情況下,對名義收入的可控性較好。最後,有關模型結果表明,使用聯邦基金利率作為政策性工具具有積極的效果。
然而,從歷史上看,基礎貨幣的增長本身不具有穩定性,由於統計原因,以美國的基礎貨幣增長為例進行分析。從1920年1月到1996年4月,以10年為時間單位。每一個10年中,每個月底的12個月基礎貨幣增長從5%到35%不等。10年平均來說,也從0.8%到10%不等(見下表)。
表美國基礎貨幣增長(1920-1996)
| 時期 | 12個月基礎貨幣增長最大值(%) | 12個月基礎貨幣增長最小值(%) | 10年內平均(%) |
| 20年代 | 11.3 | -15.5 | 0.8 |
| 30年代 | 26.6 | -5.7 | 10.0 |
| 40年代 | 25.7 | -9.4 | 10.4 |
| 50年代 | 9.8- | 8.5 | 1.1 |
| 60年代 | 6.9 | 0.4 | 4.2 |
| 70年代 | 9.7 | 5.5 | 7.9 |
| 80年代 | 10.4 | 3.8 | 7.4 |
| 90年代 | 11.4 | 2.1 | 8.0 |
註:有關數據為該年代任何一個時期為12個月基礎貨幣增長的最大值或最小值。
杜克和費歇爾(Dueker,and Fischer,1998)對麥卡勒姆規則進行了考察,結果表明,名義收入反饋規則(nominal feedbaek rules)可以作為貨幣政策的參考指標。







