向量自回歸模型
出自 MBA智库百科(https://wiki.mbalib.com/)
向量自回歸模型(Vector Autoregression, VAR)
目錄 |
向量自回歸模型簡稱VAR模型,是一種常用的計量經濟模型,1980年由克裡斯托弗·西姆斯(Christopher Sims)提出。VAR模型是用模型中所有當期變數對所有變數的若幹滯後變數進行回歸。VAR模型用來估計聯合內生變數的動態關係,而不帶有任何事先約束條件。它是AR模型的推廣,此模型目前已得到廣泛應用。
向量自回歸(VAR)是基於數據的統計性質建立模型,VAR模型把系統中每一個內生變數作為系統中所有內生變數的滯後值的函數來構造模型,從而將單變數自回歸模型推廣到由多元時間序列變數組成的“向量”自回歸模型。VAR模型是處理多個相關經濟指標的分析與預測最容易操作的模型之一,並且在一定的條件下,多元MA和ARMA模型也可轉化成VAR模型,因此近年來VAR模型受到越來越多的經濟工作者的重視。
VAR模型描述在同一樣本期間內的n個變數(內生變數)可以作為它們過去值的線性函數。
一個VAR(p)模型可以寫成為:
其中:c是n × 1常數向量,Ai是n × n矩陣。et是n × 1誤差向量,滿足:
1.例子
一個有兩個變數的VAR(1)模型可以表示為:
或者也可以寫為以下的方程組:
2.轉換VAR(p)為VAR(1)
VAR(p)模型常常可以被改寫為VAR(1)模型。 比如VAR(2)模型:
- yt = c + A1yt − 1 + A2yt − 2 + et
可以轉換成一個VAR(1)模型:
其中I是單位矩陣。
一個結構向量自回歸(Structural VAR)模型可以寫成為:
其中:c0是n × 1常數向量,Bi是n × n矩陣,εt是n × 1誤差向量。
一個有兩個變數的結構VAR(1)可以表示為:
其中:
把結構向量自回歸與B0的逆矩陣相乘:
讓:
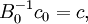
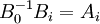 對於
對於 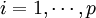 和
和 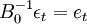
我們得到p-階簡化向量自回歸(Reduced VAR):
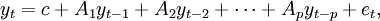
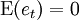 —誤差項的
—誤差項的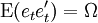 —誤差項的
—誤差項的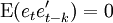 (對於所有不為0的k都滿足)—誤差項不存在自相關
(對於所有不為0的k都滿足)—誤差項不存在自相關
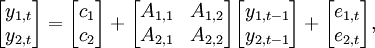
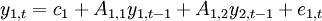
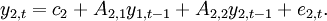
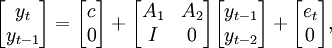
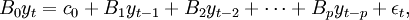
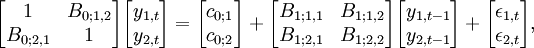
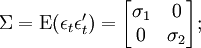
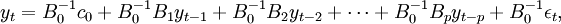









好